从空间维数的本质探讨多体问题下卫星实际运动的轨道
周新力
(湖南邵阳学院 城建系,湖南 邵阳 422000)
1 引言
迄今为止,国内外对卫星运动的基本规律的研究都主要是基于物理学中牛顿的万有引力定律和爱因斯坦的相对论的理论框架所展开的[1-7],并且对于卫星绕地球的运行状态也主要是归因于其受诸多引力作用的结果。在此基础上,对于只考虑地心引力作用的“二体问题”,已基本得到卫星运动的严密分析解;而对于同时考虑其他天体引力作用的“多体问题”,却至今还未得到有效地解决[8-12]。当然,最近几年来国内外一些专家和学者就“多体问题”的算法[13-16]和卫星轨道的测控技术[17-20]这两方面提出了比较好的处理方案。但不管是“二体问题”还是“多体问题”下的卫星运动,其得出的解所描述的只能是一个更接近于卫星实际轨道的运动轨道。本文则是从有别于现有理论框架的另一个新的角度即空间几何的本质来推导的卫星运动的实际的而非近似的轨道方程,供学界参考。
2 问题的提出
从空间的几何性质看,假设朝1维平直方向无限延伸的空间点集为N(N=1,2,…,∞),那么,同时朝2维或3维平直方向无限延伸的空间点集应为N2或N3。相比较可知,尽管在1维、2维和3维等平直空间里的点集都是无限的,但N2的无穷大量总是要比N高一阶,而N3则又是比N2更高一阶的无穷大量。这意味着,假如数量为N2的空间点集不能向2维平直空间无限延伸而只能选择朝某1维平直空间无限延伸,如图1(a)所示,该空间的点集实质上将由N×N变成为1×N2。同样,假如数量为N3的空间点集只能选择朝某2维或1维平直空间无限延伸而不能向3维平直空间无限延伸,如图1(b)所示,该空间的点集实质上也将由N·N·N变成为1·N·N2或1·1·N3。
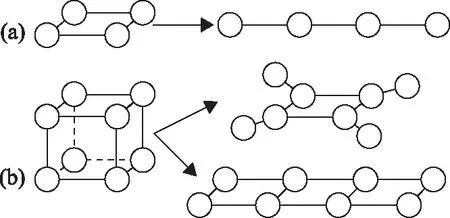
图1 高维空间的点集到低维空间的几何映射
值得注意的问题是,由于朝任何一个平直的方向无限延伸的宇宙空间其相互垂直的平直的几何维度最多只有3个。假设在宇宙空间里建立一个3维直角坐标系o-xyz,对于数量为Nn(n≥4)的空间点集,如图2(a)所示,尽管它既可以选择全部都在1维的平直空间o-y内无限延伸,又可以选择部分在o-y之外沿2维平直空间o-yz的z方向分布的其他1维平直空间zi-y(i=1,2,3,…)内无限延伸,或者还可以选择部分在o-yz之外沿3维平直空间o-xyz的x方向分布的其他2维平直空间xi-yz(i=1,2,3,…)内无限延伸;但事实上却不能进一步选择向o-xyz之外沿4维或4维以上方向分布的另外3维平直空间内无限延伸,如图2(b)所示。这就决定了数量为Nn(n≥4)的宇宙空间里所有点集在本质上为3维的平直的无限延伸的立体几何空间里分布时,只能重叠在3维空间的各个点上而发生变化,即由N·N·N·N·…·N变成为Ni·Nj·Nn-i-j·1·…·1(i,j 图2 4维或4维以上空间与3维空间的几何性质的差异 若把静止于3维直角坐标轴上的点集定为0阶,则在该3维直角坐标系上任意标准时刻t的瞬间某一个区域空间V内的点集实质上应包括0-n阶。假设用(x,y,z)t代表空间位置点0阶的3维直角坐标值,然后用(x(1),y(1),z(1))t、(x(2),y(2),z(2))t、……、(x(n),y(n),z(n))t等分别表示空间位置点的匀速变化、匀加速变化、……、匀变变加速变化的各阶3维直角坐标值,那么,在任意时刻t该区域空间V的体积大小实质上应为 (1) 图3 空间维数的几何本质 (2) 从式(2)可以看出,只有当A点的空间位置变化的速度、加速度和变加速度等各阶坐标值在任意时刻均为零时,o点到A点的空间距离soA才是3维直角坐标系o-xyz空间里的两个坐标位置点之间的几何空间距离loA,该值始终是一个固定不变的定值。而当A点的任意一阶位置变化的坐标值在某一时刻t1不为零时,soA实际上是一段4维或4维以上的空间里两个点之间的几何空间距离,该值是随时间而不断变化的。宇宙空间内任意两个质点,只有当两者相对静止时,才共同处在一个3维或3维以下的空间里;而当它们相对运动时,实质上是处在一个4维或4维以上的高维空间里。这也意味着,当用电磁波测量o点与A点之间的空间距离时,有一点可以肯定的是,假设以坐标系o-xyz空间的时间为标准,那么,电磁波在t1时刻无论是由o点发出还是由A点发出,在t2时刻到达对方时,它实际所覆盖的空间距离的理论值应该为soA而绝不是loA。 空间维数的本质和空间距离的本质说明,对于宇宙空间里任意一个物体或质点,其静止时的位置和运动时的轨道,都可以直接使用3维位置坐标和各阶位置变化的运动坐标来正确地描述之。假设以地球为静止参照系建立一个以地球的质心Q为原点、以地球自转轴为Z轴、固联在地球上并随地球自转的3维直角坐标系Q-XYZ,并设t时刻卫星j在该坐标系上的位置坐标为(xj,yj,zj)t,由于卫星和地球、月球等都在同一个地球公转的轨道面上,即它们在太阳系这一阶空间的阶数(假设为n)是一致的,则t时刻该卫星的位置变化的速度、加速度和变加速度等各阶坐标值C(1)~C(n)在Q-XYZ上的3个分量分别为 对于卫星在太空中运动的实际轨道实质上可以通过直接使用3维位置坐标和各阶位置变化的运动坐标来建立一个类似泰勒展开式的运动方程予以正确地描述,即 (3) 其中 (4) 卫星中心与地心之间的空间距离的理论值为 (5) 根据以上的卫星运动方程可以得出这样一个观点:即假设卫星仅仅受地球引力的作用而作圆周运动时的运动方程为 x=Ssinωt,y=Scosωt,z=0 若将此方程化为式(3)的形式,即 则该方程意味着,通常所认为的“卫星围绕地球作圆周运动是地球引力作用的结果”实质上可以理解为卫星的运动并不是什么引力的作用,而仅仅是因为它处在一个以地球为中心的高维空间里的某一个点上,该点在以地心为原点的坐标系上的空间坐标分别为 同样,对于所谓的“卫星在多体问题下的自由运动(即无人为作用的运动)”,实质上也可以理解为“卫星并没有受到地球、太阳和月亮等诸多引力的作用而运动,只是因为它处在地球围绕太阳公转的这一阶高维空间里的某一个点上,该点在以地心为原点的坐标系上的空间坐标分别为 (6) 图4 卫星的几何定轨原理——距离交会法 当将式(6)的计算结果代入式(3)和式(4)的卫星运动方程后,则进一步可以解算出这个卫星在任意ti时刻的空间位置3维坐标值(x,y,z)ti和空间位置变化的k阶3维坐标值(x(1),y(1),z(1),x(2),y(2), [1] 刘林.人造地球卫星轨道力学[M].北京:高等教育出版社,1992. [2] 爱因斯坦.狭义和广义相对论浅说[M].杨润殷,译.北京:北京大学出版社,2006. [3] 吴连大,王昌彬,童傅.人造卫星二阶摄动理论的半分析半数值方法[J].天文学报,1978,19(2):131-150. [4] 柳响林,PAVEL D.基于B-spline和正则化算法的低轨卫星轨道平滑[J].地球物理学报,2006,49(1):99-104. [5] RUSSEL R P,LARA M.Long-lifetime Lunar Repeat Ground Track Orbits[J].Journal of Guidance,Control and Dynamics,2007,30(4):982- 993. [6] 毛悦,宋小勇,贾小林.GEO/IGSO/MEO卫星轨道根数演化分析[J].测绘科学,2009,34(1):119-121. [7] 罗志才,钟波,宁津生,等.GOCE卫星轨道摄动的数值模拟与分析[J].武汉大学学报:信息科学版,2009,34(7):757-760. [8] 冯来平,贾小林,吴显兵,等.一种基于抗差M估计和动力学平滑的卫星轨道综合方法[J].中国科学G辑,2010,40(5):603-607. [9] 冯晶琅,袁建平,陈记争.不同高度范围月球卫星轨道受摄分析[J].西北工业大学学报,2011,29(2):194-197. [10] 童科伟,刘伟,高朝辉,等.月球卫星轨道摄动及冻结轨道研究[J].航天器工程,2012,21(2):12-17. [11] 刘大杰,施一民,过静珺.全球定位系统(GPS)的原理与数据处理[M].上海:同济大学出版社,2001:97-102. [12] MARCHAL C,孙义燧.多体问题中惯量矩的演变[J].中国科学A辑,1985(6):557-565. [13] LUK’YANOVL G L,NASONOVA P,SHIRMIN G I.The Lagrange-Jacobi Equation in the Finite-size Many-body Problem[J].Astronomy Letters,2003,29(9):635-639. [14] GUILLOT A.The Painlevé Property for Quasihomogenous Systems and a Many-body Problem in the Plane[J].Communications in Mathematical Physics,2005,260(1):181-194. [15] 梁雨婷,谭毅,程楠,等.一种混合算法求解多体问题下行星际转移轨道[J].计算机与数字工程,2010,38(4):15-29. [16] 李琪刚,柴亚辉,徐炜民,等.多体问题FMM 算法在加速部件FPGA 研究与实现[J].计算机工程与设计,2011,32(10):3391-3394. [17] 刘丽丽,文浩,金栋平,等.绳系卫星轨道转移的最优控制[J].航空学报,2009,30(2):332-336. [18] 李恒年,李济生,黄永宣.动力学补偿受控卫星轨道确定算法[J].宇航学报,2010,31(10):2269-2275. [19] 耿涛,刘经南,赵齐乐,等.星地监测网下的北斗导航卫星轨道确定[J].测绘学报,2011(增刊):46-51. [20] 陈明,张宇,曹建峰,等.嫦娥二号卫星轨道确定与测轨技术[J].科学通报,2012,57(9):689-696.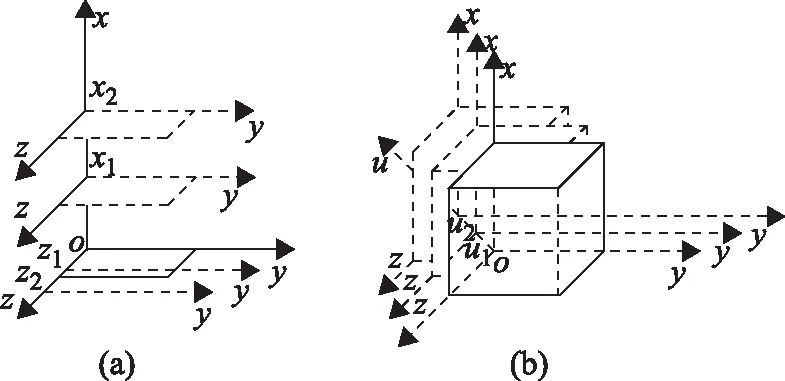
3 理论依据的分析
3.1 空间维数的本质

3.2 空间距离的本质



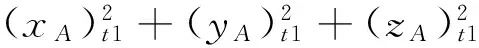

4 探讨的结果
4.1 卫星在太空中的运动轨道方程
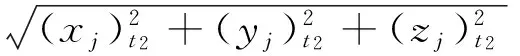
4.2 方程的意义
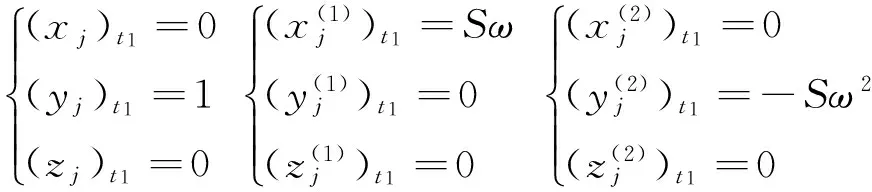
5 结束语




