一种流量可调燃气发生器压强控制算法的研究①

刘源翔，姚晓先，聂聆聪，宋晓东

(1．北京理工大学宇航学院，北京 100081;2．中国航天科工集团公司三十一所，北京 100074)

0 引言

新一代超声速巡航导弹追求大机动、宽空域飞行，但以冲压方式进入固体火箭冲压发动机补燃室的空气流量会随飞行高度、马赫数及攻角等飞行条件的变化而变化，发动机性能也会随之变化［1－3］。同时，为提高导弹的机动性和灵活性，要求发动机推力在一定范围内能够连续可调。因此，为保证发动机具有最佳的工作性能和良好的推力调节能力，必须对燃气发生器产生的燃气流量进行调节［4］。用于燃气流量调节方案主要有2种:改变燃气发生器喷喉面积的调节方式;喷管的自适应调节。目前，采用燃速对压力敏感的推进剂，利用机械阀门改变燃气发生器喷喉面积来控制燃气发生器内压强，进而控制燃气流量的方法是较为理想的选择［5］。美国、俄罗斯、德国、加拿大等国针对固体火箭冲压发动机燃气流量调节技术展开了大量的研究［6－8］，其中欧洲导弹公司 MBDA 研制的“Meteor”导弹采用了滑环阀［9］。国内也对此项技术积极开展工作，包括对流量调节阀形状的讨论与设计［10－11］、流量调节系统的建模以及动态特性的分析等［12－13］。但在导弹飞行过程中，燃气流量不可测量，无法对流量实现直接控制，普遍采用对燃烧室内压强控制的方法，以达到对燃气流量的调节。

目前针对燃气发生器的压强系统模型分析及控制算法研究较少。本文建立了燃气发生器压强控制系统的模型，对系统稳态与动态进行了分析，讨论了模型的变量因素以及这些因素对系统参数的影响。基于这些分析结果提出了一种前馈自适应PID控制算法对燃烧压强进行控制，并与传统算法进行比较。

1 燃气发生器模型分析

流量可调燃气发生器采用柱型装药方式，工作时为端面燃烧，推进剂燃速对压强敏感，且满足燃速公式r=apcn。

1．1 稳态模型分析

当燃气发生器内压强处于稳定状态时，燃气发生器喉道面积保持不变，燃气生成量与喷口的排出量相等:

其中，燃气生成量mp=ρprAb，燃气排出量mg=pc0At0/C*，则可得到稳态时燃烧室压强:

式中 ρp为推进剂密度;Ab为燃烧药柱面积;a为燃速系数;At0为当前燃气发生器喉道面积;C*为推进剂特征速度;n为压强指数;pc0为当前燃烧室内压强。

以某燃气发生器为例，稳态时燃烧室内压强随喉道面积变化的曲线如图1所示。从式(3)与图1可知，燃气发生器稳态模型为非线性模型，推进剂确定后，压强指数n为常值，燃烧室稳态压强随喉道面积增大而减小。

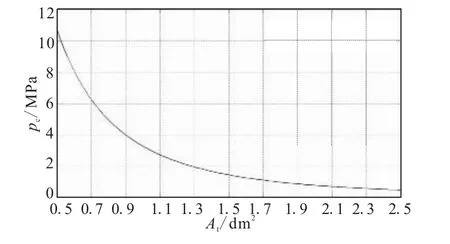
图1 稳态时压强随喉道面积变化曲线Fig．1 Relationship between pressure and gas control valve area at steady state

1．2 动态模型分析

不考虑起始燃烧状态、燃烧初温以及压强分布等非主要因素的影响，燃烧室压强可近似为零维压强，满足式(4)的零维弹道方程［14］:

式中 Γ为比热容比函数;Vg为燃气发生器内的自由容积。

由式(3)可知，在动态过程中，燃烧室压强与喉道面积为非线性关系，需对其进行线性化处理。将式(3)在某平衡位置小偏差线性化后可得

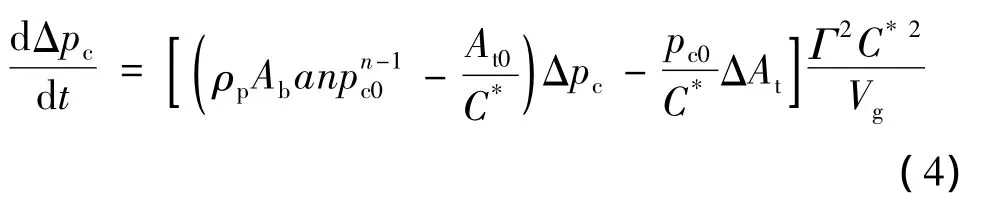
引入相对偏差量 ΔA=ΔAt/At0，Δp= Δpc/pc0，并对其进行拉普拉斯变换，则为

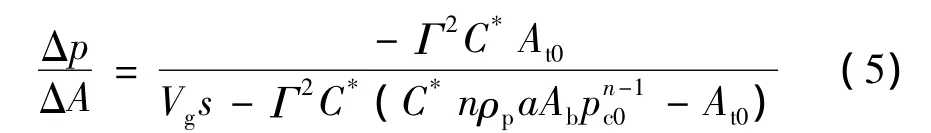
将式(6)写为零极点形式，得到压强关于面积线性化后的传递函数为

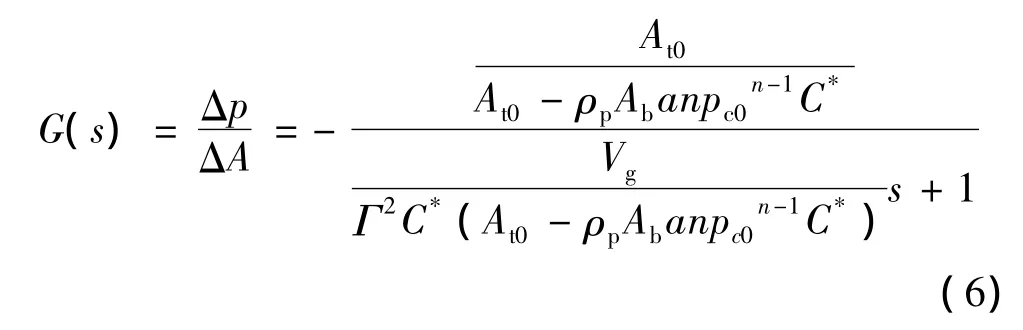
式(7)即为燃气发生器内压强在某个平衡点位置关于喷喉面积的小偏差线性化模型。令:

则模型为

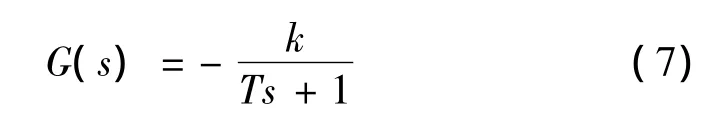
式中 T为系统时间常数，与At0、pc0及Vg有关;k为系统增益，与At0和pc0有关。

从上面分析可看出，T和k随系统状态变化而改变。以某燃气发生器的燃烧药剂测试试验为例，取如下几个特征点的状态量，计算当前的系统参数。其中起始段为燃气发生器点火开始燃烧，喉道保持最大，燃烧室压强达到稳定后的时段;上升段为调节阀运动，喉道收缩，压强开始上升但是未达到平衡的时段;稳定段为调节阀达到目标位置，喉道不变，压强保持平稳状态的时段;下降段为调节阀继续运动，喉道扩张，压强开始下降的时段;结束段为调节阀停止运动，喉道达到最大，压强处于平稳的时段。

最终得到各项参数及计算数据，如表1所示。上升阶段与起始阶段相比，自由容积与压强变化不大，喉道面积减小90 cm2，上升阶段的系统的时间常数增大了约1倍，系统增益也增大15%;下降阶段与上升阶段相比，喉道面积基本不变，自由容积与压强增大，下降阶段时间常数基本不变，系统增益则减小了约25%。

分析表明燃气发生器动态工作过程模型可近似为时间常数和增益摄动的一阶惯性系统。

表1 系统参数随状态变量变化关系Table 1 Relationship between system parameters and state variable

2 压强控制器的设计

根据以上的模型分析，燃气发生器是一个具有变参数的非线性系统，同时在工作过程中存在喉道不完全密封、调节阀烧蚀及燃烧颗粒沉积等干扰因素，采用普通的PID控制器难以满足控制精度及响应速度的要求。这要求在控制系统中存在一个参数调节器，能参考系统的状态量，实时对控制参数进行修正，以适应控制对象的状态变化。

2．1 参数变化规律分析

为了对压强控制器进行设计，必须找出燃气发生器系统模型参数随状态量变化的规律，并根据变化规律及状态量对系统参数的影响程度，来选择控制器所参考的状态量及控制参数的变化规律。

根据式(7)，可分别获得T与k关于Vg、At0和pc0的变化曲线，如图2～图4所示。由图2可见，T与Vg成正比。

图2 时间常数随自由容积变化曲线Fig．2 Relationship between time constant and free volume of gas generator

T、k与At0之间是一种非线性关系，均随喉道面积的增大而减小，且随着喉道面积越大，单位喉道面积变化引起T与k的变化也越小，如图3所示。T、k随着pc0的增大而减小，并且从整体来看，单位压强变化引起的时间常数与增益的变化比较小，如图4所示。

图3 时间常数、增益随喉道面积变化曲线Fig．3 Relationship between time constant，gain and control valve area

图4 时间常数、增益随燃烧室压强变化曲线Fig．4 Relationship between time constant，gain and pressure of gas generator

2．2 参考量的选择及控制算法提出

根据2．1节的分析可知，对T与k影响的状态量包括Vg、At0和pc0。其中，Vg对 T的影响较大，因此需要将其作为参数调节器所要参考的因素。At0的变化对T与k造成一定的影响。而在实际工作过程中，喉道面积作为控制执行的变量，其变化的速度及大小都直接由控制器计算得出，从而不需要将面积反馈作为参数调节器的参考因素。pc0对T与k的影响较小。但是在对稳态模型分析中可知，稳态时喉道面积决定着燃烧室内的压强，并且压强越高，单位喉道面积的变化所引起的压强波动越大，因此在控制器的设计中，需要将压强反馈量作为一种参考因素来控制喉道面积的变化速度。

综合上述分析，参数调节器中需要参考的状态变量为Vg及pc0。其中Vg为一不可逆的变量，在实验过程中一直增长，时间常数也随之变大。因此控制参数调节器需要随着Vg的增大而改变控制器参数值，以减缓控制速度，进而减小系统的超调量，提高系统精度。在燃气发生器工作在稳态时，pc0越大，单位喉道面积引起的压强变化也越大。所以随着燃烧室内压强的上升，控制参数调节器需要改变控制器参数值，以减小喉道面积变化速度，使系统保持稳定。

自由容积在实际实验中无法直接测量，而在动态过程中，它满足方程(8)的等式［15］，通过对方程(8)右边积分可间接得到当前的自由容积值。

对稳态模型分析可知，无论之前动态过程如何，当喉道面积确定时，燃气发生器内总会有一个压强值与当前喉道对应。因此，在控制中引入前馈通道，将目标压强值经过理论计算，得到理想的喉道面积值，参与对压强的控制。

根据上述的分析，提出一种前馈自适应PID控制方案，其中自适应PID部分参考当前的pc0与Vg选择适当的控制器参数，对压强误差进行计算控制，增强系统的鲁棒性;前馈部分直接对目标压强信号进行计算，提高系统对目标信号的响应速度。

控制框图如图5所示。在图5中Atc为输出给执行机构的控制指令，它主要由2部分组成:一部分由目标压强信号经过理论计算得到，跟其他因素无关;另一部分则是目标压强与反馈压强的压强误差经过压强控制器计算得到。其中控制器参数值由调节器参考Vg及pc0选择得出。

图5 燃气发生器压强控制框图Fig．5 Control diagram of pressure for gas generator

3 仿真比较实验与结果分析

假定推进剂参数如下:C*=750，n=0．5，Ab=2．7×10－2，ρp=1 600，a=5．9 ×10－6，Γ =1．1，燃烧室内的初始自由容积为0．002 m3。同时为减小过程中逆响应的作用，输入控制信号采用梯形波信号［16］，每个梯形波信号上升时间与下降时间都为3 s，持续16 s，仿真时间共为100 s。

在上述条件下，分别采用前馈自适应PID控制器与传统的PID控制器对燃气发生器进行控制。

图6为在不同控制器作用下，燃烧室压强随控制信号变化曲线。在实验的开始上升阶段，2种控制器的跟随性能基本一样，其中采用PID控制器的系统略微出现一点超调。随着燃烧的进行，自由容积慢慢增大，T也随着改变，采用PID控制的系统曲线超调量增大，第2个波形时达到了8．3%，同时在稳态时产生了波动。随着时间推移，超调量越来越大，第3个波形时，超调量更是达到了15%。

在梯形波的下降阶段，燃烧室压强变小，单位面积变化引起的压强变化也开始变小，采用PID控制器的系统响应速度在下降阶段变慢，调节时间达到了4．7 s。而前馈自适应PID控制器根据系统参数变化实时调节控制参数，并且前馈的存在能有效地响应控制信号的变化，使系统具有很好的跟随特性与控制精度。在上升阶段中，燃烧室内压强几乎没有超调，平稳地达到目标压强。而在下降段，燃烧室压强很好地跟随目标压强，快速降下来，调节时间只是很小的0．8 s。采用前馈自适应PID控制器的控制效果明显优于传统的PID控制方式。

图7为在不同控制器作用下，燃气流量随控制信号变化曲线。从图7看出，由于压强的波动，采用传统PID控制器的系统燃气流量随着压强波动比较大，而采用前馈自适应PID控制器的系统对燃气流量的调节速度快、波动小、控制精度高，能够更加快速地响应冲压发动机中空气流量的变化，有效地保证发动机的稳定工作。

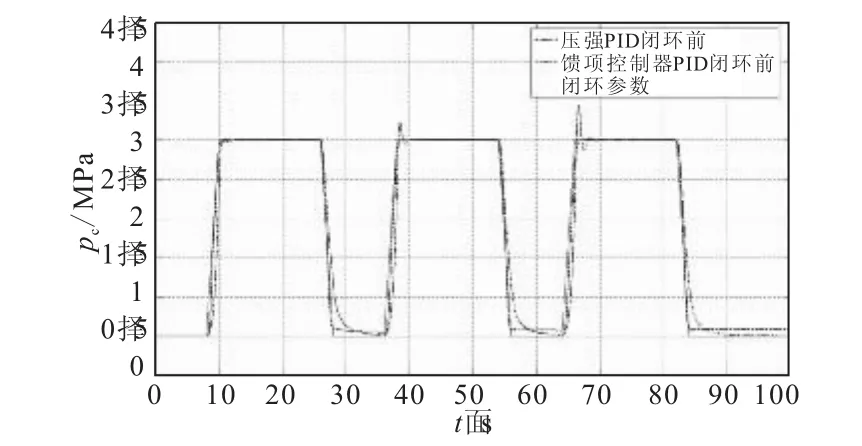
图6 压强响应曲线Fig．6 Response of pressure

图7 燃气流量响应曲线Fig．7 Response of mass flow rate

4 结论

(1)燃气发生器压强变化模型线性化后为一个参数摄动的一阶惯性系统，并且其参数跟自由容积、喉道面积及当前压强有关。

(2)本文分析了动态模型中变量对系统参数的影响，并结合系统的稳态模型特点，提出一种前馈自适应PID控制方案，有效克服了系统参数摄动对控制带来的影响，提高了系统的响应速度与控制精度。

［1］ Besser H L．Development testing of throtteable ducted rockets［M］．Air-breathing Propulsion for Missiles and Projectiles，1992:1-13．

［2］ Wilson R，Limage C，Hewitt P．The evolution of ramjet missile propulsion in the U S and where we are headed［R］．AIAA 96-3148．

［3］ 鲍福廷，黄熙君，张振鹏．固体火箭冲压组合发动机［M］．北京:宇航出版社，2006．

［4］ 王志吉，夏智勋，罗振兵，等．固体火箭冲压发动机燃气流量调节技术研究［C］//中国复合材料学会教育与科普委员会2001年学术研讨会论文集．北京:中国航空学会，2001:169-170．

［5］ 马立坤，夏智勋，胡建新．阀门作动速度对流量可调固体火箭冲压发动机动态响应特性的影响［J］．导弹与航天运载技术，2012(2):8-13．

［6］ Wikerson F S，Lucas J T．Variable flow solid propellant gas generator for missile control systems［R］．AIAA 81-1464．

［7］ MillerW H，BurkesWM J R，Mcclendon S E．Design approaches for variable flow ducted rocket［R］．AIAA 81-1489．

［8］ Christoph Bauer，Francois Davenne，Norman Hopfe．Modeling of a throttleable ducted rocket propulsion system［R］．AIAA 2011-5610．

［9］ 谷满仓，熊本炎，张雅凤，等．欧洲流星超视距空空导弹的研发历程［J］．飞航导弹，2012(7):18-22．

［10］ 候晓静，莫展．固冲发动机燃气流量调节阀设计与调节特性研究［J］．弹箭与制导学报，2011，31(2):123-126．

［11］ 兰飞强，王丽娟，程翔，等．一种固冲发动机用流量调节装置设计［J］．弹箭与制导学报，2012，32(3):148-151

［12］ 鲍文，牛文玉，陈林泉，等．固体火箭冲压发动机燃气流量调节特性［J］．推进技术，2007，28(4):433-436．

［13］ 聂聆聪，姚晓先，等．固体火箭冲压发动机燃气发生器的最优流量控制算法研究［C］//2011年中国宇航学会固体火箭推进暨航天第三专业信息网学术交流会论文集．2011:665-673．

［14］ 段丽华．某伺服系统燃气发生器及调压阀的动态仿真研究［J］．航空兵器，2005(12):38-42．

［15］ 何洪庆，陈旭扬，孙贵宁．固冲发动机的流量调节技术——流量调节系统设计［J］．战术导弹技术，2009(2):36-40．

［16］ 杨石林，高波，董新刚．滑盘式流量调节燃气发生器动态特性分析［J］．固体火箭技术，2009，32(5):506-510．