低空高速飞行器整流罩分离技术研究现状和展望①

朱学昌，李浩远，喻天翔，宋笔锋

(1．西北工业大学 航空学院，西安 710072;2．北京宇航系统工程研究所，北京 100076)

0 引言

当运载火箭/导弹在大气中飞行时，整流罩用于保护卫星、弹体及其他有效载荷，以防止卫星受到气动力、气动加热及声振等有害环境的影响，是运载火箭的重要组成部分。当火箭或导弹飞行到一定高度时，必须及时将整流罩分离并抛弃，以便有效载荷正常工作和减轻飞行器的后续质量，使飞行器的作用得到有效发挥。整流罩分离能否成功，直接影响飞行任务的成败，航天发展史上因整流罩分离失败导致飞行失败的案例不少，最近的一次在2011年3月4日，美国轨道科学公司用金牛火箭发射气象卫星就是因为整流罩分离失败而导致发射失败［1］，这是继2009年同样原因的第二次失败［2］。

整流罩分离技术可分为分离方案和分离过程计算。分离方案是针对不同环境、不同任务的运载器设计适合的整流罩构型和分离方式;分离过程计算是通过地面试验或仿真，获得整流罩分离轨迹、弹性变形及分离参数等，以保证分离运动的安全。

长期以来，随着航天技术和弹道导弹技术的成熟，各国对太空的探索活动日益频繁。另外，随着导弹对机动、突防等功能的要求，特殊弹道的研究日益活跃，尤其是低弹道导弹能够实现一些常规弹道难以实现的目标，其优势逐渐显现出来。随着任务要求的提高，火箭或导弹的整流罩也需要更深层次的研究与突破。整流罩分离技术作为运载器能否完成任务的关键点，因此引起了广泛关注。

本文对目前整流罩各种分离方式的优缺点进行分析，找出适合低空高速下分离的方式，并分析低空高速整流罩分离技术的特点以及技术涉及的研究内容。

1 整流罩类型及分离方式分析

1．1 整流罩结构类型

根据运载器的任务不同，整流罩的类型及分离方式各异。导弹、火箭高速飞行器整流罩，根据结构外形主要分为圆锥形、圆锥－圆柱形和圆锥－圆柱－倒锥形，如图1所示。

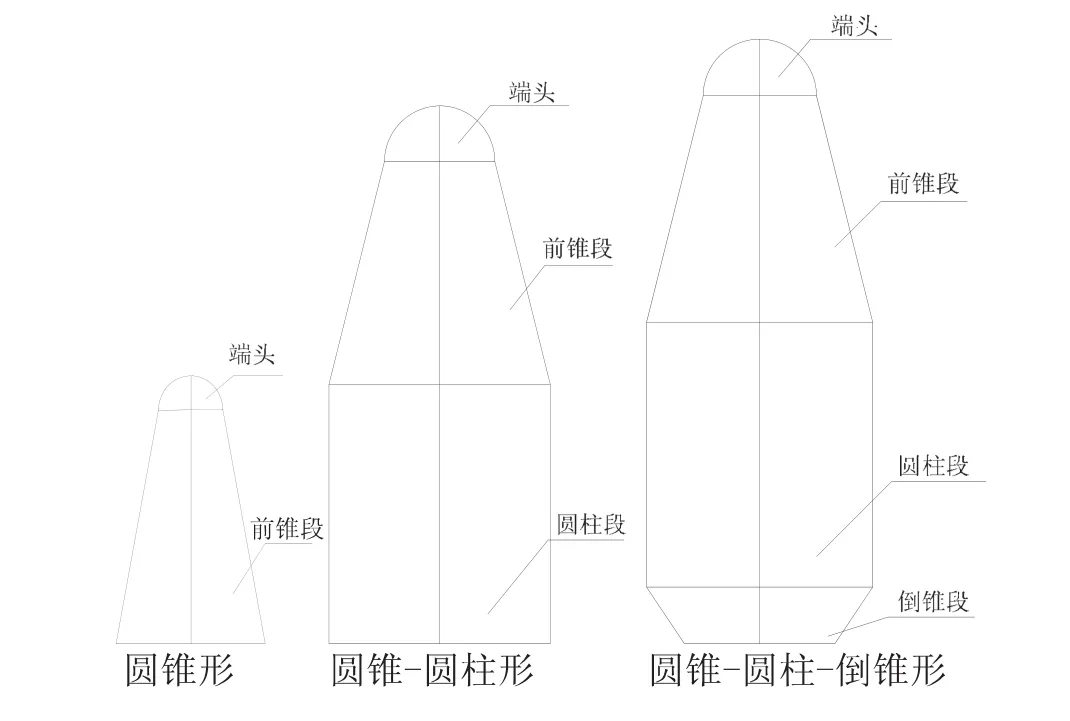
图1 整流罩的结构外形Fig．1 Fairing structural shape

在火箭(或导弹)直径相同的情况下，3种整流罩的对比情况如下:

(1)圆锥形整流罩一般比较短小，整流罩内有效载荷小、仪器设备少，整流罩下端直径与火箭和导弹的直径相同，气动特性好。

(2)圆锥－圆柱形整流罩比圆锥形整流罩大，其内的有效载荷和仪器设备较多，用于火箭(或导弹)直径与整流罩直径相同的情况，气动特性较好。

(3)圆锥－圆柱－倒锥形整流罩大，整流罩内有效载荷大、仪器设备多，整流罩外径比火箭(或导弹)直径大，这种整流罩由于有倒锥，气动特性复杂。

随着生产技术水平的提高，锥－柱的过渡方式可由渐变的方式取代，如母线渐变的卡门头部、西尔斯－哈克旋成体前半部［3］等，这样的整流罩阻力更小，能提高运载能力。

1．2 整流罩分离方式

目前，国内外火箭、导弹等飞行器分离整流罩分离方式有整体拔罩分离、两瓣旋转分离、两瓣平推分离、多瓣旋转分离和多瓣平推分离等方式。

(1)整体拔罩分离。整流罩与运载器横向解锁后，将整流罩向前推，使整流罩拔出，然后再使整流罩侧向运动偏离火箭飞行轨道［4］。这种分离方式的优点是分离过程中整流罩为一整体，刚度好，变形小;缺点是分离相对运动距离长，需要导向，而且需要在整流罩上安装固体小火箭以提供分离力。对于锥－柱－锥形整流罩不适用。在低空高速下分离时，整流罩受到的气动阻力和干扰力较大，应用受到一定的限制。

(2)两瓣旋转分离。整流罩先沿横向与运载器解锁，然后纵向解锁成2个半罩，在推力(如弹簧力)作用下，每个半罩绕其与箭体的连接铰链旋转到一定角度后，整流罩与铰链脱钩，并向外运动，完成与运载器的分离［5－10］。该分离方式的优点是需要的分离推力比较小，整流罩与运载器的分离距离小，分离过程中有铰链限位，一般不会与运载器碰撞，适用的范围比较广;缺点是需要进行横向和纵向2次解锁，需要设置铰链，而且需要比较多的弹簧提供分离力，机械结构比较复杂。现大型火箭多采用此类分离方式。在低空高速下分离时，气动力可作为分离的部分动力。

(3)两瓣平推分离。该方式也是将整流罩先沿横向与运载器解锁，然后纵向解锁成2个半罩，之后两半罩在推力作用下平动，远离运载器，实现整流罩分离［11］。该方式的优点是无需铰链和固体小火箭，结构相对简单;缺点是分离过程中2个半罩运动不受控，半罩姿态变化大，可能与运载器碰撞，一般只适用于高空、气动力可忽略的情况。例如长征二号E火箭，其整流罩分离采用“平移－翻转”方式，2个半罩分离后先向外平移15 mm，然后绕铰链旋转分离，两半罩的分离解锁用导爆索线性分离装置，弹簧提供分离初始旋转力矩，用限位销控制平移距离，分离外界为真空。

(4)多瓣旋转分离与两瓣旋转分离类似，只是整流罩解锁后分解成多瓣而不是两瓣;多瓣平推分离也与两瓣平推分离类似［12－13］。

综上所述，旋转分离方式由于在分离初期有运动限位机构，且气动力可作为部分分离动力，比较适合用于低空高速下的整流罩分离。

1．3 低空高速整流罩分离技术特点和研究内容

低空高速整流罩分离运动相比于目前运载火箭、导弹等高空高速或低空低速分离运动［14－16］最大的区别在于面临来流空气的高动压，气动力的影响占主导地位。故低空高速飞行器整流罩的分离过程涉及空气动力学及流固耦合等问题，更加复杂。目前，低空高速整流罩分离技术研究主要分三方面:

(1)稠密大气层内高马赫数的整流罩分离流场计算。相对于高空整流罩分离运动，低空分离中空气动力与现在推力装置提供的确定推力不同，它与分离时火箭攻角、飞行速度、整流罩内有效载荷形状等因素密切相关，变化范围大，且试验条件难以模拟，数值计算困难。

(2)低空环境巨大的气动力使罩体结构变形。大型整流罩为薄壁壳结构，整流罩分离过程中弹性变形大，整流罩与其内有效载荷间的间隙小，弹性变形会减小此间隙，从而影响分离，因此分离过程必须考虑整流罩在各种载荷作用下的弹性变形。

(3)流场－运动－变形一体化耦合分析。整流罩分离高度降低后，空气动力成为主要的分离推动力。流场－运动－变形一体化耦合分析将是后续整流罩分离必须解决的问题，是分析研究的趋势。

2 整流罩分离关键技术及其发展

2．1 整流罩抛罩流场计算问题

整流罩抛罩属于流体与刚体运动及二者互相耦合的复杂问题，同类的问题还有飞机外挂物的投放，飞机座舱盖的抛离，火箭级间分离、飞机弹射救生等。这类主要由气动力决定的分离过程，具有马赫数高、动压大、迎风面积大、质量轻等特点，流动呈现高度非定常和非线性复杂特征并伴随着多体间强相互干扰，无论是理论分析、风洞试验或数值计算，准确预计整流罩分离运动都有一定难度，给空气动力学研究带来新的难题。

针对此类运动的流场分析求解，目前国内外一般采用以风洞试验和飞行试验为主的试验方法和数值计算方法。在此类问题的实验研究中除了马赫数、几何外形等空气动力学相似条件外，还需要满足Froude相似律、重定律或轻定律等运动特性相似条件，因此试验条件和模型设计非常苛刻［17］，这使得国内外把目光投在计算流体力学，开展研究此类问题。

地面风洞实验主要有非定常流动确定模型运动特性的自由飞实验以及定常流动确定模型运动特性的可控轨迹系统(Captive Trajectory Support，CTS)实验，而相对运动的多体动力学系统流动数值模拟常用的方法有类似于CTS试验的准定常计算方法和直接模拟非定常流动特性的计算方法。1997年，美国对飞机投放外挂物研究发现［18］，计算模拟得到的气动力预测飞行轨迹，比CTS试验更接近飞行试验弹道，主要原因是采用准定常假设的CTS试验未能反映流动非定常特性。基于这种认识，美国很重视发展数值模拟和飞行试验技术。

国内从20世纪90年代后期开始，大部分研究采用基于重叠网格技术的准定常计算方法，近几年国外探讨分离过程主流是发展动网格技术。动网格技术有非结构动网格技术(Dynamic Unstructured Method，DUM)和杂交重叠网格(Chimera Grid Method，CGM)。CGM通过相对运动的子块网格来实现飞行物体之间相对运动，每一个块内网格可以采用较为成熟的网格技术，生成以后网格点之间相对静止;CGM计算效率稍高，但是每一步需要处理相对运动引起的块与块之间的信息交换，频繁的插值将带来误差传递和累积;另外对于包含激波的流动，线性插值限制了计算精度的提高。国内杨爱明等模拟直升机前飞旋翼［19］、刘鑫等对重叠网格预处理的研究［20］、李孝伟等数值模拟飞机外挂物投放［21］，另外还有北京空气动力研究所纪楚群、张玉东等［22］、南京航天航空大学招启军、徐国华等［23］都采用CGM取得了较好成果。DUM采用网格变形来描述物体的相对运动，近几年南京航空大学的伍贻兆［24］和气动中心张来平［25］采用结构网格/非结构网格相结合的研究路线，该方法在仿真计算中应用很多［26－28］。常用的网格变形模型有弹簧近似(Spring Analogy)模型、弹性体(Elasticity Method)模型和代数模型。国防科大的郭正［29］对标准弹簧近似模型进行改进，加入表示扭转弹簧效应的修正因子，使网格边扭转受到约束，克服了标准弹簧近似方法在二维或三维扭曲最严重时出现的网格边互相交叉，避免了频繁的局部重构，取得了很好效果。

结构网格优点是技术成熟，网格拓扑结构简单，流场计算精度高，边界处理能力强;其缺点是几何形状复杂的计算区与网格划分不够灵活。非结构网格最大的优点是划分简单，网格划分周期短。在整流罩分离计算中，应根据整流罩尺寸、罩内有效载荷的几何外形、所处工况以及分离方式和分离载荷来确定流场计算分析方法，以获得较为准确的气动载荷条件。

2．2 整流罩分离安全问题

整流罩分离后罩体分散开来，罩体运动轨迹可能与运载器的飞行轨迹产生干涉，影响任务安全。在目前的研究中，整流罩分离的可靠性是研究的热点。Anandhanarayanan K等［30］在导弹分离动力学研究中提到抛罩等研究首要任务就是保证安全，并提出分离运动的类比性研究方法和初步的分离可靠性研究进展。张永杰等［31］针对整体式整流罩采用最小二乘法拟合罩体运动轨迹，利用蒙特卡罗法计算罩体运动的可靠度。整流罩分离运动涉及流体力学、固体力学等多学科，Melike Nikbay等［32］在研究气弹系统时提出基于可靠性的多领域结合设计优化方法，解决结构和气动力的不确定性，给整流罩分离运动的可靠性研究提供了方法。

此外，在低空高速下气动力较大，薄壁结构的整流罩会发生较大的弹性变形，由此将减小整流罩与罩内有效载荷的安全间隙，严重时会导致毁伤有效载荷。整流罩在复杂气动力作用下的弹性变形涉及到气动特性和结构动特性，分析计算复杂，目前开展大气动力与结构弹性变形研究的还不多。

2．3 分离过程动力学问题及仿真技术

早期研究认为，抛罩运动为刚体的平动与转动，以及罩体的弹性变形，但弹性变形和刚体运动是不耦合的。因此，在阿里安－Ⅳ火箭和大力神－Ⅳ火箭整流罩分析［33－34］时，将刚体运动和弹性运动分别建模分析，最后进行叠加。

根据国内外研究经验，整流罩分离运动的研究可分为是否考虑气动力对整流罩分离运动的影响和是否考虑罩体弹性变形和刚体运动的偶合作用两个层面。在低空高速飞行器整流罩分离运动中，进行整流罩分离的动力学分析，按照多体动力学的方法［35］，既要考虑气动力对整流罩分离运动的影响，又要考虑弹性变形和刚体运动的耦合。

随着运载的需求，整流罩结构越来越向大型发展，而大型整流罩结构的柔性相对增加，在整流罩分离时极易发生扭转和弯曲等各种形式的振动，“呼吸运动”尤为明显;而且低空环境分离的要求更是给整流罩分离提供难题。因此，当前对整流罩分离动力学问题的研究，是为了解决整流罩分离过程的流固耦合和刚柔耦合问题，计算整流罩在特定工况下分离时的安全包罗区域和脱离后整流罩在气动力主导作用下运动轨迹。

当今，刚柔多体动力学和计算机辅助工程的发展使得抛罩类问题得以求解，仿真技术在整流罩分离运动中的应用很多，也解决了诸多工程问题。在解决整流罩刚柔耦合问题中，北京宇航工程研究所马忠辉［15］采用柔性动力学方法对整流罩分离进行分析，获得了分离运动参数;西北工业大学李哲等［36］采用ADAMS/Flex对大型整流罩结构进行有限元分析，并仿真获得分离过程中“呼吸运动”规律，给后续整流罩建模和研究提供了可用方法;上海交通大学的徐永成等［37］针对卫星整流罩建模分析，获得分离铰链构型和弹射筒等分离机构对分离运动的影响。在解决整流罩流固耦合问题中，北京航空航天大学张小伟等［38］采用流固耦合的动力学数值仿真方法，运用ANSYS和ADAMS联合求解柔性整流罩在气动力作用下的变形与轨迹，指出发展流固耦合动力学仿真的可行性。

3 低空高速整流罩分离技术研究思路及应用案例

总结国内外对低空高速整流罩分离研究现状，笔者根据工程实践与经验提出低空高速工况下大型整流罩分离技术的研究思路，旨在获取整流罩分离过程中整流罩在气动力、分离装置分离力和过载共同作用下壳体的分离运动过程、弹性变形及结构应力应变、分离过程中气动特性，为低空气动干扰下整流罩分离技术奠定基础，并依据此法对某型整流罩分离运动进行了仿真计算。

选取在稠密大气层内大型分瓣式整流罩为研究对象，考虑其气动力和弹性变形对整流罩分离运动的影响。采用CFD方法求解N－S方程得到分离过程气动力，多体系统动力学求解运动方程，并通过编程加载至动力学仿真模型;基于多体动力建模软件建立整流罩分离模型，最后使用CFD－6DOF方式计算整流罩运动轨迹。流场计算及动力学方程:

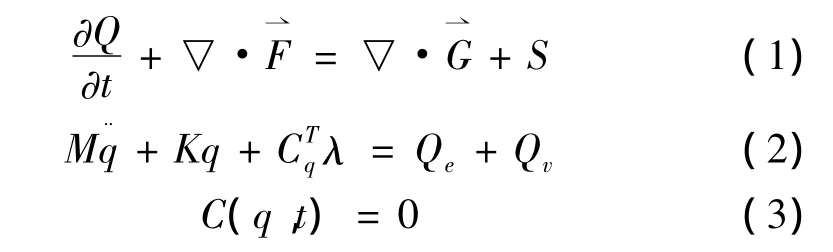
整流罩分离运动分析实施包含工况分析、数字样机建模和联合迭代仿真分析3部分，其分析流程见图2。

整流罩抛罩运动耦合计算流程:

(1)脱钩前，整流罩绕铰链定轴旋转运动，使用CFD计算固定张开角度下作用在整流罩面上的气动力;

(2)编写载荷转换程序，将气动结点力转化为有限元结点力，线性插值获得每个有限元结点气动载荷随张开角度的曲线，气动力转换如图3所示;

(3)依据整流罩刚柔耦合模型计算至整流罩脱钩时刻，如图4所示，外插至时间步长的下一位置点，选取时间步长数值积分，求得整流罩下一位置点的运动参数;

(4)将位置点坐标传递至CFD计算此时刻流场，继续向后插值，直至整流罩安全脱离。

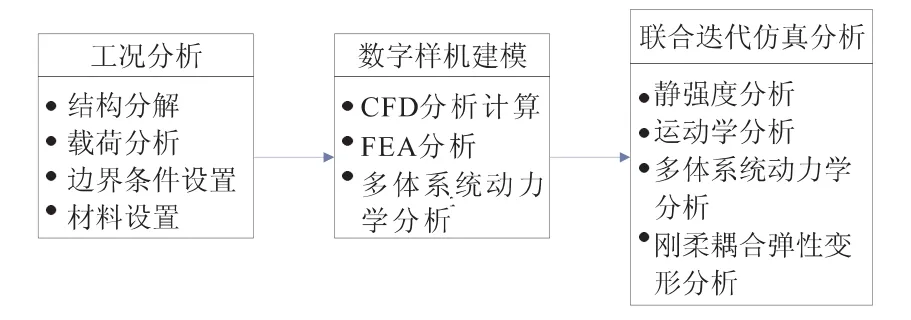
图2 整流罩分离运动分析流程Fig．2 Fairing separation analysis process

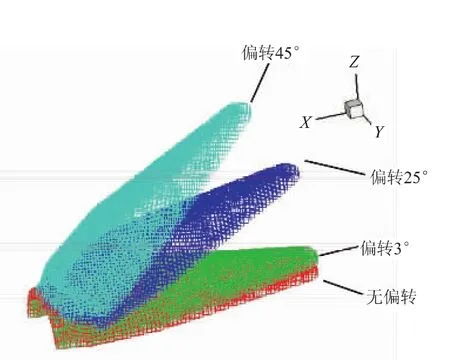
图3 气动力转换示意图Fig．3 View of fairing aerodynamic conversion

图4 刚柔耦合模型Fig．4 Rigid-flexible coupling model

在诸多工况中选取高度60 km、攻角5°工况，使用上述方法计算低空高速整流罩分离运动特性和变形特性，对比计算忽略气动情况下的分离角速度与考虑气动情况下的分离角速度如图5所示，下锥段危险点的变形量如图6所示。

由图5可知，低空(60 km高度)高速状态(考虑气动力)与现在通常的高空高速状态(不考虑气动力)相比，整流罩分离运动过顶时间由 0．353 s缩短到0．272 s，脱钩角速度由21．616 r/min 提高到48 r/min，气动力的影响很大。

由图6可知，整流罩下锥段主要变形为分离面的径向变形，“呼吸运动”明显，最大变形量达到72．6 mm，在整流罩与有效载荷间安全分离间隙较小的情况下，变形量会影响分离安全性。

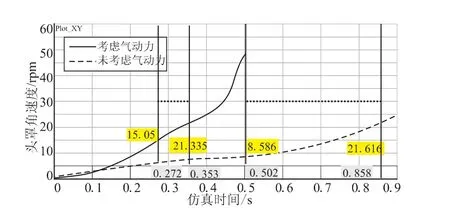
图5 整流罩角速度Fig．5 Fairing angular velocity

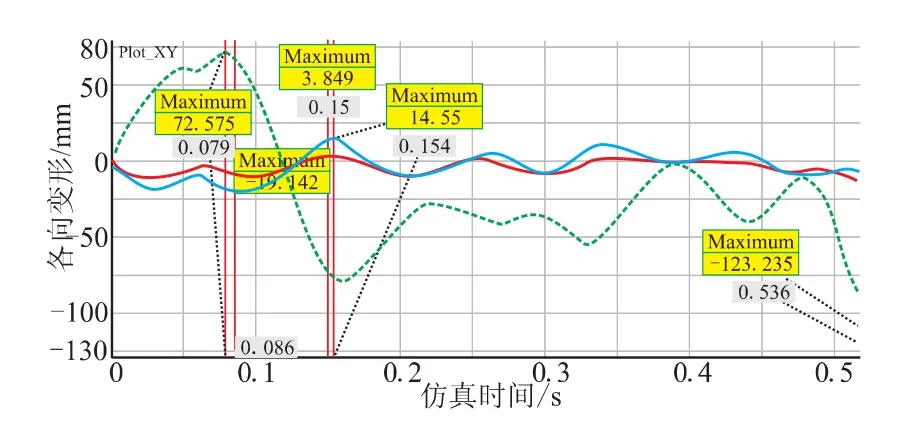
图6 整流罩危险点变形量Fig．6 Deformation of fairing＇s danger node

4 结束语

整流罩分离是典型的多体分离动力学问题，流场计算、刚体的大范围位移和结构变形相互耦合才能准确计算分离运动，较之高空整流罩分离，低空高速整流罩分离技术发展的较晚，经过飞行试验验证的很少，低空高速下的整流罩分离技术还需在以下方面进一步研究:

(1)复杂外形有效载荷与整流罩间的流场分析。整流罩分离运动中流场计算和有效载荷的形状尺寸有着很大关联，复杂外形的有效载荷会产生复杂的激波系，对整流罩的受力分布影响明显。

(2)流场、弹性变形与运动间的紧耦合分析技术。当前针对整个分离运动过程，为分离运动提出解决方法的不多。笔者在文中采用流场和位移场线性迭代的方法，可解决此类问题，但是计算量较大，自动程度不高，急需更紧密的耦合分析技术。

(3)准确的地面模拟验证技术。目前的风洞试验还难以验证低空高速下的整流罩分离运动，探索出合适的地面模拟技术，是提高低空高速整流罩分离技术的途径之一。

综上表明，低空高速飞行器整流罩分离技术还存在具有挑战性的问题亟需解决，只有把流体力学、多体动力学和弹性力学结合起来，并结合地面模拟验证技术，才能更好地解决低空高速整流罩分离问题。

［1］ 刘豪．2011年国外航天故障综述［J］．国际太空，2011(2):48－55．

［2］ 文清．美国“轨道碳观测卫星”发射失败［J］．国际太空，2009(4):32－33．

［3］ 唐伟，江定武，桂业伟，等．旋成体导弹头部母线线型的选择问题研究［J］．空气动力学学报，2010，28(2):218－221．

［4］ 赵晓慧．巡航导弹锥形头罩分离仿真分析［D］．长沙:国防科学科技大学，2009．

［5］ 逄华．日本H－2火箭卫星整流罩分离与抛罩试验［J］．世界导弹与航天，1991(6):29－33．

［6］ Cheng S C．Payload fairing separation dynamics［C］//The 35th AIAA(American Institute of Aeronautics and Astronautics)/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference pt．4，1994．

［7］ 汪顺亮，董文源．长征四号卫星整流罩分离动力学研究［J］．中国航天，1993(8):36－38．

［8］ 周镜昆．ZN－3探空火箭头罩分离的分歧及弹射分离器的设计［J］．宇航学报，1994，15(3):1－10．

［9］ 雷勇军，卓曙君，郑荣跃，等．卫星整流罩结构动力特性与分离运动分析［J］．国防科技大学学报，1997，19(4):23－27．

［10］ 赵丽琴．整流罩模拟假弹头空间运动学与动力学分析［D］．西安:西安电子科技大学，2006．

［11］ 李长纯．长征二号E火箭有效载荷整流罩分离技术［J］．中国航天，1992(9):11－15．

［12］ 王志刚，李伟．一种新型弹体结构的导弹分离动力学建模与仿真［J］．科学技术与工程，2010，10(14):3403－3407．

［13］ 范庆志，孙秦．飞行器头罩分离技术及设计方案分析研究［J］．机械设计与制造，2008(9):8－10．

［14］ 李大耀．中国探空火箭40年［M］．北京:宇航出版社，1998:65－70．

［15］ 马忠辉．大型弹性整流罩分离特点分析［J］．中国科学E辑，2009，39(3):482－489．

［16］ 纪学，孙秦，高扬．大型薄壁壳体结构动力学响应特性的数值模拟［J］．机械强度，2011，33(5):782－785．

［17］ 刘君，王巍，郭正，等．稠密大气层内火箭头罩动态分离过程数值模拟［J］．弹道学报，2006，18(3):34－38．

［18］ Baum J D，Luo Hong，LÊhner R．Application of unstructured adaptive moving body methodology to the simulation of fuel tank separation from an F－16C/D fighter［R］．AIAA 9720166．

［19］ 杨爱明，乔志德．基于运动嵌套网格的前飞旋翼绕流N－S方程数值计算［J］．航空学报，2001，22(5):434－436．

［20］ 刘鑫，陆林生．重叠网格预处理技术研究［J］．计算机工程与应用，2006，42(1):23－26．

［21］ 唐志同，李彬，郑鸣，等．飞行器外挂投放数值模拟［J］．空气动力学学报，2009，27(5):592－596．

［22］ 张玉东，纪楚群．子母弹分离过程的数值模拟方法［J］．空气动力学学报，2003，21(1):47－52．

［23］ 招启军，徐国华．计入桨叶运动的旋翼CFD网格设计技术［J］．南京航空航天大学学报，2004，36(3):288－293．

［24］ 田书玲，伍贻兆，夏健．用动态非结构重叠网格法模拟三维多体相对运动绕流［J］．航空学报，2007，28(1):46－51．

［25］ 张来平，张涵信，高树椿．矩形/非结构混合网格技术及在二维/三维复杂无粘流场数值模拟中的应用［J］．空气动力学学报，1998，16(1):79－88．

［26］ Seungsoo Lee，Minwoo Park，Kum Won Cho，Jang Hyuk Kwon．A new automated chimera method for the prediction of store trajectory［R］．AlAA 99－3131．

［27］ Zhang S J，Zhao X．Computational studies of stage separation with an unstructured chimera grid method［R］．AIAA 2007－5409．

［28］ Zhang S J，Liu J，Chen Y S，Zhao X．Numerical simulation of stage separation with an unstructured chimera grid method［R］．AIAA 2004－4723．

［29］ 郭正．包含运动边界的多体非定常流场数值模拟方法研究［D］．长沙:国防科技大学，2002．

［30］ Anandhanarayanan K，Konark Arora，Vaibhav Shah，et al．Separation dynamic of air－to－air missile using a grid－free euler solver［J］．2013，50(3):725－731．

［31］ 张永杰，孙秦．整体式头罩分离运动轨迹可靠性分析［J］．箭弹与制导学报，2011，31(1):19－22．

［32］ Melike Nikbay，Muhammet N Kuru．Reliability based multidisciplinary optimization of aeroelastic systems with structural and aerodynamic uncertainties［J］．Journal of Aircraft，2013，50(3):708－715．

［33］ Villalaz P A．阿里安4卫星整流罩的分离特性预示［J］．国外导弹与航天运载器，1989(2):22－29．

［34］ Cheng S C．Payload fairing separation dynamics［R］．AIAA 94－1543－CP．

［35］ 洪嘉振．计算多体系统动力学［M］．北京:高等教育出版社，1997．

［36］ 李哲．大型整流罩分离动力学简化建模及仿真分析［J］．固体火箭技术，2012，35(5):583－587．

［37］ 徐永成，苟永杰，王石刚．某卫星整流罩分离仿真分析［J］．上海航天，2009，26(1):53－56．

［38］ 张小伟，王延荣，谢胜百，等．弹性整流罩分离的流固耦合仿真方法［J］．北京航空航天大学学报，2009，35(8):976－979．