相容滤子完备偏序集上投射算子的几个性质
朱润秋,卢 涛
(淮北师范大学 数学科学学院,安徽 淮北 235000)
0 引言
连续格理论集序结构、代数结构、拓扑结构的研究于一体,是拓扑学和理论计算机科学研究者共同关注的一个重要领域[1-3].随着研究的深入,人们将连续格中关键的双小于关系移植到偏序集上,产生了连续偏序集的概念,得到了丰富的成果[4-8].
近年来,徐罗山教授针对实数集、自然数集的序结构特点(不是定向完备的)在文献[9-11]中提出了相容定向集、相容定向完备偏序集的概念,将实数集和自然数集引入到研究对象中来,推广了Domain理论的研究范围,得到了许多好的结果.本文对偶地引入了相容滤子集、相容滤子完备偏序集的概念,并研究了偏序集及相容滤子完备偏序集上投射算子的几个性质,得到的相应结果丰富了偏序集上的算子理论.
1 预备知识
先介绍一些预备知识.
定义1[4]设L是一个偏序集,L的非空子集A称为滤子的,若对任意的a,b∈A,存在c∈A,使得c≤a,c≤b.若L中的每一个滤子集都有下确界,则称L是滤子完备偏序集.
定义2设L是一个偏序集,Ø≠F⊆L,若F是滤子且存在d∈L使得F⊆↑d,则称F为L的相容滤子集.
定义3设L是一个偏序集,若对L中每一个相容滤子集F,F在L中的下确界infF存在,则称L是相容滤子完备偏序集.
定义4[4]设L是一个偏序集,
(1) 若p:L→L是单调的,幂等的(即p=p∘p),则p称为投射算子(简称投射).
(2) 若c是L上的投射算子且lL≤c,则称c为闭包算子.
(3) 若k是L上的投射算子且k≤lL,则称k为核算子.
注:以下我们记p(L)是L在p下的像(关于L的诱导序),注意到p:L→L是幂等的,则对任意的x∈p(L),我们有p(x)=x.
2 主要结果
命题1设L是相容滤子完备偏序集,p:L→L是投射算子,则
(2) 若p是核算子,则p(x)=max{y∈p(L)|y≤x},∀x∈L;
(3) 若p是Scott连续的,则p(L)为相容滤子完备偏序集.
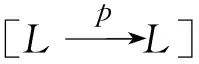



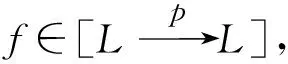
(2) 若p是核算子,则∀x∈L,p(x)≤x,p(x)∈p(L),即
p(x)∈{y∈p(L)|y≤x}
又∀y∈{y∈p(L)|y≤x},有y=p(y)≤p(x),故
p(x)=max{y∈p(L)|y≤x},∀x∈L.
(3) 设F⊆p(L)是相容滤子集,由L是相容滤子完备偏序集,故下确界infF在L中存在,又p:L→L是Scott连续的投射算子,则p(infF)=infp(F)=infF,即infF∈p(L),故p(L)为相容滤子完备偏序集.
引理1设g:L→M是完备格间的保交映射,则g(L)在M中关于交封闭.
证明:令Y⊆g(L)且X=g-1(Y),则g(X)=Y.由g保交知
infY=infg(X)=g(infX)
因此infY∈g(L),即g(L)在M中关于交封闭.
注:上述结论对于g保滤子交时不成立,即若g:L→M是完备格间的保滤子交映射,则g(L)在M中不一定关于滤子交封闭.但当映射为投射时,我们有下面的结论成立.
命题2设P:L→L是偏序集L上的投射算子,p(L)是L在p下的像,若X⊆p(L)且infLX存在,则infp(L)X存在且infp(L)X=p(infLX).
证明:设X⊆p(L)且infLX存在,∀x∈X,由infLX≤x以及p是单调的,有p(infLX)≤p(x),又p是幂等的,则p(infLX)≤p(x)=x,从而p(infLX)是X在p(L)中的一个下界.令a∈p(L)是X在p(L)中的另一个下界,则a≤infLX,因此由p是单调的、幂等的知a=p(a)≤p(infLX),故p(infLX)是X在p(L)中的最小的下界,即infp(L)X存在且infp(L)X=p(infLX).
命题3设p:L→L是偏序集L上的投射算子,p(L)是L在p下的像,若p保滤子交,则p(L)在L中对滤子交封闭,即对每一个滤子集F⊆p(L)且infLF存在,则infp(L)F存在且infp(L)F=infLF.
证明:设F⊆p(L)是滤子集且infLF存在,则由命题1知,infp(L)F存在且infp(L)F=p(infLF),若p保滤子交,则p(infLF)=infLp(F),又p是幂等的,则有infLp(F)=infLF,从而infp(L)F=infLF.
命题4设p:L→L是偏序集L上的投射算子,若p保相容滤子交,则p(L)在L中对相容滤子交封闭,即对每一个相容滤子集F⊆p(L)且infLF存在,则infp(L)F存在且infp(L)F=infLF.
证明:设F⊆p(L)是相容滤子集且infLF存在,则由命题1知infp(L)F=p(infLF),若p保相容滤子交,则p(infLF)=infLp(F),又p是幂等的,则有infLp(F)=infLF,从而infp(L)F=infLF.
注:若L为相容滤子完备偏序集,p:L→L是保相容滤子交的投射算子,则命题3,命题4可简述为:infp(L)F=p(infLF)=infLF,其中F⊆p(L)为相容滤子集.
[1]Gierz G. A Compendium of Continuous Lattices [M]. Berlin: Springer-Verlag,1980.
[2]Engelking R.General topology[M]. Warszawa:Polish Sic Publ,1977.
[3]郑崇友,樊 磊,崔宏斌.Frame与连续格[M]. 北京:首都师范大出版社,2000.
[4]Gierz G, Hofmann K H, Keimel K, etal. Continuous Lattice and Domains [M].Cambridge: Cambridge University Press, 2003.
[5]邓自克. 广义连续格I,II [J]. 湖南大学学报(自然科学版), 1996,23(3): 1-3; 1996,23(5):1~3.
[6]何卫民. 相容连续Domain的遗传性[J]. 模糊系统与数学, 2010,24(1): 56~59.
[7]肖 璨,姜广浩,杨 慧. 偏序集上的理想极大滤子及其应用[J]. 吉林师范大学学报(自然科学版), 2013,34(1):13~15.
[8]刘德金. 关于子基的正规空间和相对正规性[J]. 吉林师范大学学报(自然科学版), 2013,34(4): 87~89.
[9]徐罗山. 区间数系的内蕴拓扑及度量表示[J]. 扬州大学学报(自然科学版), 1999,2(1):1~5.
[10]徐罗山. 相容连续偏序集及其定向完备化[J]. 扬州大学学报(自然科学版), 2000,3(1): 1~10.
[11]徐罗山. 相容L-domain及其相关范畴性质[J]. 扬州大学学报(自然科学版), 2002,5(1): 1~7.

