遗传算法求解约束优化问题时产生初始种群的改进方法

徐 梅，文士发，王福林，官 林

（东北农业大学工程学院，哈尔滨 150030）

遗传算法求解约束优化问题时产生初始种群的改进方法

徐 梅，文士发，王福林，官 林

（东北农业大学工程学院，哈尔滨 150030）

研究提出初始内点产生新方法，该方法根据约束优化问题的特点，构造由约束条件构成目标函数，将求初始内点问题转化为求解一系列无约束优化问题，通过求解这些无约束优化问题，实现初始内点求解；研究初始种群其余个体产生的一种方法。结果表明，初始种群产生关键在于求得一个初始内点，求得初始内点后，其他个体的产生将占据较少时间。试验验证文章给出的初始种群产生方法快速可靠，可以克服有些约束优化问题初始种群难以产生问题。

遗传算法；初始内点；初始种群；约束优化问题

遗传算法（Genetic algorithms，GA），是由美国密歇根大学Holland创立[1]，思想基础来源于群体遗传学和生物进化论，是基于基因遗传学和自然选择原理的一种群本寻优算法。特别适用于传统搜索方法难以解决的复杂非线性约束优化问题，被广泛用于机器学习、组合优化、系统工程、自适应控制、人工智能、规划设计、智能制造系统、智能机器系统、人工生命等领域[2-4]。与其他寻优算法相比，遗传算法具有以下特点：①遗传算法是群体寻优算法，搜索从许多点开始，可防止搜索过程收敛于局部最优解，提高求得全局最优解的可能性；②遗传算法通过适应度函数实现优秀种群选择，避免其他推导和附属信息，求解具有较好的鲁棒性；③对寻优函数无限制，既不要求函数连续，也不要求函数可微；可以是显函数，也可以是隐函数（映射矩阵、神经网络），因而应用广泛；④遗传算法是一种启发式搜索法，既不是穷举法，也不是完全随机搜索，只要基因位置选择恰当，遗传操作合理，搜索效率往往较高，仅需有限次计算，便可得到理想最优解；⑤具有并行计算优点，可用大规模并行计算大幅提高运算速度；⑥特别适用于复杂大系统的优化求解。

遗传算法虽然具有诸多优点，但在用于求解约束优化问题时，用产生随机数方法得到足够数量初始种群，有时相当困难，需要几十个小时甚至更长时间才能产生。本文对此问题进行研究，提出初始种群产生的一种新方法。

1 用遗传算法求解约束优化问题的方法概述

约束优化问题是一类广泛存在于科学研究和工程应用中的优化问题，一般约束优化问题可描述为：

式中，X=(x1,x2,…,xn)T是n维欧式空间En中的点(向量)，目标函数f(X)和约束条件gj(X)，hk(X)均为X的实函数[5]。

求解约束优化问题主要的挑战是如何有效平衡约束优化可行解区域和不可行解区域之间的搜索，即设计一个有效的约束处理方法定位全局最佳的可行区域。针对处理不可行解这一问题，在最近几十年的进化算法研究中，许多新思路被提出，如修复、惩罚函数等。其中修复是将不满足约束条件的解进行修复，使其成为满足约束条件的解。

将遗传算法应用于求解约束优化问题时，需运用变量替换等方法把等式约束替换，采用遗传算法求解约束优化问题的数学模型可表示为：

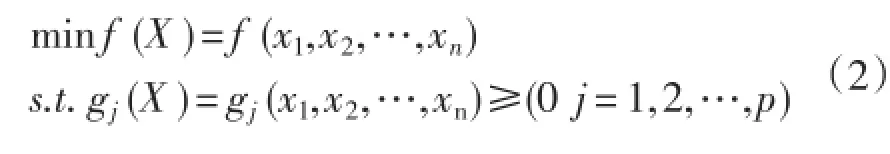
目前，遗传算法处理约束优化问题时，一般采用惩罚函数法、解码器法、算子修正法和可行解搜索法[6]。惩罚函数法是约束优化问题中比较常用的方法，通过在适应值函数上添加一个惩罚项，将原问题变成一个无约束性质问题。惩罚函数法简单易行，但在实际操作中，惩罚因子较难。解码器法不同于惩罚函数法，是通过特殊编码方式避免产生不可行个体，此方法效率较高，并非所有约束问题都能使用这种方法进行求解。算子修正法通过设计专门的算子，以保证可行个体产生的个体仍是可行个体，这些遗传算子对可行解空间封闭，算子修正法只能用于线性约束问题，而不能用于非线性约束问题。可行解搜索法对算子修正法进一步改进，适用于线性和非线性的约束优化问题。

在求解约束优化问题时，遗传算法起始于一组随机选择的初始个体，对其进行进化操作，包括选择、交叉、变异等。该算法的进行主要依赖目标函数（适应度函数），优秀个体将具有较高适应度函数值，较差的个体将具有较低适应度函数值。求解过程中需要评价的目标函数和约束条件，而不需要其他更复杂信息。遗传算法具有随机性特点，使其能避免陷入局部最优的优势。遗传算法第一步是产生一组可行的解，将其作为初始种群。算法收敛速度、算法的性能受初始种群影响极大，因此初始种群确定尤为重要。

2 初始内点的一种新求法

定义1：对于种群中的任意一个个体，若该个体满足（2）式中的所有条件，则该个体称为可行个体，若该个体不满足所有约束条件，则该个体为非可行个体；

定义2：最初可行个体的全体称为初始种群，初始种群中个体的数量称为种群规模；

定义3：对于种群中的任意一个个体，若该个体满足（3）式中的所有条件，则该个体称为内点。

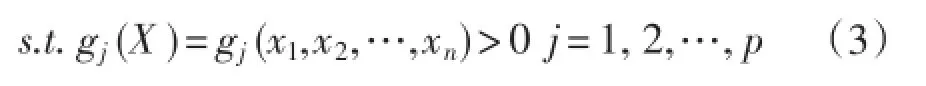
初始种群方法是在内点基础上，采用对内修正方法实现。初始种群的产生可分为两种情况。第一种情况是可人为给出1个初始内点；第2种情况是无法人为给出1个初始内点。针对第2种情况，只要运用合适的搜索方法，产生出1个内点，则等同于第1种情况。因此整个过程的关键是初始内点产生，具体步骤如下。先任取一点，如果其以严格不等式满足所有约束，则就是要求初始内点。若该点以严格不等式满足一部分约束，而不能以严格不等式满足另外约束，则以不能严格满足的这些约束函数为假拟目标函数，而以严格满足那些约束函数形成障碍项，构造1个无约束性质的函数。求出上述函数在点的单位负梯度向量，在此方向上进行搜索，得出函数值小于点的新点若仍不为内点，就如上述方法，减小障碍因子，构造出新的目标函数继续进行搜索，直至求出的点严格满足所有约束，成为初始内点为止。

求初始内点的迭代步骤如下：

②确定指标集Tk和Tˉk

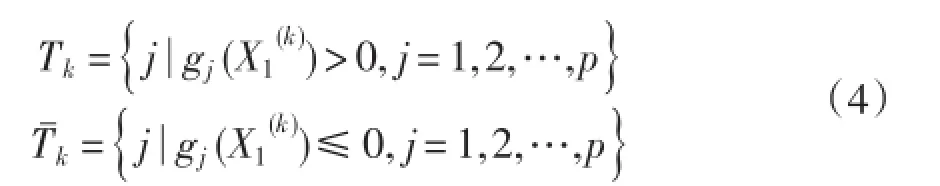
③检查Tˉk是否为空集，若为空集，则取X(k)为初始内点，迭代停止；否则，转下步。

④构造如下目标函数

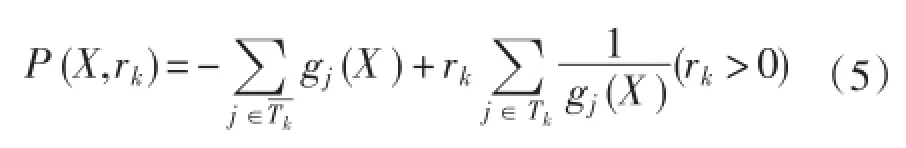
⑤求函数P(X,rk)在)处的单位负梯度方向

式中，λk为搜索步长。

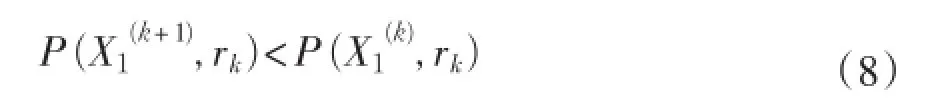
按上述步骤求得的点就是要求的初始内点。

3 初始种群其余个体的产生方法

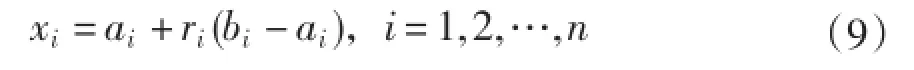
式中，ai是变量xi的下限，bi是变量xi的上限，ri为0～1的随机数。

若X2满足（10）式

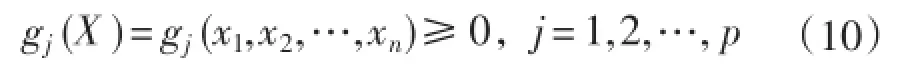
则产生下一个个体X3，若不满足，则

式中，α为收缩系数（0≤α＜1）。

当α取值为0.5时，实际上就是取X1与X2的中点，如图1所示。

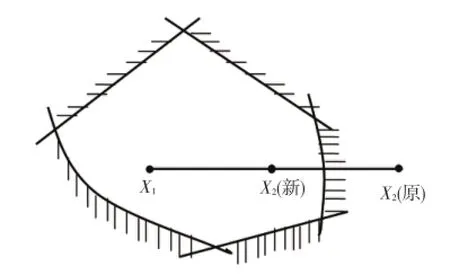
图1 X1与原X2和新X2之间的关系Fig.1 Relationship of X1,primary X2and new X2

若按（11）式收缩1次，X2还不是可行个体，则按（12）式将α减半，

再按（11）式继续向X1收缩靠拢，直至使X2成为可行个体为止。

X2产生以后，再产生个体X3，采用与X2同样处理方法，可使X3成为可行个体。仿照同样方法，直至产生所有可行个体为止。

4 示例计算

为评价本文提出的初始种群产生方法的性能，选取两个相当复杂的测试函数进行测试。电脑配置为i5内核、1 GB内存，以Matlab 7.1为编程平台。用产生所有满足约束条件的初始种群耗时多少作为评价标准，将本文提出方法的测试结果与常用随机产生方法的测试结果进行对比，测试函数及结果见下文。

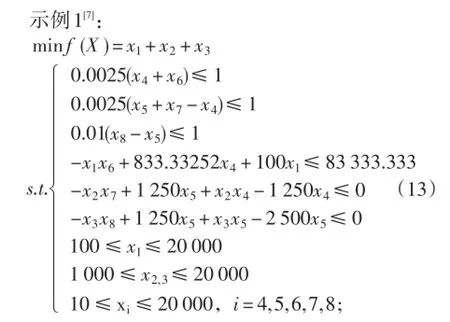
在示例1中，变量x1～x8的上下限在模型中已经给定，按照随机产生的方法和本文提供的方法，在不同种群规模下，分别统计100次运行的结果。当产生满足要求的初始种群时，随机产生方法和本文提供的方法所用时间的平均值见表1。

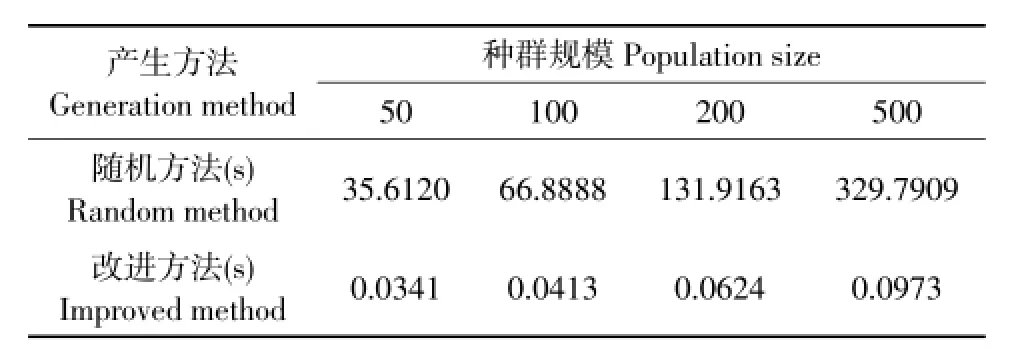
表1 示例1中不同种群规模下初始种群产生时间比较Table 1 Comparison of creation time in different size of population in example 1

在示例2中，变量x1～x12下限为0，x10,x11,x12取值上限已确定。x1～x9取值上限定为800，按随机产生方法和本文提供方法，在不同种群规模下，分别统计100次运行结果（由于随机方式比较慢，只统计5次）。当产生满足要求的初始种群时，随机产生方法和本文提供的方法所用时间平均值见表2。

表2 示例2中不同种群规模下初始种群产生时间比较Table 2 Comparison of creation time in different size of population in example 2

从表1和2可以看出，本文给出的方法能够加快初始种群的产生速度，并且随着种群规模的增大，优势更加明显。从示例2可以看出，对于约束比较复杂的问题，用随机的方法产生初始种群需要几小时、十几小时甚至更长时间，严重影响遗传算法效率，而采用本文方法则可提高遗传算法求解复杂约束优化问题效率。

5 讨论与结论

约束优化问题是工程领域最常见问题，由于问题复杂性，至今尚无确定性搜索算法求解。遗传算法已成功求解约束优化问题。Bean等提出基于罚函数求解方法[9]，Man等提出基于修改算子求解方法[10]，刘大莲等提出内外交叉遗传算法[11]，何家莉等用遗传算法解决含有等式约束优化问题[12]。遗传算法在求解约束优化问题时，关键是初始种群产生，为能在可行域内产生初始种群，传统遗传算法采用随机加筛选产生方法，使初始种群产生速度被限制，降低算法性能。王福林等提出随机加修复产生方法[8]，使初始种群产生速度得到提高。但在求解约束条件较苛刻优化问题时，由于该方法第1个可行域内点仍是采用随机方式产生，导致初始种群产生时间偏长。本文针对这一缺陷，提出改进方法，将基于罚函数梯度下降法应用到初始种群产生中，以约束条件构造目标函数为搜索对象，寻找第1个可行域内点，保证第1个初始可行域内点快速产生，加快初始种群产生速度，提高遗传算法求解复杂约束优化问题效率。

[1]Holland J H.Adaptation in natural and artificial systems[M].USA: The University of Michigan Press,1975.

[2]朱剑英.智能系统非经典数学方法[M].武汉:华中科技大学出版社,2001.

[3] 邵克勇,李鑫,邱跃峰,等.模仿二倍体繁殖的改进遗传算法[J].系统仿真学报,2012,24(4):816-820.

[4]李菲,王福林,吴昌友.基于遗传神经网络的农村用电量需求预测[J].东北农业大学学报,2009,40(2):106-110.

[5]胡运权,郭耀煌.运筹学教程[M].北京:清华大学出版社, 2007:152-153.

[6]余文,李文厚.遗传算法对约束优化问题的研究综述[J].计算机科学,2002(6):98-101.

[7]纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009:105.

[8]王福林,吴昌友,杨辉.用遗传算法求解约束优化问题时初始种群产生方法的探讨[J].东北农业大学学报,2004,35(5): 608-611.

[9]Bean J C,Hadj-Alouane A.A dual genetic algorithm for bound⁃ed integer programs[J].Ann Arbor,1992,1001:48109-2117.

[10]Man K F,Tang K S,Kwong S.Genetie algorithms:Concepts and designs aves disquette[M].New York:Springer,1999.

[11]刘大莲,徐尚文.求解约束优化问题的内外交叉遗传算法[J].系统工程理论与实践,2012,32(1):190-195.

[12]何家莉,宣士斌.含有等式约束优化问题的遗传算法[J].计算机工程与设计,2008,29(5):1253-1255.

Improved method on generation of initial population by using GA for solving constrained optimization problems

XU Mei,WEN Shifa,WANG Fulin, GUAN Lin(School of Engineering,NortheastAgricultural University,Harbin 150030,China)

Through the research we present a new method about initial interior point's generation, firstly constructed a constraint posed by the objective function,which is based on the characteristics of constrained optimization problems,and translate the problem of evaluating the initial interior point into solving the problem of solving a series of unconstrained optimization,by solving the unconstrained optimization problem,we achieve the solution of the initial interior point;Based on this,the research has given a method on the generation of the rest initial population individuals.The results showed that the key to generate the initial population was to obtain an initial point,the production of other individuals would take less time after the initial internal point was obtained.We verified by examples that the initial population generation method given by the paper was a fast and reliable method,and thus overcame the problem,which initial population was difficult to be produced in some constrained optimization problems.

genetic algorithms;initial interior point;initial population;constrained optimization problem

TP301.6

A

1005-9369（2014）07-0104-04

时间2014-7-4 17:18:39 [URL]http://www.cnki.net/kcms/detail/23.1391.S.20140707.0843.008.html

徐梅,文士发,王福林,等.遗传算法求解约束优化问题时产生初始种群的改进方法[J].东北农业大学学报,2014,45(7):104-107.

Xu Mei,Wen Shifa,Wang Fulin,et al.Improved method on generation of initial population by using GA for solving constrained optimization problems[J].Journal of Northeast Agricultural University,2014,45(7):104-107.(in Chinese with English abstract)

2013-09-27

国家自然科学基金项目（31071331，1151z004）

徐梅（1957-），女，教授，硕士，博士生导师，研究方向为农业系统工程。E-mail:xumei2009@163.com