基于分形技术的阶跃阻抗带通滤波器

马 亮，王海彬

（机电动态控制重点实验室，陕西 西安710065）

0 引言

由于普通滤波器寄生通带一般出现在主通带的二倍或三倍的地方，因此不利于抑制高次谐波的输出。前人利用阶跃阻抗［1］谐振器（简称SIR）构成微波带通滤波器，通过调节耦合段微带线与过渡段微带线的阻抗比，可以使得寄生通带远离主通带整数倍频率点［2］，从而为解决谐波抑制问题提供了有效途径。然而，由于SIR滤波器要求耦合段与过渡段特性阻抗有阶跃性变化，微带线宽随之发生突变导致电流出现不连续性［3］，因此经典分析方法设计的SIR滤波器在实际应用中会出现较大的设计偏差，使滤波器的电特性及寄生通带与设计预期不相吻合。针对上述问题，引入分形思想，通过改变阶跃阻抗谐振器形状的方法，设计基于分形技术的SIR 带通滤波器。

1 SIR 滤波器结构

SIR 是由两个以上具有不同特征阻抗的传输线组合而成的横向电磁场或准横向电磁场模式的谐振器［4］，如图1 所示。

图1 SIR 结构Fig.1 SIR structure

图1中传输线的特征阻抗和等效电学长度分别为Z1，Z2和θ1，θ2。阻抗比K=Z2／Z1是SIR最重要的参数。

SIR 滤波器由多个SIR 级联构成，根据实际需要可以有不同的耦合方式。本文主要针对平行耦合SIR滤波器进行研究。n阶结构SIR平行耦合微带滤波器由n个SIR 级联组成［5］如图2所示。

图2 SIR 滤波器Fig.2 SIR Filter

利用LINECALE计算微带线以及缝隙的尺寸，计算得出：单支微带线宽W =0.64 mm，线长L=7.96mm，耦合微带线计算尺寸如表1所示，表中W、S、L分别代表各耦合微带线的线宽、缝隙宽度和线长。

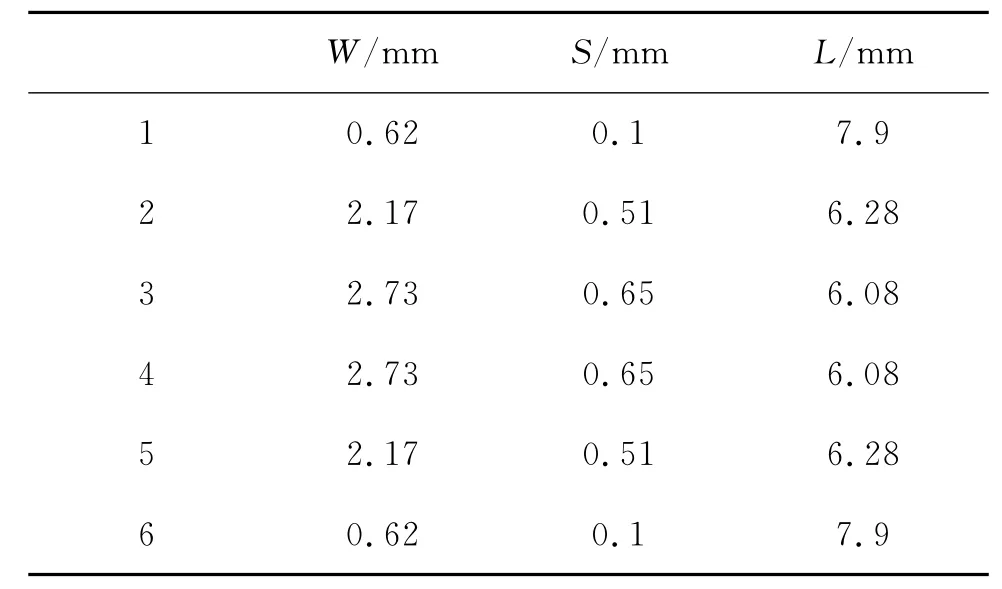
表1 耦合微带线尺寸Tab.1 Size of the coupled microstrip

2 分形SIR 带通滤波器设计

2.1 SIR 滤波器设计

根据实际应用，下面设计一个中心频率3GHz，带宽0.4GHz SIR平行耦合带通滤波器，相对带宽：ω=0.13，通带纹波：R=0.1dB，通带内反射系数S（1，1）≤-20dB，传输系数S（2，1）≥-3dB，滤波器基板采用介电常数为2.2，厚度为1 mm 的介质板。采用5阶契比雪夫低通滤波器原型，查表得出低通原型滤波器元件值为：g1=g5=1.146 8，g2=g4=1.371 2，g3=1.975 0，g6=1。

根据文献［6］，SIR 滤波器寄生通带中心频率θS与通带中心频率θ之比的关系如公式（1）所示：

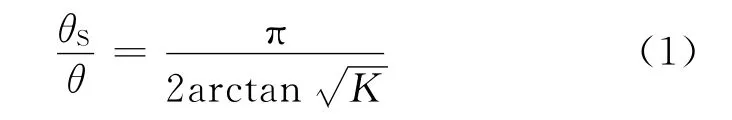
根据公式（1）分析得知，当K=1时，θs／θ=2，寄生通带将出现在2倍主通带频率点处；当K ＞1时，θs／θ＜2，且随着K 值的增大，滤波器寄生通带的位置将向主通带靠近；当K ＜1时，θs／θ＞2，且随着K 值的减小，滤波器寄生通带的位置将远离主通带，据此，为了更好地进行谐波抑制，应尽可能选取更小的K 值，但是，随着K 值的逐渐减小，SIR 滤波器耦合段与过渡段微带线宽度突变也将越来越明显，由此带来的电流不连续性也将越来越强烈，因此K 值的选取也不应过小［7］。通过以上分析，结合实际需要，本文选取K=0.5，通过计算得知滤波器寄生通带理论上应该出现在7.7GHz处。

最后，将以上微带线尺寸带入SIR 滤波器结构，构成SIR 带通滤波器。然而，由于上述设计方法并没有考虑微带线宽发生突变导致的电流不连续性，会造成实际设计结果有较大的设计偏差，因此，需要对SIR 滤波器进行分形优化。

2.2 利用KOCH 分形技术优化滤波器

1975年，法国人B.B.Mandelbort第一次提出了分形的概念。一般来说，具有分形结构的物体都具有空间填充性和自相似的特性。经典的Koch分形由荷兰数学家Helge Von Koch 首次提出并命名，Koch分形是增加Koch曲线的迭代次数使其结构形状逐渐变为岛屿形状，又可称为Koch 岛。由于Koch 岛分形结构［8］成阶梯锯齿状分布，对于传输信号而言，其不连续性将大大减缓［9］，而对于截止信号，这种宽度的渐变对截止状态不产生影响，因此广泛应用于抑制高次谐波的设计中。

本文就利用Koch分形技术对SIR 滤波器进行分形。Koch曲线的生成方法是把一条直线分成三段，将中间的一段用具有一定夹角的两条等长的折线代替，形成一个生成元，然后再把每个直线段用生成元进行代换［10］，经n 次迭代就得到n 阶KOCH曲线，但迭代次数如果太多，增加了复杂度，因此，从实际制作考虑，曲线的迭代次数不宜太大。图3为一阶KOCH 分形示意图。图4为KOCH 分形后的SIR 示意图。一般来说，对滤波器进行分形优化需要对KOCH 生成元的尺寸以及迭代次数进行多次调整，反复试验，最终才能达到优化目标。

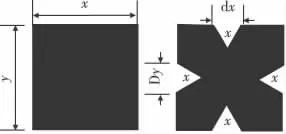
图3 一阶KOCH 分形示意图Fig.3 Dranving of the first-order KOCH fractal techlogy

图4 分形SIR 示意图Fig.4 Dranving of fractal SIR

3 仿真验证与结果分析

利用表1的数据通过电磁仿真软件ADS，建立SIR 滤波器原理图仿真模型，仿真结果如图5、图6所示。从图5可以看出，滤波器通带内S（1，1）≤-20dB，S（2，1）≥-3dB，所设计的滤波器原理上满足设计要求；从图6可以看出，滤波器第一寄生通带出现在7.6～7.8GHz处，与之前理论推算一致。

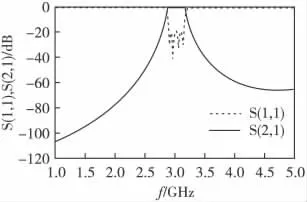
图5 通带频率响应结果Fig.5 Passband frequency response

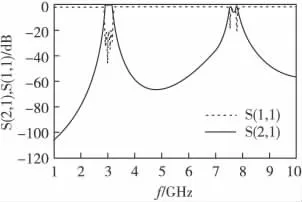
图6 宽频带频率响应Fig.6 Wideband frequency response

由于ADS在原理图仿真过程中，其内部算法仅仅是利用微带线经验公式进行建模分析，而没有分析微带线上电磁场的分布，从而忽略了耦合段与过渡段特性阻抗阶跃性变化带来的微带线宽发生突变而导致的电流不连续性问题，因此会造成实际设计的产品与仿真结果不符。而三维仿真软件HFSS是一款场级仿真软件，可以真实地描述微带线上的电磁场分布，仿真结果更接近实际。因此需要利用三维仿真软件HFSS进行仿真，利用表1中计算得出的数据建立的仿真模型如图7。

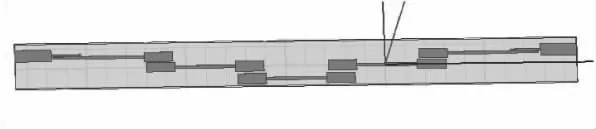
图7 SIR 带通滤波器的HFSS仿真模型Fig.7 HFSS simulation model of the SIR bandpass filter

通过对图7中模型的仿真，得到的仿真结果如图8。

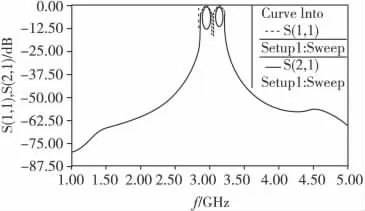
图8 SIR 滤波器HFSS仿真结果Fig.8 The simulation result of SIR Filter in HFSS

由图8可以看出，所设计的滤波器通过HFSS仿真的结果与图6有很大差异，通带内S（1，1）≥-15 dB，S（2，1）≤-12.5dB，与设计指标产生了较大的偏差，这种现象是由于SIR耦合段与过渡段宽度相差太大造成电流的不连续性过于显著而产生的，因此，需要对滤波器进行分形优化，首先对滤波器微带进行一定程度的微调，减小中间4对耦合微带线（即w2—w5）的宽度，增大单支微带线的以及靠近端口两对耦合微带线的宽度（w1，w6），同时增加最靠近端口两对耦合微带线之间缝隙（s1，s6）的宽度，通过反复优化，最终采用长0.3x、宽0.3y（如图3 所示）的比例进行KOCH 一次迭代分形。分形优化后的滤波器仿真模型如图9所示，仿真结果如图10所示。

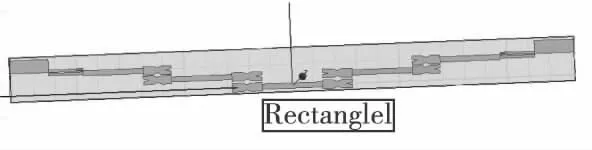
图9 分形SIR 滤波器HFSS仿真模型Fig.9 HFSS simulation model of the fractal SIR filter

从图10中可以看出，不仅通带内S（1，1）≤-20dB，S（2，1）≥-3dB，而且分形后SIR 带通滤波器的寄生通带中心频率控制在7.8GHz附近，通带与寄生通带位置与图6基本吻合，并没有因为在优化过程中发生很大改变，满足设计要求。

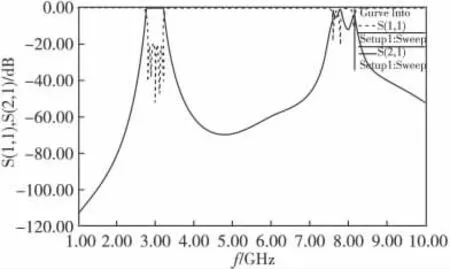
图10 分形SIR 滤波器宽频响应Fig.10 Wideband frequency rosponse of the fractal SIR filter

4 结论

本文提出了基于分形技术的阶跃阻抗带通滤波器，该滤波器可以很好地解决电流不连续性带来的设计偏差问题。仿真结果表明该滤波器不仅在通带内保持良好的性能，而且寄生通带位置与预期设计目标相符，保证了对谐波的抑制。同时，为了减少电流不连续性带来的影响，在分形优化前对滤波器微带进行了一定程度的微调，使得滤波器加工难度有所降低。因此，将分形技术应用到SIR 带通滤波器设计中，为设计有谐波抑制功能的滤波器提供了一种新的思路。然而，目前只是对分形技术SIR 带通滤波器进行设计仿真，在实际的制作应用方面还有待进一步的验证。

［1］林杞楠，张雅绮.非等长微带SIR 平行耦合带通滤波器的设计［J］.微波学报，2002（1）：46-51.

［2］朱 浩 然.SIR 带 阻 滤 波 器 的 研 究［D］.合 肥：安 徽 大学，2010.

［3］杨维名，吴姣.基于分形技术的阶跃阻抗微带低通滤波器设计［J］.电波科学学报，2010（5）：1000-1004.

［4］微带滤波器谐波抑制的研究［D］.成都：西南交通大学，2010.

［5］吴志荣，李伟，林祀楠.微带SIR 带通滤波电路寄生通带的分析［J］.电路与系统学报，2003（1）：50-53.

［6］M.Makimoto，S.Yamashita.BandPass filter using Parallel coupled strip line stepped impedance resonators［J］.IEEETrans，1980：1413-1417.

［7］牛吉韬.微带SIR 滤波器研究［D］.成都：电子科技大学，2006.

［8］章晓卿，尹秋艳，杨小丽.分形微带带通滤波器的研究和设计［J］.舰船电子工程，2006（6）：140-142.

［9］李天鹏，王光明，梁建刚.新型Koch岛分形耦合微带线带通滤波器［J］.电讯技术，2011（3）：37-40.

［10］章晓卿.微波带通滤波器小型化研究和分形结构新型滤波器设计［D］.上海：华东师范大学，2006.