后向平滑平方根容积卡尔曼滤波算法及其应用

张 智，姜秋喜，潘继飞

（解放军电子工程学院，安徽 合肥230037）

0 引言

非线性滤波来源于含噪声观测值非线性系统的状态估计问题［1］，广泛应用于众多工程领域。其最优解需要对系统状态的后验概率分布进行完整描述，但这几乎是不可能实现的。因此，当前的研究着重于各种次优滤波算法。无迹卡尔曼滤波（Unscented Kalman Filter，UKF）［2-4］通过选取确定的加权采样点来逼近随机变量的概率分布，其不仅避免了雅克比矩阵的计算，还使精度至少达到二阶，优于扩展卡尔曼滤波及其衍生算法。而容积卡尔曼滤波（Cubature Kalman Filter，CKF）［5-7］是一种新型的非线性滤波方法，其利用等权值的容积点对后验概率密度进行近似，具有更好的估计性能。同时，相比于UKF，CKF无需选择任何参数，算法实现更加简单。其中，文献［3］利用状态方程对相邻时刻状态的约束关系以及量测更新，为再次前向滤波提供了更精确的初始值，从而提高了滤波算法的估计性能。文献［7］利用当前时刻的滤波结果，通过后向平滑得到上一时刻更加精确的状态估计值，并以此进行二次前向滤波，提高了滤波算法的精度和收敛速度。

然而，在单站无源定位的实际应用中，由于可观测性弱、观测噪声大以及数值计算舍入误差等因素影响，容易造成定位精度低、收敛速度慢和滤波性能不稳定甚至不能工作等问题。针对这些问题，本文在文献［3］及文献［7］的启发下，提出了后向平滑平方根CKF 算 法（Backward Smoothing Square-Root CKF，BSSRCKF）。

1 容积卡尔曼滤波算法

考虑如下离散时间非线性系统：

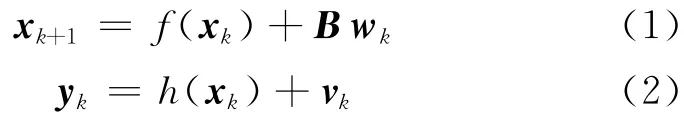
其 中，xk+1为系统状态向量，yk为观测值，f和h为非线性函数，B 为控制矩阵，wk和vk为零均值、协方差分别为Q 和R 的加性高斯白噪声。

容积卡尔曼滤波算法［5］由高斯域贝叶斯滤波理论推导而来，在该理论框架下，其可归结为非线性函数与高斯概率密度函数乘积的数值积分问题，即：

其中，g 为已知的非线性函数，Rn为积分区域，为权函数。

容积卡尔曼滤波采用三阶球面-径向容积准则，利用2n个容积点加权求和来逼近形如式（3）的加权高斯积分，即：

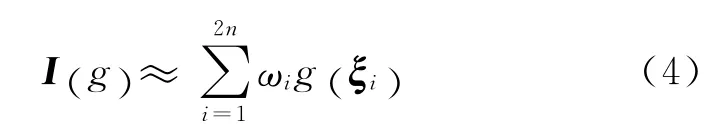
容积点ξi（i=1，2，…，m）及其对应的权值ωi（i=1，2，…，m）分别为：

其中，m=2n为容积点数，n为状态的维数。

2 后向平滑平方根容积卡尔曼滤波算法

2.1 基于Q-R 分解的SRCKF 算法

基于Q-R分解的SRCKF算法［6］采用误差协方差矩阵的平方根代替协方差矩阵进行递推运算，能够提高滤波算法的运行效率和数值稳定性。该算法的具体流程如下：

1）初始化，通过观测或其他先验信息确定初始的状态矢量^x0以及估计误差协方差矩阵的平方根S0，即：

其中，chol表示Cholesky分解。

2）时间更新

①估计容积点的值（i=1，2，…，m）：

②传播容积点：

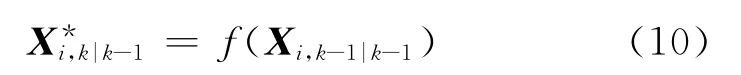
③计算状态预测值：

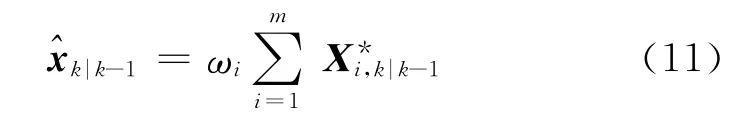
④计算状态预测误差协方差的平方根：

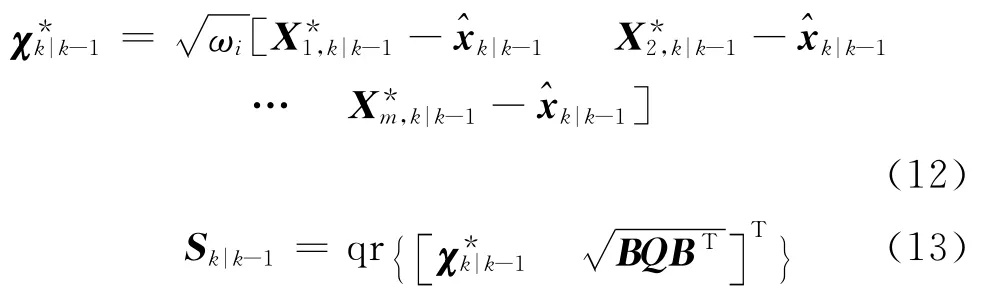
其中，qr表示Q-R 分解取下三角矩阵。

3）量测更新

①估计容积点的值（i=1，2，…，m）：

②传播容积点：

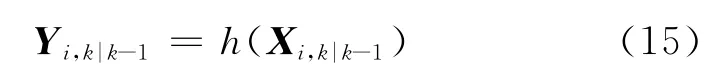
③计算量测估计值：

④计算矩阵T11、T21以及T22：

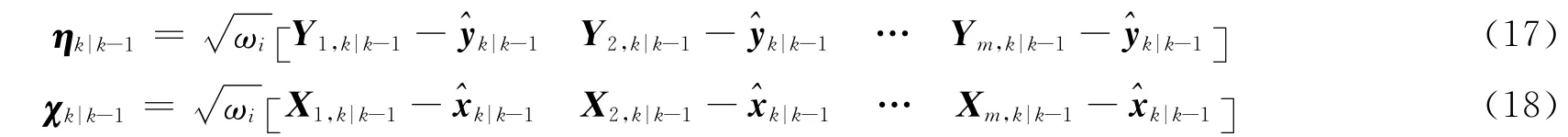
其中，d为观测量的个数，T11、T22分别为d×d维、m×m维下三角矩阵，T21为m×d维矩阵，0d×m、0m×d分别为d×m 维、m×d 维零矩阵。

⑤计算卡尔曼滤波增益：

其中，符号／表示右除。

⑥计算状态估计值：

⑦计算状态估计误差协方差矩阵的平方根：

2.2 基于Q-R 分解的后向平滑及量测更新

Rauch-Tung-Striebel（RTS）后 向 平 滑［8］是 一种固定区间平滑算法，采用递推的形式，计算简单、易于实现。其在前向滤波过程中，计算并存储系统的状态转移矩阵以及每一时刻的状态值、估计误差协方差矩阵，并以此作为后向平滑递推公式的输入值，从而获得最优的平滑估计结果。

然而，RTS后向平滑由于求取协方差矩阵时涉及两正定矩阵相减，有可能破坏协方差矩阵的正定性和对称性。故本文采用基于Q-R分解的RTS后向平滑算法［9］，使用协方差矩阵的平方根进行递推运算，提高了数值稳定性以及求逆运算的计算效率。

为了进一步改善算法的性能，本文在RTS后向平滑的基础上，利用上一时刻的观测值信息进行量测更新，并将获得的上一时刻更加精确的估计值作为第二次前向滤波的初始值，从而提高算法的精度和收敛速度。该算法的具体流程如下：

1）计算矩阵U11、U21以及U22：

其中，U11、U22为n×n维下三角矩阵，U21为n×n维矩阵，0n×n为n×n维零矩阵。

2）计算平滑增益：

3）计算平滑预测值：

4）计算状态预测误差协方差矩阵的平方根：

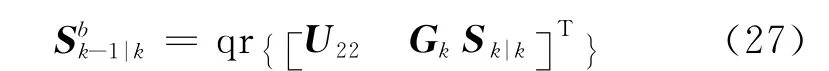
再根据式（15）— 式（22）进行量测更新，可以得到k-1时刻更加精确的

2.3 第二次前向滤波

综上所述，本文提出的后向平滑SRCKF 算法的实现流程如图1所示，其中①、②、③、④表示算法的运算顺序，其执行过程具体为：

1）当k≥1时，按式（7）—式（22）得到当前k时刻的状态估计值；

2）根据式（23）— 式（27）进行RTS后向平滑，得到k-1时刻的状态预测值；

本算法利用k时刻SRCKF的滤波结果通过后向平滑并利用k-1时刻的观测值进行量测更新，由于同时利用了k时刻与k-1时刻的观测值信息，其能够获得k-1时刻更加精确的状态估计值，以此作为初始条件再次进行前向滤波就能得到当前k时刻更加准确的估计值，提高了算法的定位精度与收敛速度。同时，采用Q-R分解的形式，并使用误差协方差的平方根进行运算，从而提高了新算法的稳定性与运算效率。

图1 后向平滑SRCKF算法流程示意图Fig.1 The operation process of backward smoothing SRCKF

3 单站无源定位仿真实验

3.1 状态方程与观测方程

观测站与目标辐射源的位置关系如图2所示，在三维直角坐标系中，k 时刻观测站O 的状态矢量为，目标辐射源T 的状态矢量为两者之间的径向距离为rk，方位角为βk，俯仰角为εk，相对运动状态矢量为xk=xTk-xOk= ［xk，yk，，以 目 标 辐 射 源 的 方 位 角βk，俯 仰 角εk，相位差变化率和多普勒频率变化率作为观测量，则系统的状态方程和观测方程可分别表示为：

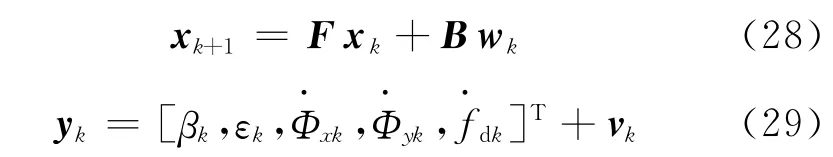
图2 观测站与目标的位置关系示意图Fig.2 Geometrical relation between observer and target

3.2 仿真实验及结果分析

假设在三维直角坐标系中，观测站固定于原点，目标辐射源的初始位置为（190，160，10）km，速度为（-280，160，0）m／s。为了验证BSSRCKF算法的性能，在不同的观测精度下将其同CKF、文献［7］所提出的BSCKF算法的性能进行对比，其中各组参数观测精度如下：在仿真实验中，观测周期T=1s，观测次数N=100，系统误差为wxk=wyk=wzk=1m／s2，辐射源信号的载频fT=10GHz，观测站中相互正交干涉仪的基线长度分别为dx=10m，dy=5m。采用相对距离误差（Relative Range Error，RRE）作为评价标准，每一组做100 次Monte Carlo实验，在定位结束时刻RRE＜15%，则视作本次实验收敛，否则视为发散。定位精度为跟踪结束时刻RRE的平均值，如表1、表2以及图3— 图5所示（剔除了不收敛的实验结果）。

其中，（xk，yk，zk）表示目标k时刻的真实位置表示目标k时刻位置的估计值。

表1 不同算法的定位精度与稳定性比较Tab.1 Comparison of algorithms locating accuracy and robustness

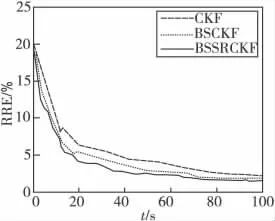
图3 观测精度1时，各算法的相对位置误差曲线Fig.3 Relative range error curves of each algorithm in measurement precision 1

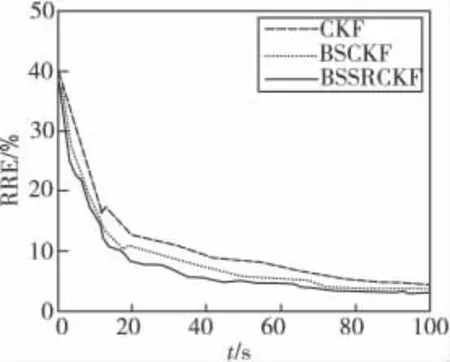
图4 观测精度2时，各算法的相对位置误差曲线Fig.4 Relative range error curves of each algorithm in measurement precision 2

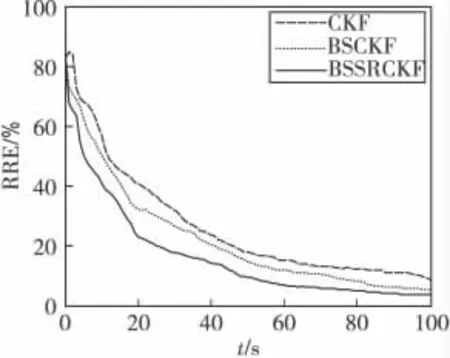
图5 观测精度3时，各算法的相对位置误差曲线Fig.5 Relative range error curves of each algorithm in measurement precision 3

从表1、图3—图5可以看出，在高精度观测时，各算法都能很快收敛，且定位精度都比较高，但随着观测精度的降低，各算法的定位精度开始下降，收敛速度变慢，且滤波发散的次数开始增多。相比之下，BSSRCKF的性能最好，其他依次为BSCKF 以及CKF，且在低观测精度时各算法的性能差别更明显。由图5 可以看出，当观测精度低时，由于BSCKF采用RTS后向平滑为二次前向滤波提供了更为精确的初始值，故无论是定位精度还是收敛速度都优于CKF。而BSSRCKF 在后向平滑的基础上，利用前一时刻的观测值进行量测更新，进一步提高了二次前向滤波的初始值，更加改善了定位的性能。

从表1可以看出，当观测精度降低时，BSCKF由于在后向平滑过程中两正定矩阵相减容易失去正定性与对称性，造成滤波结果发散甚至无法运行。而ISRUKFS采用Q-R 分解的形式，使用误差协方差的平方根进行递推运算，避免了正定矩阵相减的运算，故稳定性优于其他两种算法。

表2 不同算法的单次运行时间比较Tab.2 Comparison of algorithms single running time

在Intel酷睿双核，CPU 主频2.6GHz，内存2GB的计算机使用Matlab7.10运行各算法，分别得到单次运行时间如表2所示，可见由于BSCKF与CKF相比，增加了后向平滑和二次前向滤波，计算量是后者的2倍多。相比之下，BSSRCKF虽然采用了Q-R分解的形式，提高了运算效率，但增加的量测更新处理使得其计算量接近CKF的3倍。然而，在保证实时性的前提下，这种适当增加计算量来换取定位精度、收敛速度以及稳定性的较大改善是值得的。

4 结论

本文提出了后向平滑平方根容积卡尔曼滤波算法，并应用于单站无源定位领域。该算法利用当前时刻的滤波结果通过后向平滑算法得到上一时刻的预测值，并采用该时刻的观测值进行量测更新，为再次前向滤波提供了更加精确的起始值。同时，其采用Q-R 分解的形式，并使用误差协方差的平方根代替协方差参与滤波和平滑。仿真实验表明，该算法在满足实时性要求的基础上，提高了单站无源定位的精度、收敛速度以及稳定性。特别地，该算法是以增加算法复杂度的代价来提高性能，当对定位精度要求较高但观测精度较低时，在保证实时性的前提下，这种以增加计算量来换取定位精度的方法是可行的。因此，本文提出的算法对单站无源定位系统的研究具有一定的工程应用价值，同时也适用于其他非线性滤波领域。

［1］Ito K，Xiong K.Gaussian filters for nonlinear filtering problems［J］.IEEE Transactions on Automatic Control，2000，45（5）：910-927.

［2］Julier S J，Uhlman J K.Unscented filter and nonlinear estimation［J］.Proceedings of IEEE，2004，92（3）：401-422.

［3］张刚兵，刘渝，胥嘉佳.基于UKF的单站无源定位与跟踪双向预测滤波算法［J］.系统工程与电子技术，2010，32（7）：1415-1418.

［4］黄耀光，高博，李建新，等.基于平方根UKF双向滤波的单站无源定位算法［J］.数据采集与处理，2013，28（2）：207-212.

［5］Arasaratnam I，Haykin S.Cubature kalman filters［J］.IEEE Transactions on Automatic Control，2009，54（6）：1254-1269.

［6］Arasaratnam I，Haykin S，Hurd T R.Cubature kalman filtering for continuous-discrete systems：theory and simulations［J］.IEEE Transactions on Signal Processing，2010，58（10）：4977-4993.

［7］霍光，李冬海.基于后向平滑容积卡尔曼滤波的单站无源定位算法［J］.信号处理，2013，29（1）：68-74.

［8］Rauch H E，Tung F C，Striebel T.Maximum likelihood estimates of linear dynamic system［J］.AIAA Journal，1965，80（3）：1445-1450.

［9］Arasaratnam I，Haykin S.Cubature kalman smoothers［J］.Automatica，2011，47（10）：2245-2250.