带水平倾角的被动声定位双三角阵模型

狄长安，闵 想，刘新爱，边 鹏

（1.南京理工大学机械工程学院，江苏 南京 210094；2.中国科学院电子学研究所，北京 100190；3.北方华安工业集团有限公司，黑龙江 齐齐哈尔 161006）

0 引言

立靶精度（射击准确度和射击密集度）是身管武器考核时的重要技术指标，射击密集度一般用弹着点坐标的中间误差来表示［1］。当测试靶面超过2m×2m，在进行自动检靶时，一般采用声定位的方法检测弹着点坐标［2-3］。研究表明，声传感器布阵模型对弹着点坐标的检测精度影响较大，且随着靶面的增大，检测误差会进一步增大。目前，比较实用的水平双三角阵定位模型在有效靶面为10m×10 m时，定位误差可达±2cm［4］。但随着小口径炮弹着点的校验指标不断提高，对弹着点的检测精度提出更高的要求，±2cm 的定位误差已经不能满足立靶密集度测量要求。针对此问题，本文提出了带水平倾角的被动声定位双三角阵模型。

1 水平双三角阵定位模型

被动声定位水平双三角阵定位原理如图1 所示，在弹道的垂直方向上构建一个虚拟靶面，其中，传感器M1、M2、M3与M4、M5、M6分别构成两组等边三角形，并沿y 轴左右对称，M1、M3、M4、M6在同一直线上水平放置。当超音速弹丸垂直射入靶面时，会产生激波，并传至各声传感器，根据传感器M1～M6在坐标系中的相对位置以及弹丸激波到达各传感器的时间差，可建立被动声定位水平双三角阵定位模型：

式（1）中，p（x，y）为弹着点坐标，（xi，yi）、（xj，yj）为任意两个声传感器的坐标，ti、tj为激波到达对应声传感器的时间，vh为激波传播速度在靶面方向的分量。通过式（1）可展开成9个非线性方程，通过求解该非线性方程组可以得出弹着点坐标P（x，y）。

仿真计算及实验数据表明［4］，在靶面的中心区域的测试误差在±2cm以内，但边缘区域的误差相对较大；而且在安装过程中，还会人为的引入随机误差，这给传感器阵的定位精度与其稳定性造成一定的影响。

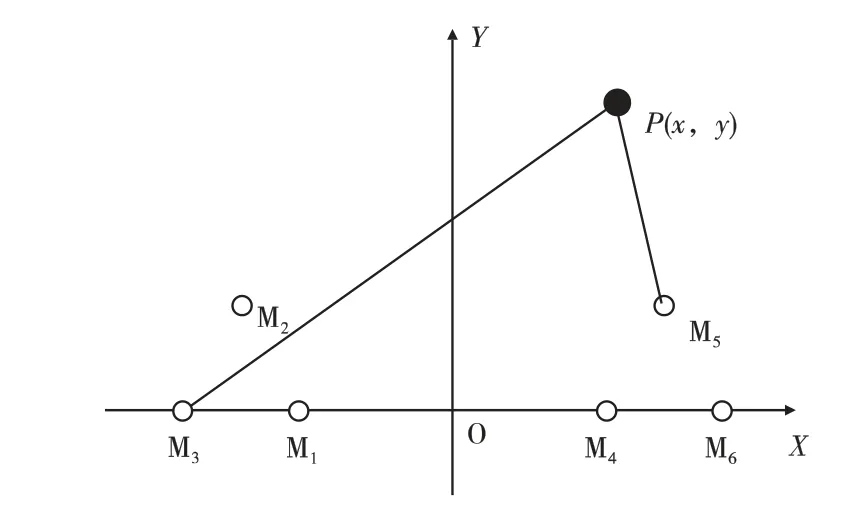
图1 水平双三角阵定位模型Fig.1 Location model of horizontal double triangle array

2 带水平倾角双三角阵定位模型

图1研究的是等边三角阵型的水平放置情况，当M1M3、M4M6与水平面存在一个夹角θ时，此时，水平双三角阵定位模型可转换为图2所示模型。

式（2）中，a为等边三角形的边长（基阵臂长），b为两三角形的半间距，θ为传感器阵与水平轴的夹角，t12～t16分别为弹丸激波到达声传感器M1与其他各传感器的时间差。

图2 传感器布阵示意图Fig.2 Diagram of sensors array

3 仿真计算与误差分析

非线性方程组的数值解法有多种，例如：微分方程数值解法、加权余量法、变分法。但针对本系统模型所建立的方程组，加权余量法中的最小二乘法（Gauss-Newton法）为最优算法，该算法根据系统的精度要求设定迭代次数［5］，在不影响计算精度的前提下可减少主控芯片的计算时间，因此本文采用最小二乘法，对定位模型进行仿真计算。

在大靶面的弹着点自动检靶系统中，测试精度随着测试范围增大而降低，因此，在进行仿真计算时，需要重点关注测试靶面的边缘区域的测试精度［6］。由于声传感器呈左右对称分布，测试区域也关于y 轴呈对称分布，因此只需要在第一象限进行仿真计算。沿着测试区域x轴方向，在0～5m 范围内，步进0.5m进行等间距划分；沿y轴方向，在1～11m 范围内，步进1m 进行等间距划分。划分后的测试区域网格，如图3所示，可分别对每个小的测试区域网格的边界点进行仿真计算分析。

在满足测试精度要求的前提下，考虑到声传感器安装尺寸、安全性对现场定位装置体积的要求以及安装运输的方便，设定声传感器沿x轴方向布阵的总长不超过2.5m，沿y轴方向的布阵总不超过0.5m。

1）当θ=0°，a=0.3m，b=0.7m时的水平双三角阵的定位精度为±2cm［4］。保持a=0.3 m，b=0.7m不变，θ在0～180°范围内连续取值，由于篇幅限制，仅给出如图4所示的具有代表性的θ的仿真分析结果（θ为25°、50°、75°、100°）。

图3 仿真测试点的分布图Fig.3 Distribution diagram of simulation points

图4 测量误差随θ变化的仿真图Fig.4 Simulation of measuring error variation byθ

图4表明：在y轴方向上，系统的测量误差随y值的增大成递增趋势，边缘的测试误差随着θ的增大呈先增后减、再递增的状态，其中θ=75°时误差最小。x 轴方向上，系统的误差大小相对比较平稳，但是θ=25°、100°时，边缘测试区域的测量误差相对较大，已逼近0.02m；当θ=50°，虽然在大部分区域的测试误差都在0.015m 以内，但在靶面的边缘区域测量误差较大；当θ=75°时，同一y 值对应各测试点的误差大小基本相同，而且最大的误差仅为0.013m，因此可基本确定θ取75°，相比普通的水平双三角阵的±0.2m 具有明显的提高。

2）确定了水平倾角后，为获取更高更稳定的测试精度，需重新对模型参数a、b的配比进行优化分析。考虑到传感器基阵的安装方便与精度，设定a+b=1m（水平方向布阵长度为2m），且a、b按照步进为0.1m 的变化，保持θ=75°不变，相关仿真结果如图5所示。

图5 测量误差随变化a、b的仿真图Fig.5 Simulation of measuring error variation by a and b

由图5的仿真结果表明，布阵模型的测试精度随着a／b的减小而增大，理论上优先考虑a=0.1 m，b=0.9m，但若a长度过小，会影响到传感器的安装精度，而且其误差曲线的斜率相对较大，将降低其稳定性能。因此选取a=0.2m，b=0.8m较为合适，此时，定位误差可控制在±0.012m 以内。

3）传感器支架加工以及安装传感器时均会引入误差，仿真时需考虑安装误差对测试系统精度的影响。由于a与θ 同属于一个构件，其精度可通过加工精度来保障，当a为0.2m 时，a的误差易控制在50μm，平面度控制在20μm 以内，此时，当基阵间距引入1mm 安装误差时相关仿真计算结果如图6所示。图6表明，定位误差可控制在±0.012m以内，可以满足测量精度要求。

图6 测量误差随安装误差变化的仿真结果Fig.6 simulation of measuring error change by installation error

4 结论

本文提出了带水平倾角的被动声定位双三角阵模型。该模型与水平双三角阵的区别在于三角基阵带有水平倾角，并且模型的各项参数都得到了进一步优化。在合理地选择模型参数的情况下，能在10 m×10m 的有效测试靶面内能获得更高的测试精度。仿真计算结果表明：当水平倾角θ为75°时，臂长a为0.2m、基阵间距2b为1.6m 的双三角阵的测试效果最佳，弹着点测试误差从普通水平双三角阵的2cm 减少至1.2cm。

［1］肖峰，李惠昌.声，武器和测量［M］.北京：国防工业出版社，2002：7-10.

［2］Zhang Jinsong，Walpola Malaka，Roelant David，et al.Self-organization of unattended wireless acoustic sensor networks for ground target tracking［J］.Pervasive and Mobile Computing，2009（5）：148-164.

［3］张飞猛，战延谋，周刚峰，等.声学立靶弹着点测试数学模型与误差分析［J］.应用声学，2006，25（4）：252-257.

［4］蒋东东.基于被动声定位的大靶面弹着点坐标测量方法研究［D］.南京：南京理工大学，2011.

［5］薛 毅.数 值 分 析 与 科 学 计 算［M］.北 京：科 学 出 版社.2011.

［6］蒋萍，狄长安.基于声学立靶的传感器阵列模型研究［J］.火炮发射与控制学报，2011，（4）：38-40.