初速跳动量对单兵火箭弹引信定距精度影响

洪 黎，张 合，李豪杰，唐玉发

（南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094）

0 引言

进入21世纪以来，世界形势和作战对象的变化，反恐战争、特种部队作战、地区性局部冲突己经成为重要的战争形式。单兵火箭弹由于体积小、重量轻、携带方便，非常适合这些作战模式［1-3］。

单兵火箭弹炸点精度直接影响其作战效能，而影响单兵火箭弹炸点精度因素包括初速、射角、地面温度、风向与风速等［4］。由于单兵火箭弹，以计时作为炸点依据，所以初速变化直接影响引信定距精度。单兵作战距离较近，弹丸接近直射发射，所以射角影响炸点精度较小。地面温度，主要影响发射药温度，从而影响初速变化。由于单兵火箭弹作用时间短，所以风对弹丸炸点影响较小。综上所述，各影响因素中，弹丸初速是炸点精度的主要影响因素之一。

文献［5-7］指出由于每发弹的发射药、发射环境等的不同，造成弹丸实际初速与标定初速之间存在偏差，这个偏差导致弹丸实际炸点偏离由标定值计算得到的理论炸点。文献［8］研究了初速跳动对榴弹的定位精度的影响，指出要保证榴弹的杀伤效果，应尽可能减少初速跳动量。而单兵火箭弹同样存在初速跳动量大的问题，国内外关于初速跳动量对单兵火箭弹引信作用时间的准确性的影响，即初速跳动量对引信定距精度的影响，未见相关报道。为此，本文分别研究未测速修正引信在不同射程上初速跳动量对定距误差的影响以及测速修正引信在不同射程上初速跳动量对定距误差的影响。

1 弹道模型与定距精度影响因素

1.1 弹道模型

1.1.1 火箭弹弹道方程

该火箭弹采用肩扛发射，定射程引爆，射程范围30～700m，炸高距地面2m 左右实现空炸，速度约为170m／s，转速低于60r／min。为建立六自由度弹道方程，特作以下假设［9-11］：

1）地表面为平面，忽略地球曲率影响；

2）弹体为刚体，忽略弹性；

3）地面坐标系为惯性坐标系；

4）攻角时刻为0。

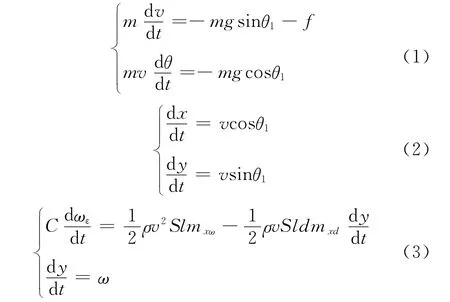
以上各式中：f 表示弹丸在飞行中所受到的空气阻力，V 表示弹丸运动速度，表示弹丸射角，t表示弹丸飞行时间，x 表示弹丸射程，y 表示弹丸高度，其他变量表示可参考文献［10］。

由空气动力学：

式中：ρ表示空气密度；V 表示弹丸质心相对于空气的速度；Sm表示弹丸最大横断面面积；M 表示马赫数；Cx0（M）阻力系数。

用雷达测出模拟弹外弹道，测算出该弹丸的阻力系数为0.45，则：

1.1.2 方程求解

求解外弹道方程的初始条件，由火箭弹的初速V0、射角θ0确定，应用数值方法求解常微分方程组，可计算出该单兵火箭弹在不同初速、不同射角和各种气象环境参数下外弹道参数的数值解［8］。当取f=7.308×10-4V2、初速V0=170m／s，所得到的外弹道有关参数分别列于表1。表中：x表示射程，θ0表示射角，tr表示飞行时间，h表示火箭弹炸高。

表1 射角、飞行时间、炸高与射程的关系Tab.1 The relationship between fire angle，time of flight，burst height and range

1.2 测速原理

弹丸及火箭筒示意如图1所示，在非金属发射筒上轴向布置两组磁铁，通过弹上感应线圈测得速度［6-7］。

图1 弹丸及火箭筒示意图Fig.1 The schematic diagram of projectile and rocket launcher

1.3 修正原理

当引信测得速度V 后根据射程相等的原则，用弹丸的飞行时间与速度的倒数成正比进行修正，修正公式为式（6）［12-13］，引信根据修正后的飞行时间点爆弹丸，从而实现精确击中目标。

式中：V0为弹丸理想初速，V 为弹丸实际初速，tr为引信理想初速时弹丸飞行时间，t为修正后弹丸飞行时间。

1.4 测速精度对炸点的影响

由于弹丸出炮口的速度是由两组磁铁之间的距离L 和弹丸飞经这段距离的时间t，通过公式V =L／t求得，所以测速精度分析设计涉及这两个参数，测速精度影响因素主要包括：磁铁磁场分布、磁铁安装精度、测速计时误差等。由于弹丸实际作用时间是根据测得速度对理论作用时间进行修正后所得［13］，所以测速精度是炸点散布大小的关键因素之一。

2 初速跳动量对定距精度的影响

该单兵火箭筒用激光火控系统对目标测距，弹道计算机根据目标距离、设计初速V0及气象条件，解算出火箭筒的射角θ0及飞行时间tr，射手根据解算出的θ0调整火箭筒的射角，飞行时间tr装定计时引信，发射后引信根据测得速度对飞行时间进行修正，引信计时到修正后的飞行时间即点爆弹丸。因此，该火箭弹定距精度影响因素包括：瞄具精度、引信计时精度、初速跳动量、弹道模型等，初速跳动量是影响定距精度的关键，假设其他因素不影响弹丸定距精度，火箭弹发射时的初速是设计初速，则按照表1所列的射角发射，无论有没自适应测速修正，引信都能保证弹丸在装定的射程处爆炸。然而在实际发射时，各发火箭筒发射药及燃烧状态存在差异，使火箭弹初速在一定的范围内跳动，以下利用MATLAB仿真分析初速跳动量对未测速修正和测速修正单兵火箭弹引信定距效果的影响。

2.1 初速跳动量对未测速修正引信定距误差的影响

根据设计的初速和射程，取表1中的射角，当初速V0从160～180m／s变动时，可得到一系列火箭弹的实际飞行轨迹。再用表1中的飞行时间tr作为确定弹丸起爆依据，可以计算出实际起爆点的位置，并与设计射程比较即可得到未测速修正火箭弹偏离预定起爆点的定距误差，如表2所示。

表2 不同射程时未修正单兵火箭弹定距误差与初速的关系Tab.2 The relationship of distance error of shoulder-fired rocket with no correction and initial velocity on different range

2.2 初速跳动量对测速修正引信定距误差的影响

假设自主式测速误差为±2m／s（根据实际测速试验结果所得），那么实际初速由测速值V1基础上加上±2m／s以内的随机变量所得，当测速值V1从160～180m／s变动时，根据设计射程和实际初速，取表1中的射角θ0，可得到一系列火箭弹的实际飞行轨迹。根据表1中的引信飞行时间tr，再根据修正公式（6）对tr进行修正，得到修正后的引信飞行时间t作为确定弹丸起爆依据，可以计算出实际起爆点的位置，并与设计射程比较即可得到测速修正后火箭弹偏离预定起爆点的定距误差，如表3所示。

2.3 仿真结果分析

从表2、表3中列出的数据可见，由于初速的变化，未修正和修正后的火箭弹炸点位置误差均存在，而该单兵火箭弹的破片杀伤半径为10 m 左右，通过未测速修正和测速修正的定距状况比较，可得出以下结论：

1）未测速修正引信炸点平均误差随着射程的增大和初速跳动量的增大而增大，在射程为800 m时，不同的初速跳动量下的平均炸点误差达到了21.61m，在初速为160m／s和180m／s时，在不同的射程下的平均炸点误差分别达到了23.45 m 和23.42m，超过了弹丸杀伤半径，定距误差较大；

2）测速修正引信在不同射程时的炸点平均误差随着初速跳动量的增大而几乎保持不变，而不同速度跳动量时的炸点平均误差随着射程的增大而增大，在所有射程范围内，在160～180m／s初速跳动量下炸点误差随射程和初速的变化均保持在很小的值，误差范围为-7.24～7.35m，定距误差较小。

表3 不同射程时自适应测速修正后单兵火箭弹定距误差与初速的关系Tab.3 The relationship of distance error of shoulder-fired rocket with adaptive correction and initial velocity on different range

3 试验验证

3.1 靶场测速试验

实弹回收试验共进行了5 发，通过软件回读回收弹丸引信单片机Flash中采集到的速度数据，整理后与激光靶测得的炮口速度进行对照，试验结果如表4所示，速度散布在±2m／s以内，满足引信系统测速精度指标。

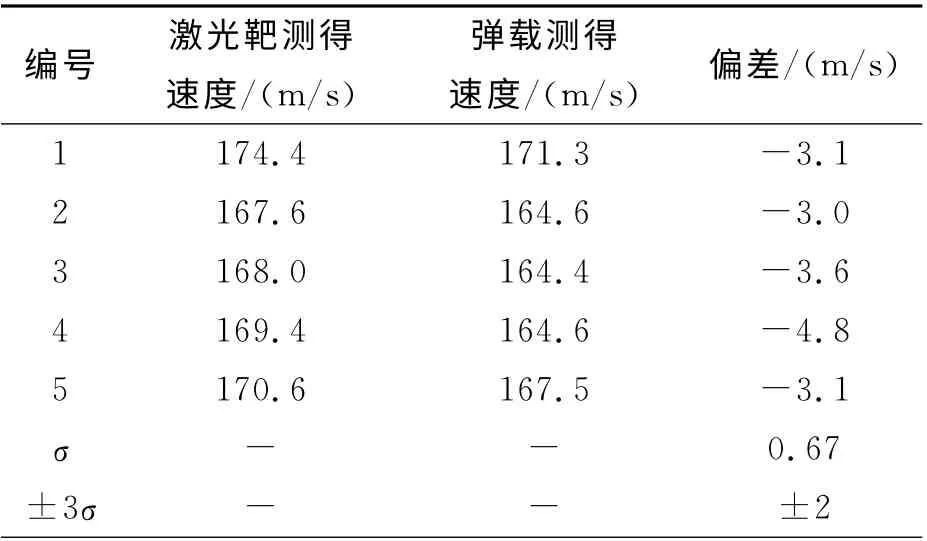
表4 测速结果Tab.4 Velocity measurement results

3.2 靶场空炸试验

3.2.1 试验过程

靶场实弹试验如图2和图3所示，图2中试验设备包括激光瞄具、火箭筒、发射架、激光靶等，图3是测速修正弹丸炸点图，图中亮光表示火箭弹爆炸瞬间发出的火焰，图中显示4根标杆，标杆从左到右依次表示：390 m、395 m、400 m、405 m，炸点为397.1m。

试验过程：射手根据激光瞄具及弹道计算机解算出的射角θ0调整火箭筒射角，将解出的飞行时间tr装定引信，装定成功后发射弹丸，未测速修正火箭弹根据装定的飞行时间点爆弹丸，或测速修正火箭弹加速运动至两组磁铁时进行自主式测速，进而根据所测速度对引信飞行时间进行修正，引信根据修正后的飞行时间点爆弹丸，同时弹丸经过激光靶时启动激光靶计时测速，得到各发弹丸实际初速。

图2 试验设备Fig.2 Trial equipment

图3 实弹空炸Fig.3 Live air-burst

4 结论

3.2.2 试验数据处理

空炸试验共发射10发火箭弹，10发弹丸均定距在400m 位置处空炸，5发未测速修正弹丸结果如表5所示，5发加测速修正弹丸结果如表6所示，比较结果：未测速修正引信炸点均值396.44 m，标准差为12.34，总体散布在±5 m 范围的概率为0.34；测速修正引信炸点均值399.48 m，标准差为2.25，总体散布在±5m 范围的概率为0.97。说明初速跳动对未测速修正引信炸点误差影响较大，而对测速修正引信的炸点误差影响较小。

表5 未测速修正弹丸试验结果Tab.5 Trial results of of shoulder-fired rocket with no correction

表6 测速修正弹丸试验结果Tab.6 Trial results shoulder-fired rocket with adaptive correction

本文采用MATLAB仿真分析了初速跳动量对未测速修正引信和测速修正引信定距误差的影响。得到初速跳动量对未测速修正引信炸点精度影响较大，而对测速修正引信的炸点精度影响较小，但是误差随着射距增大的规律不变的结果。实弹空炸试验结果与仿真得出的规律相同。因此，为了保证火箭弹炸点精度，对于未测速修正引信弹丸，尤其针对远距离目标应尽可能减小初速的跳动量；对于测速修正引信弹丸，可大大降低对初速跳动量的控制要求，而炸点精度仍可达到较高指标。由于该型单兵火箭弹初速跳动大，为了保证炸点精度，单兵火箭弹引信应当加测速修正。

［1］贠来峰，芮筱亭，冯可华.平衡抛射武器内弹道性能研究［J］.南京理工大学学报，2009，33（2）：258-271.

［2］隋高山.单兵火箭新型发射原理初步研究［D］.南京：南京理工大学，2009.

［3］贠来峰，芮筱亭，陈涛.一种平衡抛射单兵反装甲武器发射装药低温发射安全性分析［J］.兵工学报，2010，31（4）：429-433.

［4］闵杰，郭锡福.实用外弹道学［M］.北京：兵器工业部教材编辑室，1989.

［5］王利.弹丸炮口被动测速方法的研究［J］.弹道学报，2001，13（2）：79-83.

［6］纪霞，沙文龙，王利.感应装定中炮口速度测定方法研究［J］.弹箭与制导学报，2004，24（5）：542-544.

［7］朱莹，李永成，朱松柏.弹丸测速装定技术［J］.武器装备自动化，2006，25（6）：22-24.

［8］徐万和，张越，吴志林.初速跳动对班组武器引信定位精度的影响［J］.火炮发射与控制学报，2003，11（4）：26-32.

［9］侯宏录，王赛，闫帅.弹道参数对弹丸落点的影响分析［J］.西北工业大学学报，2009，29（3）：209-213.

［10］徐明友.火箭外弹道学［M］.哈尔滨：哈尔滨呢工业大学出版社，2004.

［11］孟新宇，王晓鸣，方清.6自由度修正弹道脉冲推力仿真研究［J］.系统仿真学报，2006，18（9）：2657-2660.

［12］陈萍.电子时间引信的计转数弹载测速自修正技术［D］.南京：南京理工大学，2007.

［13］洪黎，张合，李豪杰，等.某单兵火箭弹作用时间自适应修正方法［J］.仪器仪表学报，2013，34（8）：1916-1920.