筑形态创建中的几何方法——经典二维不可定向流形在E3 中的浸入
黄志斌 张群力 黄 俊 蒋 辉
(浙江省建筑设计研究院,杭州 310006)
1 概述
正如皮特·赛纳在他的著作【异质空间】中所评论的,“建筑正在重塑自身,参与到对拓扑几何的研究中去,参与到机器人材料生产的交响乐中,参与到生成、动力学塑造空间中去”。几何的定义非常广泛,按Riemann 的观点几何是由度量决定的,Klein 则提出了用变换群(代数方法)对几何分类的观点。二种观点在法国大几何家E.Cartan 提出联络观点以后得到了统一。拓扑学最初是几何学的一个分支,研究拓扑形体上与连续性质有关而与度量性质无关的问题。按Klein 的观点,拓扑学就是研究流形在连续变换下保持不变的性质的一种几何。因而拓扑学研究的问题更为本质也更抽象。流形上的拓扑结构是本质的,但度量结构则是附加的。拓扑流形是一种柔软、弯曲的形体或空间。建筑师在大脑中构思建筑的形态时,就自然地在运用流形的方法进行思维了,在他脑海里所呈现出的拓扑形体就是流形。他可以运用拓扑方面的经验与知识进行抽象的思维。一旦该拓扑形体思考成熟后就采用草图的方式勾画在白纸上。接下来就是要将这个拓扑流形(柔软的)嵌入或浸入到E3中来(赋予其欧氏度量)成为几何模型(硬的)。M˙obius带、Klein 瓶、实射影平面是连通、紧致、不可定向的二维流形。M˙obius 带是开流形,Klein 瓶、实射影平面是闭流形。受视觉功能限制,我们无法看到嵌入在高维欧氏空间中的Klein 瓶和实射影平面。但可以看到它们在E3中的浸入子流形。这些子流形有着丰富的几何、拓扑结构,是非常理想的造型曲面。拓扑学中的概念较为抽象,本文采用形象思维与抽象思维相结合,直觉与逻辑相结合的方式展开讨论。
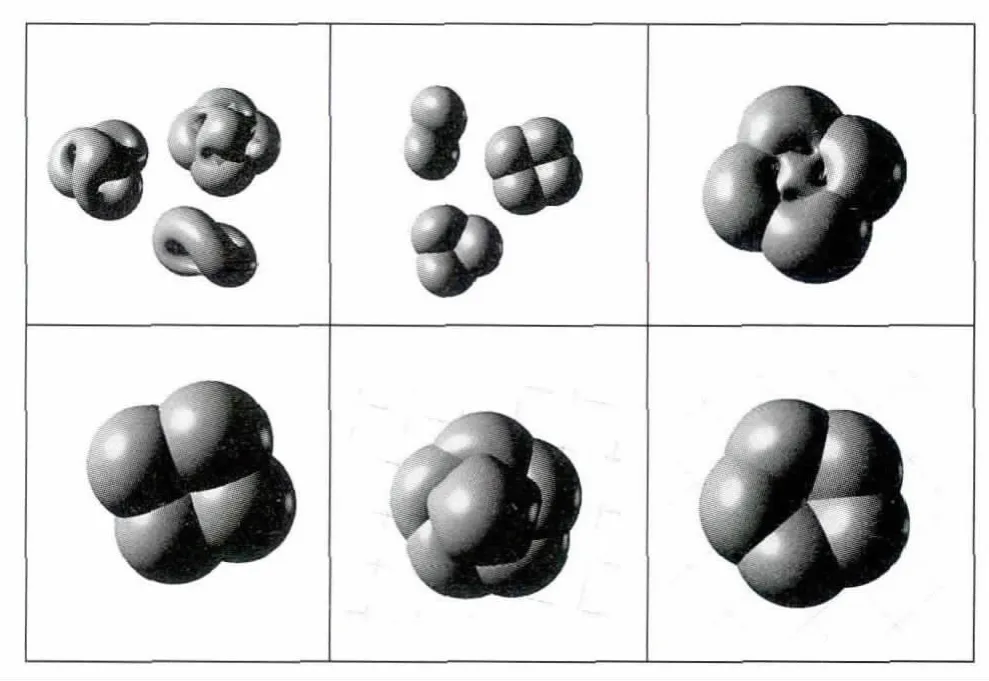
图1 不同旋转对称的Boy's 曲面
2 流形与闭曲面拓扑分类
2.1 流形简介
流形的概念是欧氏空间的推广,同时也是曲线曲面的抽象。欧氏空间是一种最简单的流形。拓扑学一般关心流形的整体(宏观)性质,而古典微分几何关注流形的局部(微观)性质。由流形上的高斯-博(Gauss -Bonnet)公式可知:流形的局部几何性质与流形的整体拓扑性质是密切相关的。用流形的方法来讨论问题的好处之一就是可以从整体上讨论几何、拓扑间的关系。一般来讲凡是可以参数化的几何形体都是流形,例如NURBS 曲线、曲面,解析曲线、曲面,欧氏空间等等。
2.2 子流形的浸入与嵌入
嵌入、浸入:设M 和N 分别是m 维和n 光滑流形。若存在光滑映射F:M →N,使得:对∀p ∈M,映射F 均为满秩的,即rank(F)=m ≤n,则称F 是M 在N 中的一个浸入,而称M 在F下为N 的一个浸入子流形,记为(F,M)。映射F 为满秩的条件下是单一映射,则称F 是M 在N中的一个嵌入,(F,M)为N 的一个嵌入子流形。浸入在局部是单一的映射(这一点由满秩决定),但是在大范围则不一定单一。因此,浸入子流形和嵌入子流形的区别在于像集F(M)在N 中是否有自交点。
2.3 流形的定向性
曲面(或二维流形)的定向性是曲面的整体、内在的拓扑性质。曲面(或二维流形)上的法向量从任一点出发,沿着曲面上任一闭曲线回到原处时法向量的方向若不变时称该曲面(或二维流形)是可定向的。法向量的方向若变成相反时称该曲面(或二维流形)为不可定向的。
2.4 拓扑粘合
在现实的物理时空中,建筑师会用一些小纸片涂上胶水粘出复杂的模型,或者用建筑模型材料搭出复杂的建筑模型。在抽象的拓扑空间里则可以用内蕴的方法对拓扑对象——流形进行类似操作。拓扑粘合(商映射)的方法是一种内蕴的方法,与外围空间无关,对每一个粘合过程不必考虑是否能在欧氏空间中的实现问题。商映射就是粘拓扑空间的胶水。它让我们可以去刻画以前无法想象的复杂空间,把它们分解成简单直观的小块,并为分解和重新组装等操作提供严谨可靠的拓扑解释。例如:将二个有界二维流形——圆盘(圆盘中部想象为可以突起),沿着它们的边界(一维子流形——圆)上对应点粘合起来,可以得到一个二维闭流形——二维球面,这就是我们生活的现实世界——地球的拓扑模型。将二个三维流形——球体沿着它们的边界(二维子流形——球面)上对应点粘合起来,可以得到一个三维闭流形——三维球面,这就是Poincar˙e 所猜想的宇宙的拓扑模型。
2.5 闭曲面拓扑的分类
闭曲面分类定理:任何闭曲面必同胚于或球面,或者球面挖掉有限多个圆盘添上环柄,或者球面挖掉有限多个圆盘而补上M˙obius 带。这些曲面中的任意两个是不同胚的。在一个球面上挖掉n 个圆盘,再粘上n 个环柄后就得到闭曲面Mn,称为亏格数为n 的可定向曲面,显然M1就是圆环T1。而在一个球面上挖掉n 个圆盘,再粘上n 个M˙obius 带后就得到闭曲面Pn,称为亏格数为n 的不可定向曲面。当然这种粘帖在E3空间无法具体实现。用曲面拓扑中的粘贴空间(商空间)法,可以证明P1就是实射影平面。而P2就是Klein 瓶。根据曲面拓扑学,E3空间连通、紧致的闭曲面可按亏格数分类:球面亏格数为0,剩下来亏格数为正的(可定向的)一半是环面T1、双环面T2……Tn;亏格数为负的(不可定向的)一半是实射影平面RP1、Klein 瓶、P2……Pn。M˙obius 带是开流形,Klein 瓶、实射影平面是闭流形。与可定向的曲面相比不可定向曲面有着更丰富的几何、拓扑结构。

图2 二维紧致闭可定向曲面的拓扑分类,亏格数依次为0,1,2,3(网络图片)
3 莫比乌斯(M˙obius)带与建筑造型
M˙obius 带是二维不可定向的开流形,它可以嵌入到E3中。任何一个二维流形只要其上局部有M˙obius 带,那么这个二维流形就是不可定向的。它的一个简单的拓扑模型是,将一个长方形纸条的一端固定,另一端扭转180 度后,粘合在一起,得到的曲面就是M˙obius 带。

图3 M˙obius 带的基本多边形

图4 带M˙obius 在E3 中的一种嵌入

图5 全球首座带M˙obius 造型的三D 打印建筑将于2014年诞生,由荷兰与德国工程师携手制造(网络图片)

图6 M˙obius 住宅,韩国设计师设计图

图7 M˙obius 塔BAU 建筑事务所

图8 M˙obius 带造型
4 克莱因(Klein)瓶与建筑造型
Klein 瓶是二维不可定向的亏格数为-2 的闭流形。Klein 瓶记作P2,它和环面T2都可以用一截圆柱面将两个截口相互粘接得到。如果每一直母线的两端粘合,得到的是环面,此时两个截口是以相同的方相粘接的。如果让两个截口方相相反地粘接,得到的就是Klein 瓶。要实现这样的粘接,必须将圆柱面弯曲后,把一端穿过管壁进入管内与另一端相接。在E3中这是做不到的,因为在进入管内之处必然要相交。但在E4中可以实现(让相交点的第四个坐标不同,从而把它们分开)。另一种构造方法是,从一个球面挖去二个圆盘,并在此处添上二个M˙obius 带,M˙obius 带的边缘是由一个整圆周构成,将这个圆周与球面上所开洞的边界圆周粘起来便可。这样得到的闭曲面就是Klein 瓶。

图9 Klein 瓶的基本多边形

图10 Klein 瓶在E3 中一种经典浸入

图11 2010 年上海世博会 委瑞内拉馆Klein 瓶造型(网络图片)

图12 Klein 瓶在E3 中的经典浸入
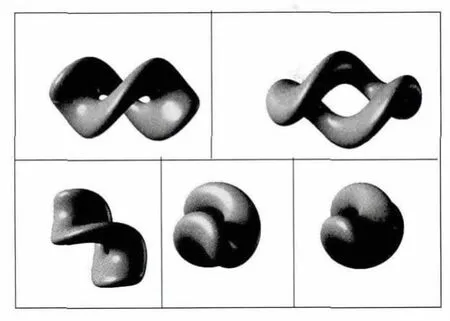
图13 8 字Klein 瓶在E3 中的浸入
5 实射影平面与艺术造型
5.1 实射影平面简介
实射影平面是二维不可定向的亏格数为-1 的闭流形。实射影平面记作RP1,它是射影几何中的概念。拓扑学中,有几种描述它的方法:1)将矩形的两对对边按相反的方向粘合起来;2)把圆盘的边界上每一对对径点粘合起来;3)从一个球面挖去一个圆盘,并在此处添上一个M˙obius 带,M˙obius 带的边缘是由一个整圆周构成,将这个圆周与球面上所开洞的边界圆周粘起来便可。这样得到的闭曲面就是实射影平面(该过程中,不使自己相交的粘合最低维数的欧氏空间是E4)。实射影平面是无法嵌入到E3中的,但可以浸入到E3中,图18 给出了实射影平面到E3中的几种经典浸入的图形。实射影平面到E3中的最佳浸入是由数学家伯伊给出的,通常称其为Boy's 曲面。其造型独特、十分优美是理想的建筑造型曲面。

图14 Klein 瓶在E3 中的浸入的不同变异
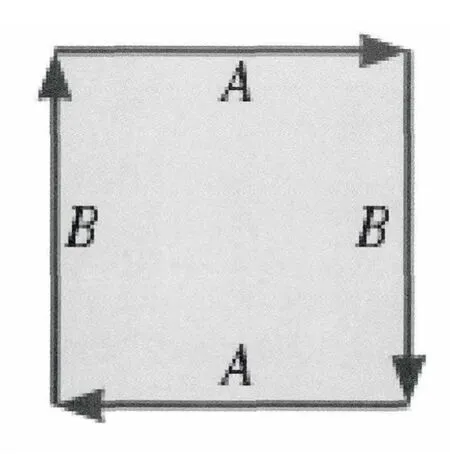
图15 实射影平面的基本多边形

图16 实射影平面在E3 中的最佳浸入Boy's 曲面

图17 德国上沃尔法赫数学研究所大门内的Boy's 曲面雕塑

图18 其几种实射影平面在中的经典浸入,这些看上去不太相同的曲面,其实就是同一个拓扑空间RP1 (实射影平面)在E3 中的不同浸入,不过它们有着相同“内蕴”的拓扑结构
5.2 Boy's 曲面的绘制
利用复平面上的圆盘到E3中极小映射(Weierstrass表示),得到叶轮状极小曲面。再将叶轮状极小曲面边缘上的对径点“粘合”起来,就得到了Boy's 曲面。
第一步:取复平面上单连通的单位圆域为定义域D,复变量z 采用极坐标形式z=reiθ,得参数变动范围为D:0 ≤r ≤1;0 ≤θ <2π。
第二步:由极小映射

计算出三叶状极小曲面上离散点的三维空间坐标(x,y,z),利用Rhino 软件绘制出它的NURBS 曲面(图19)。

图19 三叶状极小曲面
第三步:粘合边界上的对径点得到Boy's 曲面,具体就是用下式:
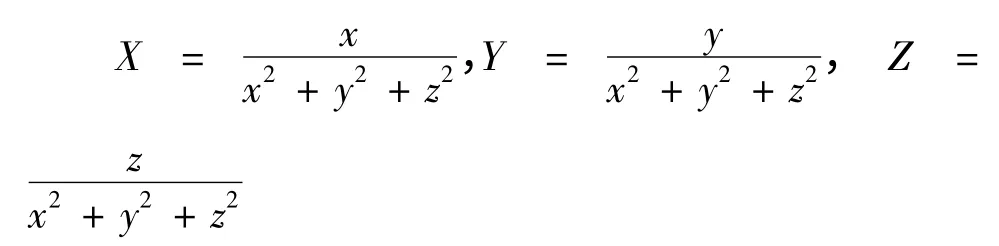
计算出120 度旋转对称的Boy's 曲面上离散点的三维空间坐标(X,Y,Z),最后绘制出它的NURBS 曲面(图20)。图中可以看到,Boy's 曲面在R3中是自交的,因此它是E3的浸入而不是嵌入。另外Boy's 曲面是由极小曲面做粘合映射而得,但它不是极小曲面。

图20 Boy's 曲面

图21 Boy's 曲面同胚变换

图22 Boy's 曲面空间网格造型
6 结语
人类是只能观察三维物体的生物,我们在镜中看到自己的图象是三维物体在二维空间的投影。同样地,通常人们展示的Klein 瓶、实射影平面的实物模型只不过是它们在E3中的某一种浸入而已(模型上都有一部分和另一部分重叠交叉)。真正的克莱因瓶、实射影平面都是二维不可定向的流形。是柔软的拓扑形体而不是刚硬的几何形体。它们只能嵌入到E4中。因此只能进行想象却又无法看到的。事实上,那些用现实建筑方式表现的克莱因瓶、实射影平面也只是采用了它们在E3中浸入的某种浸入的造型,建筑师只是从中获得概念性的启示。同时从这些不同浸入的造型以及它们的拓扑变形中获得理想的建筑形态。建筑形态一般是基于欧氏几何的,现在逐步出现了一些基于非欧几何、流形几何的倾向。这反映了当代技术、科学、哲学和美学的发展。当然这一切源自于思想的解放、观念的更新和技术的提高。
[1]当代西方建筑形态数字化设计的方法与策略研究.天津大学高峰学位论文.
[2]包志强.点集拓扑学与代数拓扑学引论.北京:北京大学出版社,2013.9
[3]王丹.非欧几里德倾向.厦门大学学位论文
[4]刘滨.拓扑学在当代建筑形态与空间创作中的应用.天津大学学位论文
[5]李娜.空间网格结构几何形态研究与实现.浙江大学学位论文
[6]ROB KUSNER CONFORMAL GEOMETRY AND COMPLETE MINIMAL SURFACES BULLETIN(New Series)OF THE AMRICAN MATHEMATICAL SOCIETY.1987,17(2)
[7]E.加当著,姜立夫等译.黎曼几何学科学出版社.北京:1964 年11 月
[8]彭家贵,程卿.微分几何高等教育出版社.北京:2006(08)
[9]李修成,郭瑞芝,崔登兰.微分流形基础科学出版社.北京:2011.(07)
[10]张群力,周平槐,何银丰,程健.基于软件Rhino 的异型建筑几何造型.杭州:浙江建筑2013(03).

