滑坡失稳的断裂机制研究

王学军 邹启红

(重庆607勘察实业总公司，中国 重庆 400056)

滑坡是指斜坡或边坡表面岩土体沿着某一破坏面向前发生位移的地质地貌现象及动力学过程，工程上称为不良地质现象，它是一种全球泛生型重大地质灾害，据国土资源部发布的全国地质灾害通报表明，近十年来我国每年产生滑坡灾害平均10000次以上，况且滑坡发生时往往带来惨重的损失，轻则阻断交通，重则掩埋房屋造成大量的人员伤亡，如2014年6月30日上午9时许，云南省福贡县腊吐底村俄玛底木本尼发生重大山体滑坡灾害，造成15人失踪、3人受伤，交通中断，经济损失巨大；2013年1月11日云南省昭通市镇雄县果珠乡高坡村发生山体滑坡，近10余户村民住房被掩埋，遇难人数达20人。因此，进行滑坡失稳机制研究不仅有其科学价值，更有实际工程价值，尤其在当今构建和谐社会的大环境下，关注人民生命财产安全显得尤为重要。

针对滑坡失稳方面的课题，国内外公开发表的成果较多，有的也写进了相关规范中，如对于地方性的规范准则，重庆市地方标准《地质灾害防治工程设计规范》[1]中给出了滑坡稳定性系数计算方法，并提出了一些常用的防治工程手段；对于暂时还没写进规范的研究成果也具有潜在实用价值，如周福川、王小委从断裂力学角度推导了土质滑坡锚杆受拉位移解析表达式，并对某实际工程案例做了计算分析，理论计算结果与实测值相近，显示了理论计算公式的实用性[2]；朗惠芳、代彤认为岩质滑坡失稳往往是节理裂隙发育所致，滑动面岩桥在没有达到岩石抗剪屈服强度的条件下就已经屈服，从而导致滑坡失稳[3]；赵队家等以平面旋转滑坡为研究对象，认为该类滑坡形成模式包括：下部压密变形—中部牵引蠕动—后缘引张拉裂等过程[4]；程谦恭、胡厚田将侧翼锁固平面旋转滑坡变形模式概化为横向均布荷载与轴向受压组合变形的悬臂梁模型，从能量角度导出了滑坡稳定性系数的解析表达式，从而定量验证了平面旋转滑坡的动力学机理及稳定性判据；吴永等关注暴雨这一诱发滑坡的最重要因素，通过算例分析发现震后受损岩坡的裂缝存在一个可在裂隙水作用下自行扩展、贯通软弱夹层的临界深度，同时也存在一个决定滑坡体稳定与否的软弱夹层渗水区域极限长度；王宝亮等认为滑坡发育机制的核心是滑动带在压剪荷载作用下的断裂扩展，同时采用极限平衡理论和断裂力学理论建立了滑坡破坏机制的力学分析方法，分析方法运用于三峡库区故陵滑坡中，效果良好。

本文拟在前人研究成果的基础上，深入开展滑坡失稳的断裂机制研究，以期滑坡稳定性分析能更进一步定量化，从而推动减灾学科的发展。

1 滑坡失稳机制初探

不同的野外地质环境造就了不同形态的滑坡，进行滑坡失稳研究首先就是要进行滑坡野外识别工作，从而形成了不同的滑坡分类标准，如按滑坡体积分类、滑坡厚度分类和滑坡体物质组成分类等。不管何种分类形式，一个典型滑坡往往具有标志性的滑动面，有些滑坡虽然看不出明显的滑动面，但根据开裂裂缝也能判断出滑动面位置。为分析方便，建立如图1所示滑坡分析模型，各部分名称此处不做叙述。

借鉴土力学中关于土体作圆弧滑动方面的知识，我们将滑坡失稳原因归结为下滑力矩大于阻滑力矩，从而形成力矩形式下的滑坡稳定性系数表达式，如公式（1），这也是各种规范中给出的处理思路。

式中，MR为滑坡体沿滑动面的下滑力矩 （kN·m）；Ms为由滑动面的内聚力和摩擦力形成的阻滑力矩（kN·m）。

当由式（1）计算得到的 Fs＞1 时，滑坡处于稳定状态；当 Fs＜1 时，滑坡处于非稳定状态；当Fs=1时，滑坡处于极限平衡状态。当然，这是在未考虑安全储备的情况下给出的判定方式，在需要考虑安全储备的情况下又另当别论。

虽然上述处理方法是经典的，也是规范推荐的，但是很多时候计算的结果并不十分让人满意，当然很大一部分原因源自实际工程的复杂性，毕竟现有理论研究的问题都趋于理想化，但是还有一部分原因来自于我们并没有完全掌握滑坡发生滑动的实质，即断裂的问题。滑坡发生滑动本质上还是滑动面上未贯通部分发生断裂、扩展，并最终导致整个滑动面的贯通，这显然是一个典型的断裂力学问题，针对滑坡分析模型，从中提炼相应的断裂分析模型，对于滑坡失稳机制的研究无疑是积极的。

2 滑坡失稳的断裂力学分析

我们认为未发生滑动的滑坡体滑动面上存在所谓的贯通段和未贯通段，表现在图1上即为图2所示。

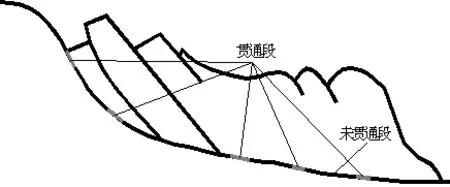
图2 含贯通段和非贯通段的典型滑坡断面图

从力学角度来看，此类典型滑坡滑动面土体单元皆处于压（拉）剪应力状态，因此可以采用同一断裂模型代替分析。我们在滑坡滑动面上包含贯通段一定范围取单元，建立断裂分析模型，如图3所示，（a）类模型是在滑坡顶部滑动面取单元构建的，（b）类模型是在滑坡中部滑动面取单元构建的，下面分别针对这两类断裂模型进行求解。

图3 滑坡滑面处断裂分析模型

（1）滑坡顶部滑面处断裂分析模型裂纹尖端应力强度因子求解滑坡顶部滑面处断裂分析模型中的裂纹显然属于边裂纹的情形，考虑到实际工程中，裂纹的长度相对于滑坡的宽度可以忽略不计这一事实，我们将断裂模型的边界视为无限边界，查阅《应力强度因子手册》，此模型可按下图方式进行等效。

图4 滑坡顶部滑面处断裂分析模型等效处理

等号右边第一个模型中的σ和τ分别按（3）、（4）式变化

等号右边第二个模型中的σ和τ则分别按（5）、（6）式变化

针对等号右边第一个模型，查阅《应力强度因子手册》有

针对等号右边第二个模型，查阅《应力强度因子手册》有

因此滑坡顶部滑面处断裂分析模型裂纹尖端应力强度因子计算公式如下：

至此，滑坡顶部滑面处断裂分析模型裂纹尖端Ⅰ型、Ⅱ型应力强度因子皆求解完毕。

（2）滑坡中部滑面处断裂分析模型裂纹尖端应力强度因子求解

滑坡中部滑面处断裂分析模型中的裂纹可视为无限边界板所含的中心裂纹，针对此断裂模型，《应力强度因子手册》中载有现成的计算方法，如以下两式。

至此，滑坡中部滑面处断裂分析模型裂纹尖端Ⅰ型、Ⅱ型应力强度因子也求解完毕。

（3）相当应力强度因子求解

按复合型断裂问题相关理论，决定复合型裂纹是否扩展的参考量是裂纹尖端相当应力强度因子，它的计算可按式（15）。

式中，KⅠ、KⅡ分别为上面求得的Ⅰ型、Ⅱ型应力强度因子；θ0为裂纹扩展的断裂角（°），计算方法可参考相关书籍，此处不作赘述。

按（11）～（14）式可计算两类模型裂纹尖端Ⅰ型、Ⅱ型应力强度因子，结合式（15），可进一步求得对应的相当应力强度因子，在获取滑面处岩土体的断裂韧性之后可做断裂稳定性判断，以此揭示滑坡失稳的断裂机制。

3 结语

本文在总结前人研究成果的基础上，深入分析了滑坡失稳的断裂机制，但其中也存在几点缺陷，总结如下：

（1）由于滑坡滑面处于岩土体内部，我们无法预知滑面处的贯通段和未贯通段的具体位置，这给理论分析带来了极大的障碍，当然现在有许多探伤设备，但造价都不低，精确度也有待提高，所以这个问题亟待解决。

（2）在进行断裂稳定性判断的时候需要提前知道滑面处岩土体的断裂韧性，这一点在实际工程中是较难得到的参数，况且在取岩土样本的时候带来的扰动有时影响很大。

（3）查阅《应力强度因子手册》得到的计算公式部分带有近似性。

［1］DB50/5029-2004重庆市地方标准：地质灾害防治工程设计规范[S].重庆,2004.

［2］周福川,王小委.滑坡治理中的土质锚杆位移研究[J].科学技术与工程,2014,14(15)：295-299.

［3］朗惠芳,代彤.基于裂纹线场分析法的滑坡失稳机理分析[J].山西建筑,2009,35(17)：105-106.

［4］赵队家,毛新虎,胡夏嵩.某滑坡的变形模式与形成机制研究[J].青海大学学报：自然科学版,2003,21(6)：29-33.