数学建模融入运筹学教学的探索与实践

殷月竹

(安徽理工大学理学院数学系，安徽 淮南232001)

1 运筹学的特点

运筹学是一种研究在给定的物质条件（人力、物力、财力)下，运用科学的方法主要是数学方法，进行数量分析、统筹兼顾，最经济、最有效地使用人力、物力、财力，以期达到最佳效果的科学方法。运筹学课程具有如下特点：

1.1 应用性

运筹学就是从实践和应用中发展而来的，因此它从一开始就有着强烈的应用性。目前，除了传统的应用领域外，运筹学已广泛应用于航天、通信、自动化等高新技术领域。

1.2 综合性

运筹学是一种综合应用数学、计算机科学、管理学、社会学、经济学等学科的科学方法，这些学科相互渗透、交叉，综合运用。

1.3 最优性

运筹学强调最优性，既在空间上寻求整体最优，又在时间上寻求全过程最优。

2 数学建模意义

2.1 数学建模能够大大提高学生学习数学的兴趣

我们知道，大学数学课程让不少大学生感到比较难学，甚至害怕。而在传统的数学教学中往往重理论、轻实践，使学生对数学的应用性认识不足，从而使学生产生厌学情绪，大大降低了学习数学的兴趣。而数学建模的题目多数来源于生活中的一些热门实际问题，充分体现出数学的应用性，学生通过参与数学建模活动，能够充分体会到利用数学工具解决实际问题的快乐，从而激发学生学习数学的兴趣。

2.2 数学建模能够提升学生的思维能力、创新能力以及表达能力

由于实际问题各种各样、千变万化，故数学建模题目大都灵活性很强，事先并没有标准的答案。学生针对同一问题可以从不同的角度、运用不同的方法去解决，但只要所建立的数学模型合理可行、具有创新性，并能用文字清晰地表达出来即可。因此，数学建模加强了学生的思维能力、创新能力和表达能力。

2.3 数学建模能够加强学生综合运用知识解决实际问题的能力

由于建模问题主要来源于各个领域的实际问题，故解决它需综合运用相关各个领域的知识，但任何学生又不可能全面掌握各个领域的专业知识，因而学生在建模过程中就需要查阅大量的文献资料，并有针对性地汲取和利用，因此，学生通过数学建模，可以加强综合运用所学知识解决实际问题的能力。

3 数学建模在运筹学中的教学案例

综合上述运筹学的特点和数学建模的意义来看，运筹学应该是与数学建模结合的最为密切的课程之一，因此，在运筹学的教学上，一定要体现数学建模的思想，并密切结合数学建模的案例。

例1 “田忌赛马”问题

在上运筹学的第一次课时，我就引入“田忌赛马”的故事：田忌与齐王赛马，两人各有上、中、下3个等次的马，两人规定三局两胜。若按同等次比，齐王的马均比田忌的马略胜一筹，田忌肯定会输；于是田忌想出一个策略：用他的一等马对齐王的中等马，中等马对齐王的下等马，下等马对齐王的上等马，结果田忌两胜一负，终获胜利。

分析：这是我国著名的一个历史故事，田忌充分利用现有的条件，统筹考虑，取得了最佳比赛成绩。这个故事的引入，不仅充分体现出了运筹学的优化思想，而且避免了直接给出运筹学的定义和研究对象的枯燥乏味，同时大大激发了学生的学习兴趣。

例2 “学生选课问题”

某高校规定，应用数学专业的学生必须至少学习过3门数学课程、2门运筹学课程和2门计算机课程且考试或考查合格才能毕业.这些课程的编号、学分、所属类别和选课要求见表1.如果某生既希望所学课程的数量少，又希望所获学分高，那么他该如何选课呢？

表1

分析：这是一个学生非常关心的学习上的实际问题，属分配优化问题，可建立一个0—1规划的数学模型，由此可引出整数规划及0一l规划问题的求解方法.又可引出多目标规划问题。

例3 “服装评判”问题

设U={款式花色，耐穿程度，价格费用}，V={很欢迎，比较欢迎，不太欢迎，不欢迎}，现有一服装，其相关信息见下表2，请对其中单个元素进行评价。

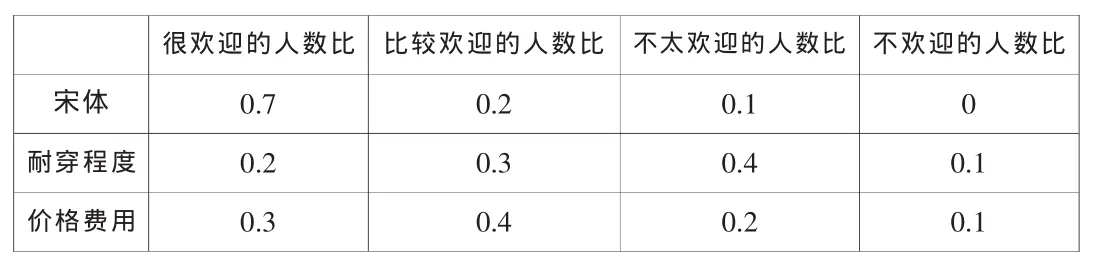
表2

分析：这是一个非常贴近学生日常生活的实际问题。我们可以利用模糊综合评判法，将上述所有单因素组成一评判矩阵：

由于每个人的性别、爱好、经济状况等的不同，对服装的三要素U所给予的权数也不同。若某班学生给出的权数为B=（0.5,0.3,0.2），采用模糊综合评判模型，可得该班学生对这种服装的综合评判为：

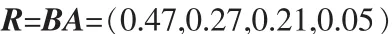
它表示的意思是“很欢迎”的程度为0.47，“比较欢迎”的程度为0.27，“不太欢迎”的程度为0.21，“不欢迎”的程度为0.05.按最大隶属原则，结论是该服装很受欢迎。

4 结束语

总之，在教学中，我适时地结合学生的日常实际问题做案例分析，并进行数学建模，发现对学生的益处很多，比如让学生真正“学有所用”，很大程度地提高了学习兴趣，还促进了学生对数学软件的学习和利用，同时也有利于学生成长为21世纪所需要的具有科学管理、运筹决策能力的复合型人才。

［1］宇世航,张水胜,张良勇.数学建模思想在“运筹学”教学中的运用[J].高师理科学刊,2009,29(6)：89-91.

［2］乐励华,戴立辉,刘龙章.数学建模教学模式的研究与实践[J].工科数学,2002,18(6)：9-12.

［3］姚香娟,段滋明,王萃琦.如何提高学生学习运筹学课程的兴趣[J].学园,2014(12)：59-59.

［4］唐海军,李玲,罗方芫.基于数学教学优化的建模课分析[J].成都师范学院学报,2013,29(11)：113-115.

［5］林军，陈翰林.数学建模教程[M].科学出版社,2011：180-182.