应用矢量的非常规分解简捷解题

白云朋

(安徽省合肥市第九中学，安徽合肥 230001)

解决物理问题，既要能熟练应用常规方法，又要能突破常规灵活求解.如分解一个矢量时，没有必要一定采用常规的分解方法(如分解力时常用的正交分解法)，也可以采用非常规的分解方法.因为没有特殊限制的话，一个矢量可以分解为无数对大小、方向不同的分矢量，这些分矢量共同作用的效果，都与那一个矢量单独作用的效果相同，所以，分解矢量完全可以打破常规采用其他的方法.如对中学物理中出现的小船渡河、力的分解、平抛运动、斜上抛运动等问题来说，如果善于打破常规采用非常规分解方法，会有简捷快速的效果，也会对活学物理有一定的启发.本文对所举例题的常规分解方法将不做赘述.

1 小船过河问题的非常规分解

处理小船渡河问题，如果应用分解速度的方法，常规方法是将船速平行河岸和垂直河岸分解，少有采用同时分解船速和水速的方法.下面的例题就采用这种非常规分解方法.

例1.一艘小船在静水中的速度v=3 m/s，河水沿平直的河岸流动，假设各处的水速都相同，均为u=5 m/s.一船夫要驾此船渡河并且要求渡河时通过的距离最短，那么船夫应该选择向哪个方向划船?

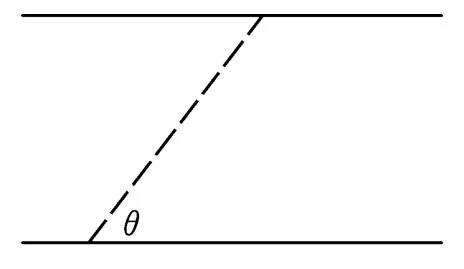
图1

图2

2 力的非常规分解

分解力的常规方法是正交分解，即将力向两个互相垂直的方向分解.如果具体问题能具体分析，有时用非正交分解反而简捷.

例2.一倾角为θ的斜劈放在水平地面上，一物体沿斜劈匀速下滑.现给物体施加如图3所示的力F，F与竖直方向的夹角为β，斜劈仍静止，物体加速下滑，试确定此时地面对斜劈的静摩擦力的大小和方向.

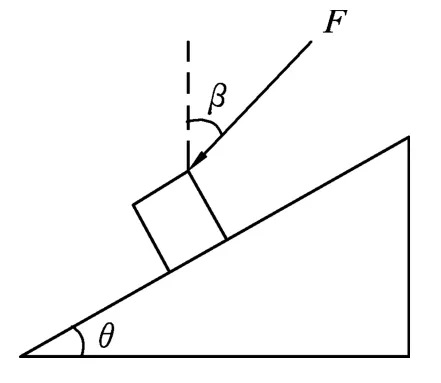
图3

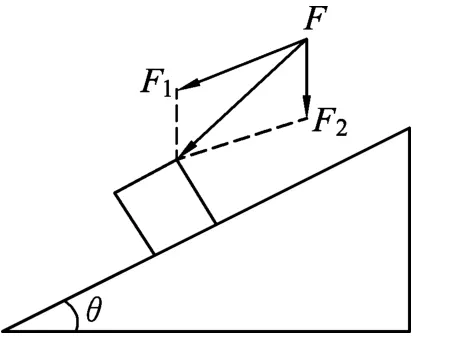
图4

解析:如图4，将力F分解为平行斜面的分力F1和竖直向下的分力F2，有如下分析:

(1)没有施加力F时，物体沿斜面匀速下滑，因此物体受到的斜劈对它的支持力FN和摩擦力Ff的合力大小等于物体的重力mg，方向竖直向上(如图5)，且由mgsinθ=umgcosθ能推导出物体、斜劈之间的动摩擦因数μ=tanθ.根据牛顿第三定律，斜劈受到的物体对它的两个反作用力FN'、Ff'的合力的方向竖直向下(如图6)，斜劈水平方向不受力，所以地面对静止的斜劈没有静摩擦力.

图5

图6

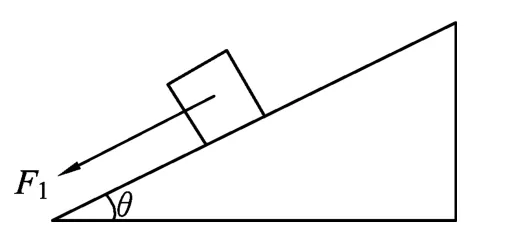
图7

(2)如果只施加力F1(如图7)，由于F1平行斜劈，F1不会改变斜劈对物体的支持力FN和摩擦力Ff的大小和方向，仍有FN=mgcosθ和Ff=mgsinθ，改变不了斜劈受到的反作用力FN'、Ff'，FN'与Ff'的合力的方向仍竖直向下，斜劈水平方向仍然不受力，所以单独施加力F1时，地面对斜劈没有静摩擦力.

(3)如果只施加力F2(如图8)，等效于物体的重力变为mg+F2，如图 9.由于 μ =tanθ，mg+F2(mg+F2)sinθ=μ(mg+F2)cosθ成立，物体仍做匀速运动，斜劈对它的支持力和摩擦力的合力的方向还是竖直向上，它对斜劈的反作用力的合力的方向仍竖直向下，斜劈水平方向还是不受力，所以只施加力F2时，地面对斜劈没有静摩擦力.

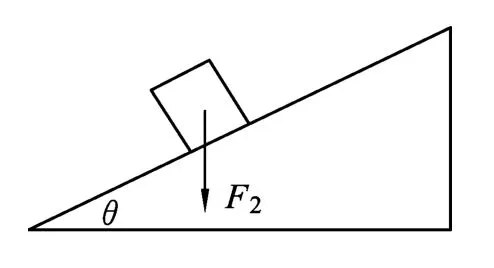
图8

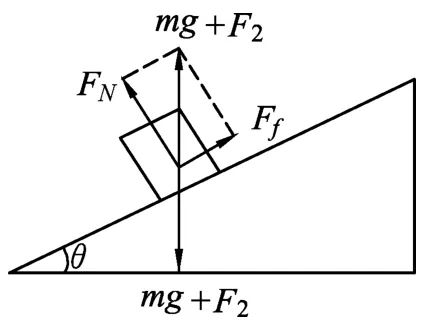
图9

综上所述，由于力F的作用效果与分力F1、F2共同作用的效果相同，故施加如图3所示的力F后，地面对斜劈没有静摩擦力.

3 平抛运动的非常规分解

平抛运动的常规分解方法是将其分解为水平方向的匀速直线运动和竖直方向的自由落体运动.但也不必过分拘泥常规，下面的例题采用另一种分解方法从而简捷求解.

例3.如图10所示，在倾角为θ的一无限长斜面上某点以初速度v0水平抛出一弹性小球，一段时间后小球落到斜面上的另一点，与斜面弹性碰撞后又落到斜面上的另外一点……，这种碰撞反复进行，不计碰撞过程所用的时间，忽略空气阻力.试分析:(1)小球相邻落点之间的距离成等差数列吗?(2)相邻落点之间轨迹的顶点在不在同一条直线上?(3)这些顶点之间的距离成等差数列吗?

图10

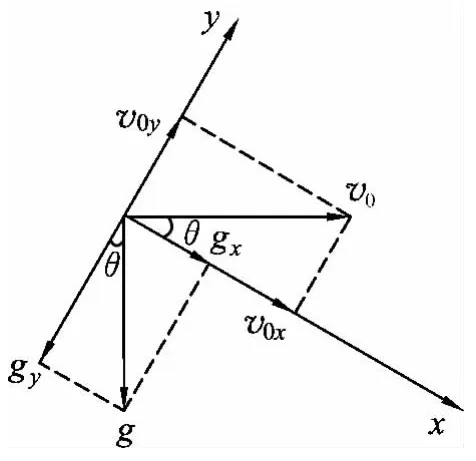
图11

解析:将小球的运动分解为沿斜面方向(x方向)和垂直斜面方向(y方向)的分运动，如图11所示.在x方向上小球做初速为v0x=v0cosθ、加速度为gx=gsinθ的匀加速直线运动.在y方向小球做初速为v0y=v0sinθ、加速度为gy=gcosθ的类竖直上抛运动.

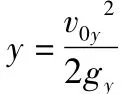
4 斜上抛运动的非常规分解

斜上抛运动的常规分解方法是分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动.斜上抛运动也可以采用另一种分解方法:将其分解为初速度v0方向上的匀速直线运动(在此方向上物体不受力)和竖直方向上的自由落体运动(在此方向上物体受到重力但无初速度)，如图12所示.采用这种方法可以简捷处理用常规方法需复杂求解的问题.

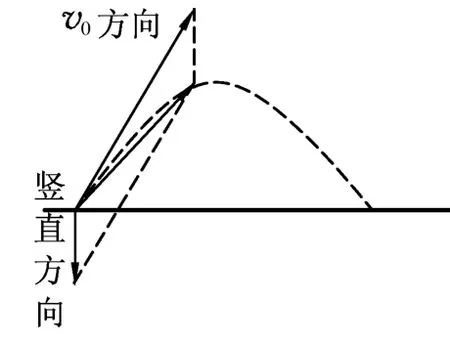
图12

图14

图15

例5.如图15所示，一足够长的斜面倾角为θ，在斜面上的某一点以相对于斜面的仰角β发射一发炮弹，忽略空气阻力，试求炮弹在斜面上射程最大时的仰角β及最大射程sm．