ANSYS14.0重分网格技术在方形液压密封圈大变形优化分析中的应用

王素粉 秦 冲

（三门峡职业技术学院，河南 三门峡472000）

0 引言

方形液压橡胶密封圈在械及液压设备应用当中具有很重要的作用，直接影响液压系统的密封效果及传动的稳定性，而在进行液压密封圈设计的时候主要利用到固体力学、摩擦学、高分子材料学等多方面的知识，这对于液压密封圈的精确研究也造成了一定的难度，特别是液压橡胶密封圈的密封机理和失效机理。所以，在现有的条件下，通常依靠经验进行液压密封圈的设计。而方形液压密封圈在密封槽内的应变应力分布是影响其密封性能的重要参数，会因为摩擦力的存在而发生扭转变形等，所以要对其进行有限元分析，然而，在利用有限元进行分析的时候，密封圈发生大变形的过程中网格会发生畸变，这种畸变就造成了造成有限元分析计算结果失败，造成方形密封圈非线性分析不收敛。本文运用ANSYS14.0这种强大软件对计算失败的方形液压密封圈进行了重分网格划分，通过将网格重分前旧网格结果映射到新网格结果进行重新求解，得出了其完整的变形结果，解决了材料因网格畸变引起的大变形非线性分析求解不收敛的问题，为方形液压密封件的密封计算及密封性能研究提供了一定的理论基础，对其他大变形材料的分析也提供了重要的研究方法。

1 模型的建立

1.1 Mooney－Rivlin材料模型建立

本文中的圆形刚性轴和刚性匹配件假定为刚体，而方形液压密封圈采用的是橡胶材料，此材料为超弹材料，平面单元选择的是PLANE182，假定刚性圆柱与密封圈之间是无摩擦，建立模型，密封圈的弹性模量为14.04MP，泊松比为0.4999，方形密封圈的超弹本构关系采用两参数Mooney－Rivlin材料模型，Mooney－Rivlin材料模型是广义Rivlin模型的一个特殊情况，即为金属材料当中的应力应变关系，用多项式表达的超弹性模型为应变能势函数，如式1所示：

Cpq为和材料畸变响应有关的材料常数，而Dm是与体积响应有关的材料常数，对于可压缩的Mooney－Rivlin材料，N＝1，C01＝C2，C11＝0，C10＝C1，M＝1，所以我们可以得到：

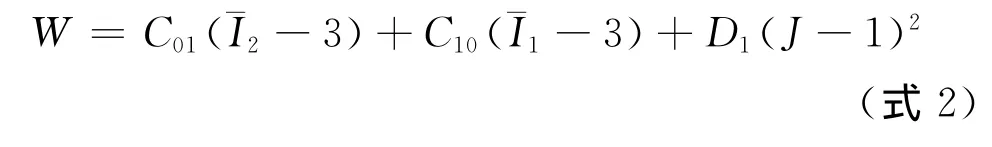
式中：C10和C01为材料常数，均为正定常数，对于大多数橡胶而言，在应变150%以内，都可以得到合理的近似分别为第1、第2Green应变不变量，，d为材料的不可压缩参数，一般为d＝0.0001mm。

其中：

在进行材料模型定义时，只需要输入C10、C01和d三个参数即可。而C10、C01参数的确定又和材料的弹性模量有关，通过分析和计算三个参数值分别为、C10＝55 MP C01＝－32.5 MP和d＝0.0001mm。

1.2 几何尺寸模型

本文研究的是一个密封圈的大变形情况，该几何模型可以把密封圈装配体看成是由方形密封圈、圆形刚性轴和刚性匹配件组成的模型，主要尺寸如图1所示，图中几何尺寸为：L＝20mm，H＝60 mm，L1＝80mm，D＝18mm，H1＝0.05 D.根据图1所示，依次建立方形密封圈模型、圆形刚性轴模型、刚性匹配件模型。

2 网格划分及求解分析

2.1 初次网格划分

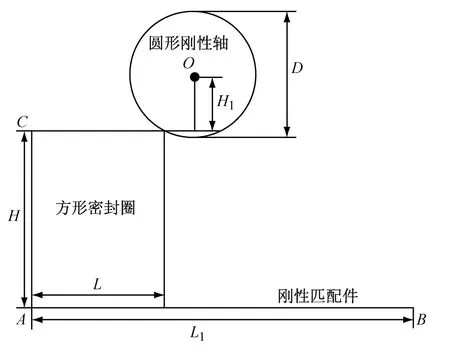
图1 密封圈装配体系统简图Fig.1 the diagram of seal assembly system

对建立好的有限元模型进行网格划分，首先进行总体网格控制设置，把L分成9等份，也就是单元尺寸输入L/9，然后利用Mesh命令进行密封圈网格划分，网格划分完成后，进行接触对定义，此密封圈系统主要有两个接触对，一个是圆形刚性轴与方形密封圈接触对，为刚—柔接触对，其接触面为与圆形刚性轴接触的两条线，另外一个接触对是刚性匹配件AB与方形密封圈刚—柔接触对，这两个接触对在进行创建的时候均假设摩擦因数为0。网格划分结果如图2所示。

图2 密封系统有限元网格划分Fig.2 the finite element meshing of sealing system

2.2 施加约束求解

对于划分好的网格进行约束施加约束，本文通过控制刚性移动件来施加约束，对于方形密封圈而言，其约束为AC边的横向约束，即约束X方向的位移，选择约束类型为UX；对于刚性匹配件AB为ALL DOF，而对于圆形刚性轴约束为UX和ROTZ，施加载荷选择的是刚性匹配件的控制点，约束自由度类型为UY，其位移值为－15。其约束结果如图2所示。根据要求设置的求解类型为时间—子步类型，计算时间为1，子步数量为10，最大子步为100，在和加载方式为斜坡加载。待重启动设置后进行求解，求解运行状态显示曲线如图3所示，从图3中可以看出，求解过程在时间为0.427051s的时候终止，其原因是如图5所示网格发生扭曲造成的分析运行终止，造成了非线性求解不收敛，所以，必须进行网格重分。

图3 网格重分前密封圈静态分析求解状态图Fig.3 the static analysis solving state diagram of sealing ring before mesh subdivision

图4 重分网格前计算列表Fig.4 Calculate list before mesh subdivision

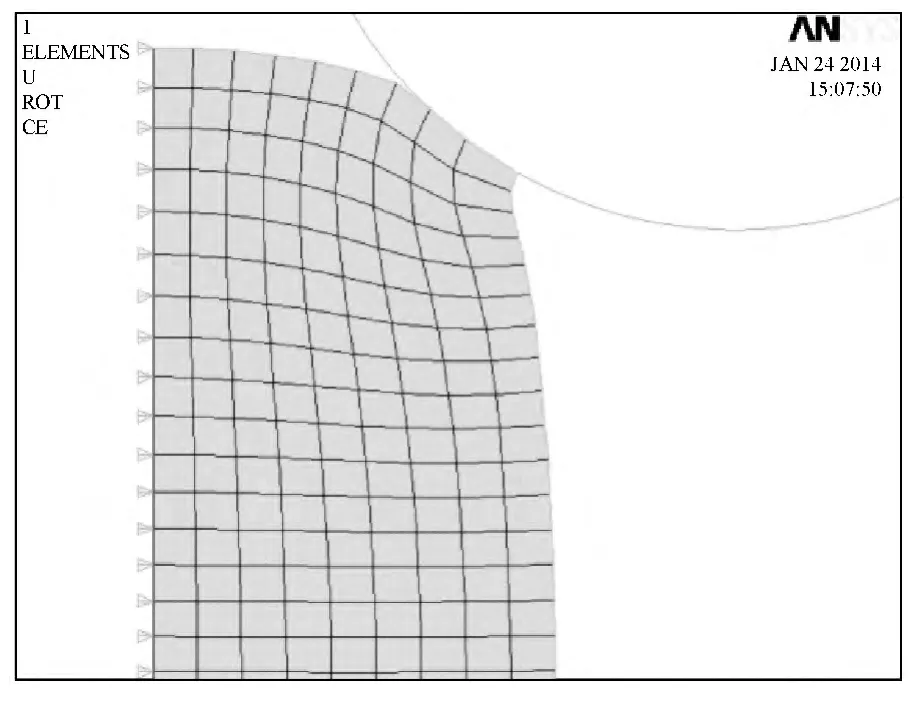
图5 第8子步重分网格前网格变形图Fig.5 The deformation figure of the 8sub－step before the mesh subdivision

2.3 重分网格及处理

由于在未进行网格重分时求解终止，造成了非线性求解出现不收敛情况，那么势必会对求解过程造成了影响，所以要进行网格重分，从图4可以看出，运行结果只有11步，从第11步可以看出不收敛，所以防止再次出现运行结果不收敛情况，本文从第8个子步开始重分网格，首先进行选择网格重分单元，如图6所示，形成的网格重分的面区域如图7所示。

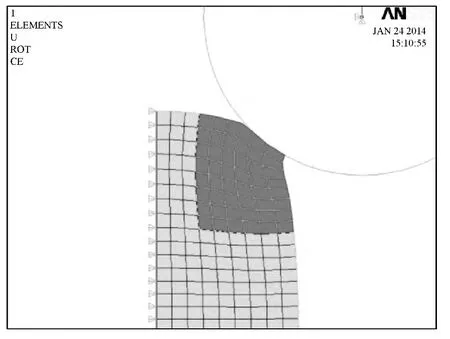
图6 选择重分网格单元Fig.6 the grid cell selection of mesh subdivision

图7 重分网格的面区域Fig.7 the surface area of mesh subdivision

2.4 网格重分后静力学分析

重分网格后将旧网格结果映射到新网格，最大迭代子步数为50，在进行网格充分后进入求解设置重启动，再次进行求解运算。运行状态如图9所示，从图7可以看出，此状态与所设置的运行时间Time＝1相吻合，也就是说在运行过程中未出现运行终止情况，从而可以判断此非线性求解过程是收敛的。图8为第8子步重分网格后运行结果，从图10可以看出，子步为第8步之前都是保存在rst文件，而从第9步开始后面的都存在rs01文件，说明从第9步开始后面都属于重分区域。

图8 第8子步重分网格后的网格变形图Fig.8 the mesh mesh deformation figure of 8substeps after mesh subdivision

图9 网格重分后密封圈静态分析求解状态图Fig.9 the solving state diagram of static analysis of the seal after mesh subdivision

图10 重分网格后计算列表Fig.10 Calculate list after mesh subdivision

图11是进行网格重分后的密封圈的网格变形云图，其最大变形量为8.812mm，图12是进行网格重分后的密封圈重分网格后的等效应力云图，从图中可以看出其最大应力为507.846MP，图13为进行网格重分后的密封圈重分网格后的接触压力云图，从图中可以看出其最大压力为456.517MP，图14为进行网格重分后的密封圈重分网格后的接间隙云图，从图中可以看出其最大间隙为－3.88061mm。

图11 重分网格后变形云图Fig.11 the deformation nephogram after mesh subdivision

图12 重分网格后的等效应力云图Fig.12 the equivalent stress nephogram after mesh subdivision

3 小结

本文首先利用ANSYS14.0建立了方形液压密封圈橡胶材料的几何模型及两参数Mooney－Rivlin材料模型，之后对其进行了初次网格划分及重分网格划分与求解，得出了液压密封圈的网格重分前后的变形情况，通过对比可以发现，对于方形液压密封圈进行有限元分析时会因发生网格畸变而终止，造成求解结果不收敛，而进行网格重分的子步进行重新求解后，所变形结果是完整的且收敛的，得出密封圈的变形云图、等效应力云图、接触压力云图、间隙云图等，从而可以得出一些重要的分析参数，这一方法的研究解决了材料因网格畸变引起的大变形非线性分析求解不收敛的问题，为橡胶密封件的密封计算及密封性能研究提供了一定的理论基础，对其他大变形材料的分析也提供了重要的研究方法。

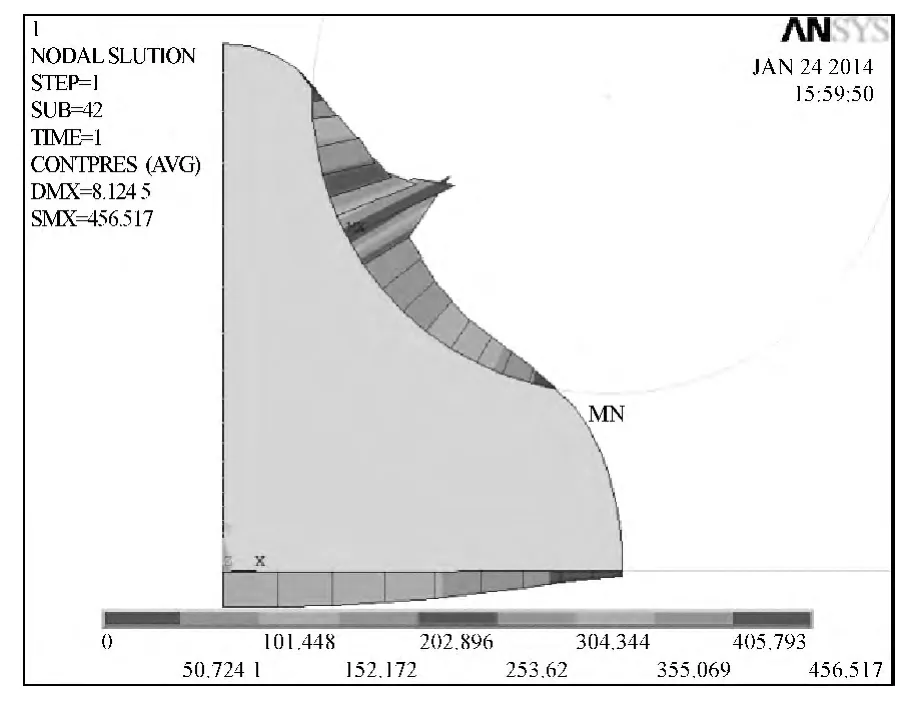
图13 重分网格后的接触压力云图Fig.13 the contact stress nephogram after mesh subdivision

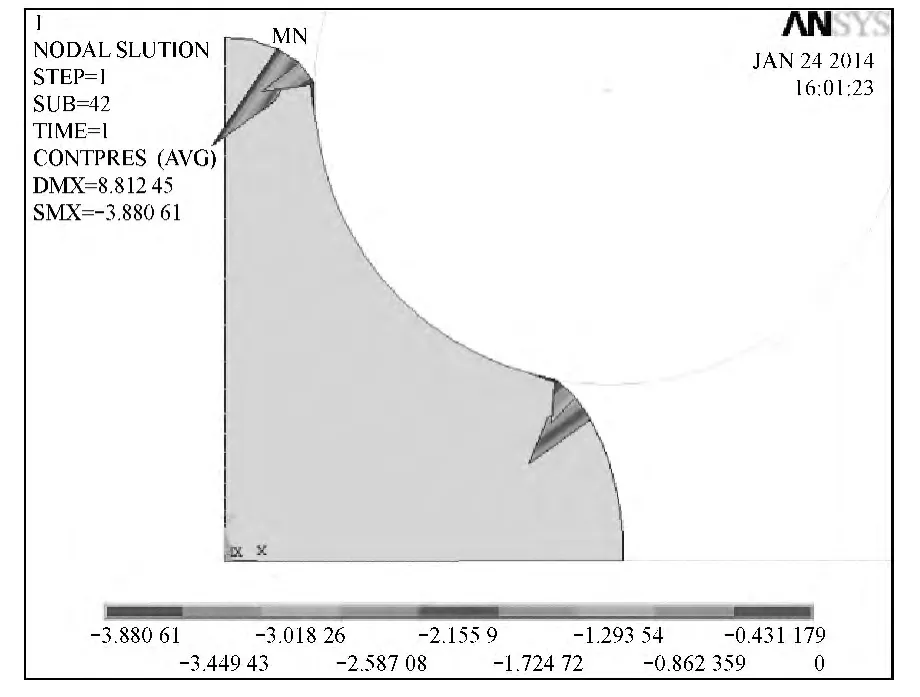
图14 重分网格后的间隙云图Fig.14 the clearance nephogram after mesh subdivision

［1］ 胡旭林基于 Workbench的O形圈多参数非线性优化［J］.煤矿机械2013（5）.

［2］ 谭 晶等.矩形橡胶密封圈的有限元分析［J］.润滑与密封2007（2）.

［3］ 张国智.基于网格重划分的冲孔剪切带的模拟方法研究［J］.机械设计与制造2010（4）.

［4］ 王 伟等.橡胶Mooney—Rivlin模型中材料常数的确定［J］.特种橡胶制品2004（8）.

［5］ 张洪才.ANSYS14.0工程实例解析与常见问题解答［M］.机械工业出版社2013（4）（248－260）.