基于遗传算法的瞬变电磁法线圈阵列优化设计

杨龙成, 陆继庆, 刘冀成, 张 帅

(成都信息工程学院电子工程学院,四川成都610225)

0 引言

瞬变电磁法(Transient Electromagnetic Method,简称TEM)[1-3]是一种常用的地下物质探测方法,广泛应用在石油管道检测与地下固体废物与污染物探测,以及考古、土壤评价和城市管线探测等方面。但是由于模型的设计局限,遇到障碍物时严重影响了探测精度,传统的圆形线圈和“8”字形线圈[4-7]聚焦性较差,聚焦时会影响大面积非目标区域;目前在瞬变电磁检测技术中,对线圈阵列的磁聚焦技术研究却相对较少,而且载流线圈的空间磁场解析表达式也较为复杂[8-9]。这些成为阻碍其发展的重要原因。

文中从单个三角形模型出发,计算其空间磁场分布,参考了在经颅磁刺激方面磁聚焦的研究成果,设计了“8”字形等边三角形构成的线框阵列,研究表明经遗传算法的优化可以改善磁聚焦特性,有效地加强目标区域的磁场强度,同时又较好地抑制非目标区域的电磁场强度[10],从而提高激励线圈阵列的磁聚焦特性,达到改善探测精度的目的。对磁聚焦的发射回线模型结构的研究具有实用价值与指导意义。

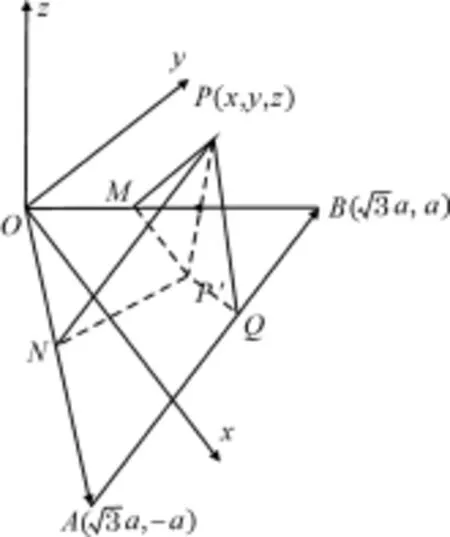
图1 三角形空间B场分布

1 三角形空间磁场

1.1 三角形空间磁场计算

通过对已有文献的总结发现,对圆形载流线圈[11-13]的研究明显多于对三角形或正三角形载流线圈[14]的研究,但是研究表明三角形载流回线的磁场分布在聚焦性方面比圆形线圈略有改善。因此,以三角形为基础,对其空间磁场分布进行了详细的计算。如图1,正三角形载流线框由3段载流直导线组成,根据载流直导线在空间的磁场分布和磁场叠加原理,对其进行分段计算、叠加,最终得出正三角形载流线圈在场点P(x,y,z)产生的磁感应强度B的3个分量分别为:

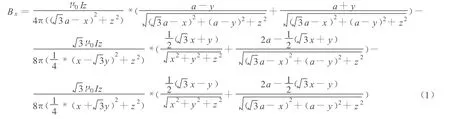
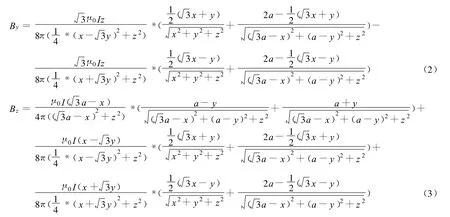
1.2 三角形空间磁场分布

线框的空间磁场计算区域为4m×4m×4m。线框匝数为1匝,通入1A电流。为了避免或减小截断误差,对磁场强度进行归一化处理,这样不仅可保证参与计算的量数值相差不大,而且归一化过程中可能得到相似参数。X代表在x轴上的分部间隔,Y代表在y轴上的分部间隔,｜B｜/｜Bmax｜代表在z轴方向上的B场归一化值。图2(a)是磁场二维等高线分布图,图2(b)是归一化B场值分布图。

图2 单个线圈模型生成的B场分布

由图2知:在Z=112.8cm的观测平面,单个线框模型的87.5%及以上的磁场能量集中在半径为0.315m区域内,目标区域内的归一化极大值1.0与极小值2.41×10-8之比达到7个数量级,磁场分布面积为1.12m×1.12m,磁场能量在空间以环形分布向外辐射,造成地下检测的覆盖面积过大,分布梯度小,在线框几何中心处磁场强度相对较弱,聚焦性能不是很好,易受外部干扰,对小目标物质检测准确度与精度不高。

2 线圈阵列的设计

根据磁聚焦技术在经颅磁刺激等方面的研究成果,为了对三角形磁场聚焦性进行优化,设计了“8”字形等边三角形发射回线模型。针对三角形形状的特殊性,其“8”字形模型有两种情况,如图3所示。根据初步的计算结果与CST(电磁工作室)的模型仿真结果表明,其中只有一种组合具有较好的聚焦性,在改变其重叠区域以及三角形线框的边长时发现,图3(a)所示组合的磁场分布改变明显,因此对其进行优化设计,最终得到一种更好的磁聚焦模型。

3 线圈阵列的优化

由(1)、(2)、(3)式可知,影响某一点磁场感应强度的只有通入线框的电流和线框的边长,考虑到线框阵列模型,那么其重叠区域的长度也是至关重要的一个参数。因此利用遗传算法对线框的参数电流、线框边长和重叠区域进行优化,达到磁聚焦优化的目的。

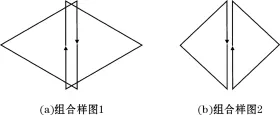
图3 等边三角形线圈阵列

3.1 遗传算法

遗传算法(Genetic Algorithms,简称GA)[5]是随机自适应全局搜索的优化算法,算法模仿生物遗传与进化的特点,将需求解问题转化为目标函数的极值问题。算法一方面依据进化理论鼓励更优秀的解结构;另一方面在多次的迭代中依据遗传变异原理,保持种群中优秀的个体,同时继续寻找更优的解结构。利用遗传算法求解问题时,须首先对求解问题的参数空间进行编码,用随机选择作为工具,依据进化与变异理论,引导算法的搜索向更有效地方向发展。

3.2 参数选择

个体编码:将电流i、线框边长a和重叠区域d作为优化参数,每个参数选用二进制编码,电流取值为-1、0、1中的一个,线框边长a步长为0.05m,取值区间为[0.1,1],重叠部分d∈[0,0.8],步长0.01m。

种群规模:根据适应度函数值选取的一组解N=200。

选择自适应交叉和变异[15]方法。

最佳个体保留:选取5%*N个父代种群中适应度值最高的个体,不经过任何的操作直接复制到子代种群中,保持种群中优秀的个体,加快算法的收敛速度。

3.3 适应度函数

适应度函数(fitness function)反应算法中每一个个体的质量,是遗传算法中选择进化的依据,它的选取直接影响了遗传算法的性能、收敛速度以及算法是否能找到最优解。线圈阵列的目的是约束空间磁场分布,要求优化算法的适应度函数能映射出线圈阵列在特定深的较小区域内产生较大的磁场强度。适应度函数为:

式(4)中:S0.875表示大于最大场强值的0.875倍区域所占的面积,S表示整个计算区域的面积。Bcen表示从CST输出中计算区域中心的磁场,Bmax为计算区域的最大磁场值。将计算平面上的平均场强度S0.875与整个平面的平均磁场强度S相除,通过指数函数对其计算处理求出最小值来改善聚焦的性能,保证提高探测的精度,再与Bcen/Bmax相乘求解磁场强度最大值,来提高探测的刺激力度与强度。由此,适应度函数转化为数学模型中的求解fitness最大值。

3.4 优化算法的流程

优化算法的流程如图4所示。

4 优化结果与讨论

4.1 优化结果

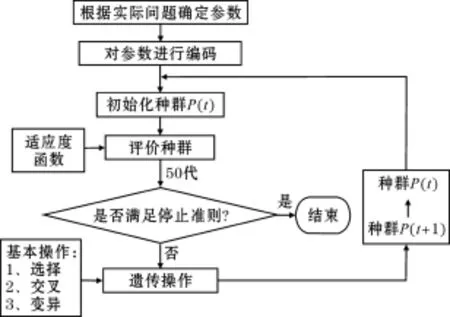
图4 优化算法流程图

通过分析,线圈阵列模型的参数范围与经GA优化后的参数取值如表1所示,经过实物加工和测试,与传统的TEM系统相比,磁聚焦TEM系统不仅缩小每个检测点的覆盖长度,而且提高了埋地1.3m深处并行或重叠埋地金属物质或石油管道等的分辨率与检测准确度。

表1 发射线圈阵列的参数

整个优化计算中,线框阵列的空间磁场计算区域也为4m×4m×4m,两线框所在平面的垂直距离为3cm。每个子线圈匝数为1匝,通入1A电流。采用归一化处理得到如下的仿真效果图,图5(a)是磁场二维等高线分布图,图5(b)是归一化B场值分布图。

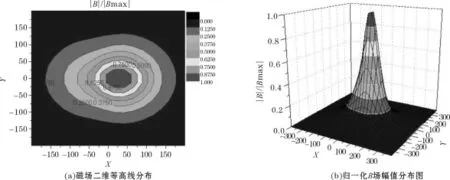
图5 优化线圈模型生成的B场分布

4.2 讨论

综上,同等深度Z=112.8cm,优化后得到的正三角形阵列的磁场分布面积为0.81m×0.81m,归一化极大值1.0与极小值4.1528×10-9之比达到8个数量级,阵列模型中87.5%及以上的磁场能量集中在半径为0.113m区域内,相比于三角形线框模型,阵列模型的几何中心处磁场强度最大,能量集中区域最小,分布梯度最大,聚焦性能明显提高,同时又较好地抑制了非目标区域的磁场强度,较容易对小目标物质进行检测,提高了检测的精度与准确度,从而很好地实现了磁聚焦。

5 结束语

通过叠加原理对单个三角形线框空间磁场的计算,设计了等边三角形线框阵列模型,经过遗传算法对其参数的优化,新模型仿真结果表明:线圈阵列激励磁感应强度在计算平面上的分布梯度较大,且绝大部分磁场能量集中在较小范围内,很大程度提高了磁场聚焦功能。此模型结构简单,聚焦效果很好,可有效提高TEM技术对埋地金属物质与金属管道蚀失量[16]等的检测与分辨的准确性,可进一步优化磁聚焦的激励线圈阵列,扩大磁聚焦的应用范围,对线圈阵列在磁聚焦中的运用起到了指导研究作用。

[1] 朴化荣.电磁测深法原理[M].北京:地质出版社,1990.

[2] 考夫曼A A,凯勒G V.王建谋译.频率域和时间域和时间域电磁测深[M].北京:地质出版社,1990.

[3] 彭仲秋.瞬变电磁场[M].北京:高等教育出版社,1989.

[4] Korjenevsky A V,Cherepenin V,Sapetsky S.Magnetic induction tomography:experimental realization[J].Physiological&Measurement,2000,21(1):89-94.

[5] 刘冀成,黄卡玛,华伟.基于遗传算法的磁聚焦线圈设计与场分布计算[J].成都理工大学学报,2004,31(4):412-417.

[6] 傅林,黄卡玛,向胜昭.生物组织磁聚焦电导率成像原理及反演算法[J].电波科学学报,2006,21(2):249-254.

[7] 刘冀成.基于改进遗传算法的生物电磁成像与磁场聚焦应用研究[D].成都:四川大学博士学位论文,2005.

[8] 李景天,郑勤红.矩形线圈的磁场计算[J].云南师范大学学报,2006,17(1):60-64.

[9] 邝向军.矩形载流线圈的空间磁场计算[J].四川理工学院学报,2006,19(1):17-20.

[10] 杨勇,陈德胜,刘冀成,等.管道金属蚀失量检测聚焦信号加载理论研究[J].油气储运2012,31(8):601-604.

[11] 朱平.圆电流空间磁场分布[J].大学物理,2005,9(24):13-17.

[12] 曾令宏,张之翔.圆形电流的磁场以及两共轴圆环电流之间的相互作用力[J].大学物理,2002,9(21):14-16.

[13] 向裕民.圆环电流磁场的普遍分布[J].大学物理,1999,18(1):14-17.

[14] 邝向军.方形载流线圈的空间磁场计算[J].物理与工程,2006,16(1):18-21.

[15] 段玉倩,贺家李.遗传算法及其改进[J].电力系统及其自动化学报,1998,10(1):39-52.

[16] 黄佳柏,王淑英.瞬变电磁法在埋地钢质管道腐蚀检测中的应用[J].石油化工腐蚀与防护,2001,18(4):39-43.