满足特定平方和指标平衡布尔函数的性质分析

周 宇

(保密通信重点实验室,四川成都610041)

0 引言

密码函数主要用在通信和密码等领域,布尔函数是密码函数中使用最广泛的一类密码函数。布尔函数的全局雪崩准则是基于扩散准则。为了克服扩散准则在某些点(局部性)上的自相关值,使布尔函数在整体上达到最优,1995年,Zhang Xianmo和Zheng Yuliang发现扩散性只能用来刻画布尔函数在部分点的自相关值,而对其他点没有要求,所以提出密码函数的全局雪崩准则(GAC)[1]:绝对值指标和平方和指标。GAC的提出,使人们对SAC和PC有了更为理性的思考。SAC和PC对某些点上的自相关值要求苛刻,而对其它点却不加限制,这导致密码函数的局部安全性。而GAC从全局着眼,对所有点的自相关值都提出了要求。2010年周宇等[2]提出了互相关函数的全局雪崩准则,将GAC指标推广到两个不同的布尔函数之间,得到这个准则的上下界,同时也得到该指标与高阶非线性度的关系。这两个概念为进一步研究提出了新的研究方向,在设计和分析中如何去找到这类指标较小的平衡布尔函数是值得研究的课题之一。

文中从两类达到较小的平方和指标的平衡布尔函数入手,研究对应的绝对值指标的下界,并对小变元函数给出其下界值。

1 基本概念

n元布尔函数f(x)是指从 Fn2到F2的一个映射,Bn表示所有n元布尔函数的全体。1995年Zhang和Zheng提出全局雪崩准则(GAC)。

定义1 设 f(x)∈Bn,则f(x)的平方和指标定义为[1]:

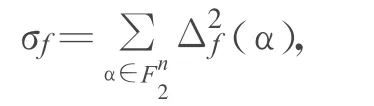
f(x)的绝对值指标定义为:

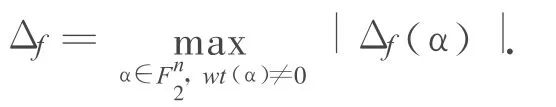
其中 f(x)的自相关函数定义为

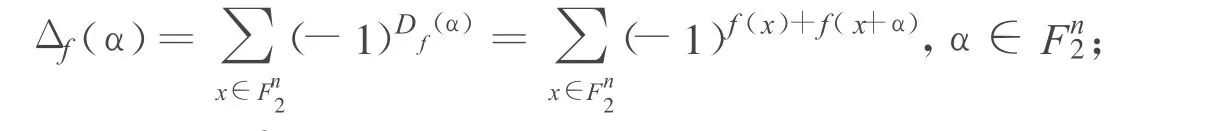
2010年周宇等[2]将此推广到两个不同的布尔函数之间,引入互相关所对应的全局雪崩准则。

定义2 设 f(x),g(x)∈Bn,则 f(x)和g(x)的互相关平方和指标定义为:

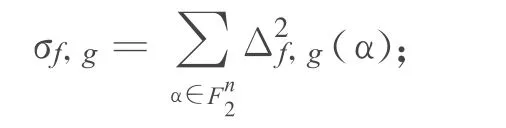
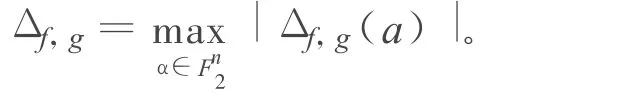
2 主要结果

Zhang Xianmo和Zheng Yuliang在研究GAC指标时,对一个布尔函数f(x)∈Bn的扩散补集A(所有非扩散点形成的集合,称为扩散补集)进行分析时,得到:

第一类函数:当 #A=2,变元 n为奇数时σf=22n+1。

第二类函数:当 #A=4,变元 n为偶数时σf=22n+2。

对每一类函数,都得到对应的函数表达式,但是这两类函数有其局限性,这是由于研究的都是几乎扩散函数(即在几乎所有的点(排除非零点)上都满足扩散性),一方面我们知道bent函数在所有点(排除非零点)上都满足扩散性,但bent函数是非平衡的,算法设计中为了满足Golomb伪随机性,一般要求密码部件是平衡的。另一方面,扩散点也不能太多,这种几乎扩散函数在密码算法中是不适用的,因为扩散性越好其对应的代数免疫性越低,这样就不能抵抗代数攻击。所以这里考虑一般的函数。

JSeberry和Zhang Xianmo等[3]在研究平衡布尔函数的非线性度和扩散时对变元为奇数的情况,给出#A=5的平方和指标,进一步印证上述结果。同时周宇等[4]在2012年提出一种基于修改bent函数和不相交谱的方法的平衡布尔函数构造方法,得到了变元在偶数情况下其平方和指标可达到σf=22n+2。同时Stanica和Sung等[5]得到在偶数变元情况下平方和指标达到σf=22n+2的平衡布尔函数,但是这些构造方法都没有给出在一般情况下相反的问题:即平方和指标达到σf=22n+2时对应的平衡布尔函数的绝对值指标。

文中就这两类函数进行分析。

引理1 设 f(x)∈Bn(n≥3),wt(f)≡0 mod 2。则对任意的 α∈ Fn2有 Δf(α)≡0 mod 8。

引理2[2]设f(x)∈Bn(n≥3),则

首先分析第一类满足 σf=22n+1的平衡布尔函数的绝对值指标的下界。

定理1 设 f(x)∈ Bn(n ≥3)且 wt(f)=2n-1,t=#{α∈ Fn2:Δf(α)≠0}。若 σf=22n+1,则

(i)t≥1;

证明 由于 f(x)是平衡函数,在引理1的基础上,为了方便分析设 Δf(αi)=8·li(li∈Z,0≤i≤2n-1),这里 αi∈ Fn2。则根据引理2可知

进一步在不引起混淆的情况下设 l0=α0=(0,0,…,0)为 Fn2中0向量,此时对应的 Δf(α0)=2n,对其它的做如下假设(这个假设不影响对问题的分析):li≠0(1≤i≤t),li=0(t+1≤i≤2n-1)。则式(1)简化为:

当 σf=22n+1时 ,有

可知

分两方面讨论:

注解1:定理1表明

(i)f(x)至少有1个扩散点;

表1 定理1中平衡布尔函数的 Δf下界

表1表明:当7≤n≤30时,Δf下界至少大于2n/2。

推论1 设 f(x)∈Bn(n≥3)且 wt(f)=2n-1,σf=22n+1。若满足 m阶扩散准则,则

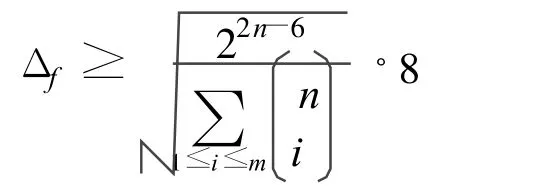
特别地,在分组密码的S盒中用得最多的是8入8出,这里就对 n=8元平衡布尔函数进行分析,得到对应的下界,见表2。

表2 8元平衡布尔函数的 Δf下界

注意:m=8对应的是bent函数,是非平衡的,这里不考虑。

在设计一个布尔函数时希望绝对值指标 Δf越小越好,根据表2可知扩散阶越高越好,但同时也考虑其它密码学指标,例如代数免疫、相关免疫、代数厚度等,而不能仅仅认为扩散阶越高越好。

其次分析第二类满足 σf=22n+2的平衡布尔函数的绝对值指标的下界。

定理2 设 f(x)∈ Bn(n ≥3)且 wt(f)=2n-1,t=#{α∈ Fn2:Δf(α)≠0}。若 σf=22n+2,则

(i)t≥1;

证明 在定理1的基础上,当 σf=22n+2时,有

可知

分两方面讨论:

注解2:定理2表明

(i)f(x)至少有1个扩散点;

推论2 设 f(x)∈Bn(n≥3)且 wt(f)=2n-1,σf=22n+1。若满足 m阶扩散准则,则

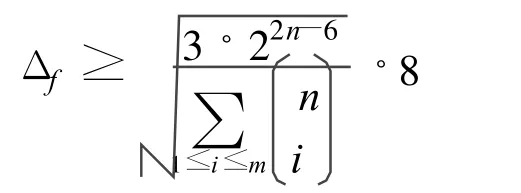
注解3:定理1和定理2的结果改进了Sung等[6]对满足一定扩散阶的平衡布尔函数的平方和指标下界,文中给出绝对值指标的下界。同时周宇等在文献[7]中给出这类函数的自相关分布特征。结合Zhang Xianmo和Zheng Yuliang在文献[8]中的结果,可知定理1和定理2中t=3,6时是不存在这样的函数;t=4时变元n为偶数;t=5时变元 n为奇数。

最后考虑t取特殊值的情况:

推论3 设 f(x)∈ Bn(n≥3)且 wt(f)=2n-1,t=#{α∈ Fn2:Δf(α)≠0},t=4。

(i)若 σf=22n+1,则对任意的 α∈Fn2有|Δf(α)|∈{2n-1,0}。此时有 Δf=2n-1。

(ii)若σf=22n+2,则不存在这样的平衡布尔函数。

3 结束语

达到一定的平方和指标的布尔函数是序列密码中的一个研究方向,文中给出2类达到较小平方和指标的布尔函数的绝对值指标的下界,对密码函数部件的设计和分析有一定理论指导,这些结果改进了已有的一些结果,所以在后续研究中重点是如何去构造这类达到最小平方和指标的布尔函数。同时还应当考虑具有相同平方和指标(或者相同自相关分布[9])的布尔函数密码学性质,这些对设计实用的布尔函数具有重要的意义。

[1] X M Zhang,Y L Zheng.GAC—the criterion for global avalanche characteristics of cryptographic functions[J].Journal for Universal Computer Science,1995,(5):316-333.

[2] Yu Zhou,Min Xie,Guozhen Xiao.On the global avalanche characteristics of two Boolean functions and the higher order nonlinearity[J].Information Sciences,2010,180:256-265.

[3] J Seberry,X M Zhang,Y Zheng.Nonlinearity balanced Boolean functions and their propagation characteristics[C].In Advancesin Cryplogy-CRYPTO'93,LNCS.773:49-60,Springer-Verlag,Berlin,Heidelberg,New York,1994.

[4] Yu Zhou,Xinfeng Dong,Wenzheng Zhang,et al.New bounds on the sum-of-squares indicator,Communications and Networking in China[R].ChinaCom 2012.Fourth International Conference,8-10,Aug,2013:173-178.

[5] P Stanica S H Sung.Improving the nonlinearity of certain balanced Boolean functions with good local and global avalanche characteristics[J].Information Processing Letters,2001,79:167-172.

[6] S H Sung,S Chee,C Park.Global avalanche characteristics and propagation criterion of balanced Boolean functions[J].Information Processing Letters,1999,69:21-24.

[7] Yu Zhou,Weiguo Zhang,Juan Li,et al.The auto-correlation distribution of balanced Boolean functions[J].Frontier of Computer Sciences,2013,7(3):272-278.

[8] X M Zhang,Y L Zheng.Characterizing the structures of cryptographic functions satisfying the propagation criterion for almost all vectors[J].Designs,Codes and Cryptography.1996,7:111-134.

[9] Yu Zhou.On the distribution of auto-correlation value of balanced Boolean functions[J].Advances in Mathematics of Communications,2013,7(2):335-347.