含软弱夹层的某公路边坡开挖支护数值模拟分析

陈 婷，赵 川，吴宇峰*

(西华大学 能源与环境学院，成都 610039)

对边坡分级开挖过程中的应力应变动态变化的研究，传统方法是采用刚体极限平衡法，此法需对复杂岩体边坡作一定程度的简化［1］。对于土质边坡，圆弧形、折线形算法的计算结果在工程界能够得到广泛的认可，但对于岩质边坡，因其破坏失稳机理、模式、滑面形状抗剪参数取值等条件的不同而存在争议。近年来，有限元数值分析法在边坡的稳定性分析和评价中得到广泛应用，其用于边坡分析的基本原理是将一个连续的边坡体变换成离散的单元组合体，利用网格剖分将边坡(一般采用二维)剖面体系在形式上划分为有限个单元体。并假定各单元均为均质、连续、各向同性的完全弹性体，保持自己的介质特征，有自己的物理力学参数，各单元由节点相互连接，边坡岩体的内力和外力由节点来传递［2］。

通过有限元计算分析，可以获取位移、应力分布状况，绘制应力等值线，并通过对边坡非线性有限元模型进行强度折减，使边坡在达到不稳定状态时，非线性有限元静力计算不收敛，此时的折减系数就是稳定安全系数。同时可得到边坡破坏时的滑动面，与极限平衡法相比具有相对优势。

本文基于有限元法，对某公路边坡的开挖支护过程进行模拟分析。实际边坡工程中软弱结构往往是边坡破坏的控制因素，因此本文在计算中考虑了岩土体中软弱夹层的影响，使计算结果更符合实际工程。

1 工程背景

某高速公路丘陵路段分布广泛的沉积岩及其变质岩，岩层倾角为25～45°。高速公路路堑边坡的开挖坡角大于岩层层面倾角，边坡开挖形成大范围的临空面。由于边坡开挖速度快、临空面高、开挖坡度陡，导致坡角部位应力集中现象严重，存在潜在的破坏动力，因此在施工过程中应注意采取及时的加固措施。

2 计算方法

2.1 强度折减法

有限元计算中边坡的稳定安全系数一般通过强度折减法进行计算。强度折减法认为:边坡岩土体发生剪切破坏的原因是其所受剪应力达到极限抗剪强度，计算中将坡体的真实抗剪强度除以折减系数F，以达到强度折减的目的。当达到极限破坏状态时，此时的F即为边坡的稳定安全系数［3-7］，其计算公式为:

其中:c和φ为岩土体真实的粘聚力和内摩擦角;c＇和φ＇为折减后的粘聚力和内摩擦角。

2.2 计算模型及岩体力学参数

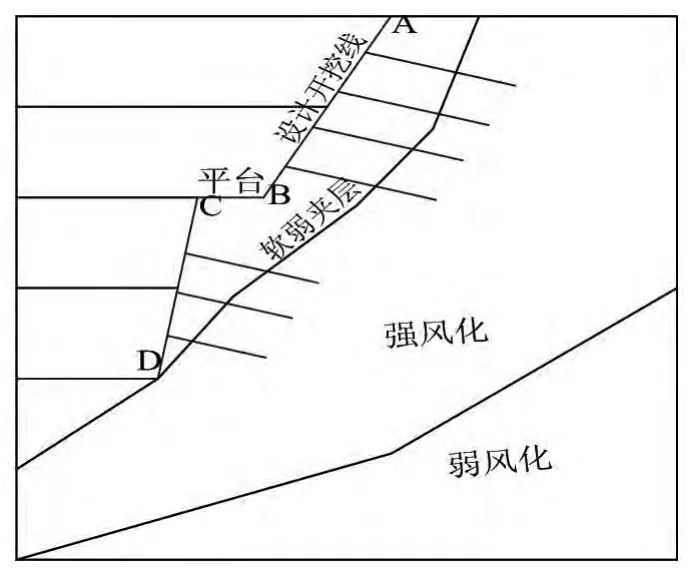
图1 开挖剖面

分析范围选取水平方向取30 m，竖直方向取30 m，开挖坡角分别为60°和80°，分4级开挖，每次开挖5 m，总开挖高度20 m。加固措施选取锚喷支护，锚杆直径22 mm，与水平夹角15°，每根锚杆施加150 kN预应力。喷射混凝土强度等级为C25，厚度20 cm。为方便监测边坡开挖时应力应变规律，在坡面附近选取4个监测点A、B、C、D。具体计算剖面如图1所示。计算剖面确定后，建立有限元网格模型，为了保证计算的准确性，在边坡开挖附近区域应进行网格加密，如图2所示。材料模型为Mohr-Coulomb弹塑性模型，软弱夹层采用界面单元模拟，混凝土喷层利用板单元模拟，输入相应的材料属性即可。

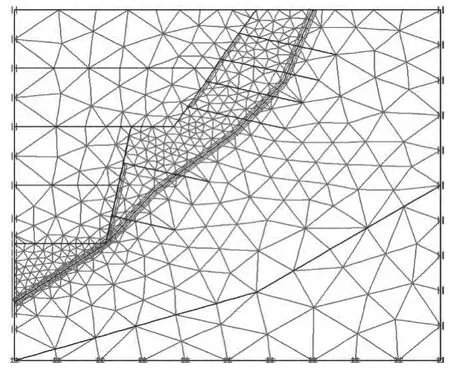
图2 有限元网格模型

建立好计算模型后，需对岩土参数进行选取。计算参数的选取将直接影响计算结果的精度，因此，根据现场试验和室内试验数据、工程地质类比法、边坡临界失稳状态逆分析法，并不断修正岩土计算参数，得到具体岩体参数如表1所示。

表1 岩土体物理力学参数

2.3 基本假定

为了便于建立分析模型，结合该边坡工程的实际情况，做如下假定:1)由于没有准确的初始地应力资料，所以只考虑岩体的自重应力，忽略其构造应力;2)遵循二维平面应变假定;3)在模拟计算过程中，不考虑地下水的影响。

2.4 计算工况选取

1)只开挖不支护。此时，为了真实模拟实际情况，计算过程中应将锚杆单元和板单元冻结，激活软弱夹层的界面单元。

2)开挖并及时支护。每一步开挖后应激活相应部位的锚杆单元和板单元，以此模拟所采取的加固措施，如此重复进行，直到边坡开挖完成。

3 计算结果及分析

3.1 位移分析

规定水平位移向左为正，向右为负。图3和图4给出了不同开挖工况和不同计算步的测点水平位移变化规律，由图可知:工况1中边坡进行开挖，将导致4个测点不同程度地发生向左水平位移，即有下滑趋势，其中以B、C点较明显，前3级开挖完成后水平位移均为-18 mm，而开挖至第4级后，B、C位移分别增长到-36 mm和-37 mm，说明开挖至第4级后，边坡的整体稳定性将受到很大影响。分析其原因，是受到软弱夹层的影响，第4级开挖将导致软弱夹层露出，而此软弱结构面破坏了岩体的连续性，使得软弱夹层外部岩体发生整体滑移，如图5所示。通过分析认为:在不支护的情况下，开挖前15 m边坡能保持稳定，而开挖最后5 m时边坡将向左发生很大水平位移，此时可认为边坡已破坏。

图3 工况1边坡x方向位移

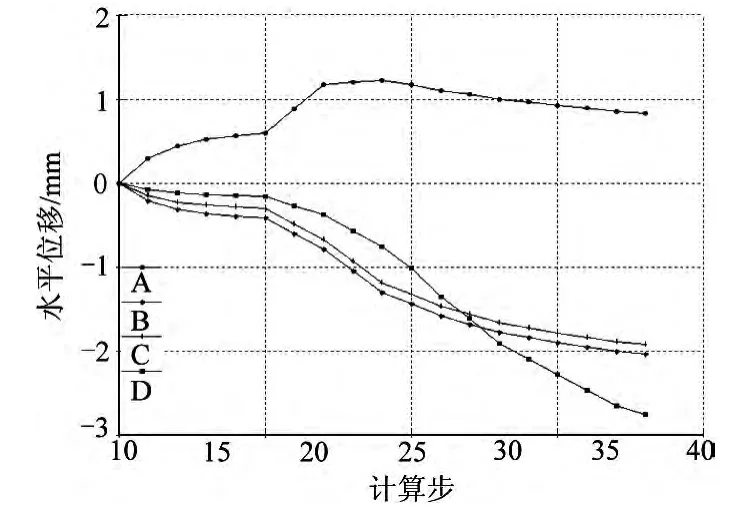
图4 工况2边坡x方向位移

图5 开挖不支护边坡整体水平位移

本文还计算了边开挖边支护的工况2。结果如图4和图6所示，B、C点最后的位移分别为-20.25 mm和-18 mm，比不支护开挖时减小了20 mm左右。从图3和图4分析可知:不支护时A点最后发生向边坡外部临空方向位移，最大值可达-1.59 mm;而当支护后，由于添加预应力锚杆后，锚杆收缩，通过混凝土喷层传递锚固力，使得A点发生面向边坡内部方向的位移，最后值为8.37 mm，有利于边坡的稳定。位于坡脚处D点，支护后位移反而有所增大，究其原因，由于软弱夹层贯穿整个边坡，而添加锚杆部位仅位于软弱夹层的上部，提高了上部边坡的稳定性，而位于边坡下部的软弱夹层带并未采取加固措施，从图6可知，坡脚D点附近区域岩体发生拉破坏，所以上部支护后，位于下部坡脚的D点位移反而有所增大。分析表明，对于此类软弱夹层贯穿的边坡，在实际开挖过程中，除了对上部边坡进行及时支护外，位于边坡底部和深部的软弱夹层附近岩体也有必要采取一定的加固措施，防止边坡坡脚处岩体发生局部破坏，提高边坡整体稳定。

图6中的边坡整体水平位移与图5相比得到了有效控制，平台附近大范围区域水平位移减小，极值由-39.94 mm减小到-27.49 mm，说明支护效果明显。

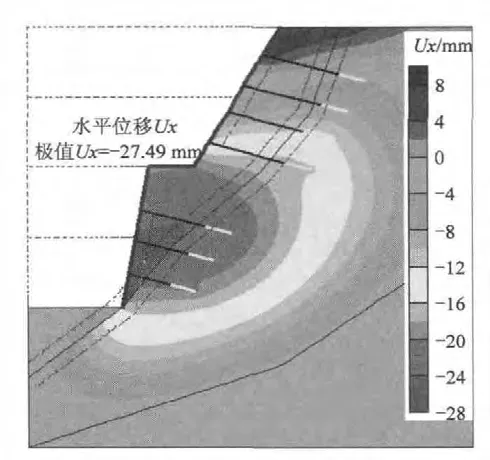
图6 开挖及时支护后边坡整体水平位移

3.2 塑形区域分析

图7 开挖不支护边坡塑性点分布

图8 开挖及时支护后边坡塑性点分布

边坡稳定性分析中，塑性区范围大小常用来反映边坡的破坏程度。图7和图8分别给出了2种不同开挖工况下边坡的塑性区域分布情况。(深色点代表塑性点，浅色点表示拉伸截断点)。

由图7可知，当边坡开挖不进行支护时，塑形区沿着软弱夹层分布，并且在中上部位出现拉伸截断点，说明部分岩体所受拉应力超过其抗拉强度，岩体中将产生小裂隙。而当边坡开挖支护后，由图8可以明显看出，边坡软弱夹层上部范围内岩体的塑性点和拉断点均消失，仅在边坡中下部位少量存在，有向深层发展的趋势。

3.3 稳定安全系数分析

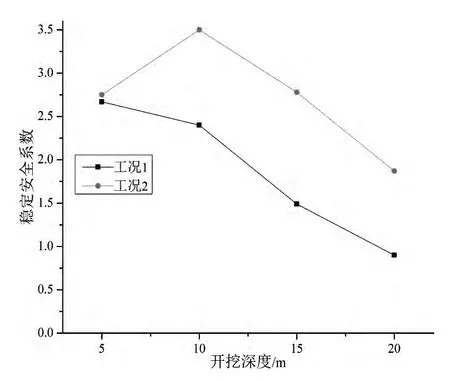
图9 2种工况稳定安全系数对比

为进一步对不同工况下边坡开挖稳定性进行分析，图9给出了不支护开挖和开挖及时支护的不同开挖深度的安全系数。分析发现，2种工况下，随着开挖深度的增加，安全系数均有降低的趋势。在工况1中，安全系数降低很快，且最终小于1，表示边坡开挖完成后并不能保持自身稳定，将发生滑坡;工况2中，因在开挖过程中及时采取了加固措施，各开挖深度边坡的安全系数均有较大增长，且最后开挖完成后达到1.87，满足工程要求。

以上分析与前文中对位移和塑性区分析所呈现的现象具有一致性，证明了分析结果的可靠性。

4 结语

本文基于有限元法对某公路边坡的开挖支护过程进行了数值模拟分析，研究发现:1)边坡开挖如果不采取支护措施，边坡软弱夹层外部岩体将发生整体向外位移，且主要集中在平台附近区域。开挖完成后，安全系数小于1，边坡将处于失稳状态，通过塑性贯通区确定了滑裂面，说明开挖过程中采取支护措施是很有必要的。2)当开挖过程进行支护后，危险区域发生的大位移得到有效控制，边坡软弱夹层上部范围内岩体的塑性点和拉断点均消失，仅在边坡中下部位少量存在，安全系数明显增大，开挖支护完成后达到1.87，满足工程需要。

综上所述，对边坡开挖支护过程进行模拟分析，可以得到不同开挖阶段和不同工况的应力应变、位移、塑性变形区和稳定安全系数，可以优化施工方案，有效快速地确定支护时间和支护位置。

［1］黄梦宏，丁桦.边坡稳定性分析极限平衡法的简化条件［J］.岩石力学与工程学报，2006，25(12):2529-2536.

［2］王汉辉.边坡稳定的有限元塑性极限分析法研究［D］.武汉:武汉大学，2003.

［3］赵尚毅，郑颖人，邓卫东.用有限元强度折减法进行节理岩质边坡稳定性分析［J］.岩石力学与工程学报，2003，22(2):254-260.

［4］郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2004，23(19):3381-3388.

［5］杨静，何江达，胡德金.土质边坡稳定分析中条分法与有限元法的比较［J］.四川水力发电，2003，22(1):27-29.

［6］郑颖人，赵尚毅，张鲁渝.用有限元强度折减法进行边坡稳定分析［J］.中国工程科学，2002，4(10):57-61.

［7］刘小丽，周德培.有软弱夹层岩体边坡的稳定性评价［J］.西南交通大学学报，2002，37(4):382-386.