土工格室柔性结构体系处治桥头跳车数值模拟研究

闫 茜，杨广庆

(1.中铁第五勘察设计院集团有限公司，北京 102600;2.石家庄铁道大学，石家庄 050043)

在高速公路的各种病害中，桥头跳车现象是常见的病害之一，也是多年来困扰公路行业的一大难题。桥头跳车的存在，会使车辆在通过路桥连接处时产生跳动和冲击，对桥梁和路面造成附加冲击，并且车速大幅减低，会使司乘人员感到颠簸不适，严重时甚至导致车辆失控而发生交通事故。对桥头路面大量的维修养护不仅需花费大量人力、物力和财力，而且还会产生不良的社会影响。工程实践中已积累了多种方式方法用于改善桥头跳车现象，土工格室的加筋即是其中有效的一种。

1 计算模型

运用ADINA非线性有限元计算软件，采用路堤与地基的三维模型进行计算，模型基于高速公路土工格室柔性结构体系的布置方式而建立。结合工程实践，取路堤高度4 m，横断面为梯形，两侧边坡坡度均为1∶1.5，路堤顶面宽34.5 m，底面宽46.8 m。土工格室以楔形等间距布设，坡度1∶2，总计五层，除顶层高度为20 cm外，其余各层高度均为10 cm。其中，路基底面一层铺设长度30 m，向上每层依次递减2 m，直至路基顶面一层为30 m，如图1所示。各层土工格室均与桥台刚性联接，各土工格室层间为路基填土。

为分析土工格室加筋区域与普通路堤填土区域的应力与沉降性状差异，模型中取线路纵向长度40 m，远离台背的末端10 m用于进行加筋和未加筋时路堤及地基受力变形状态对比。

取软土地基深15 m，计算长度亦为40 m(线路纵向)，计算宽度取至边坡两侧各20 m范围内。计算模型的几何示意见图1。

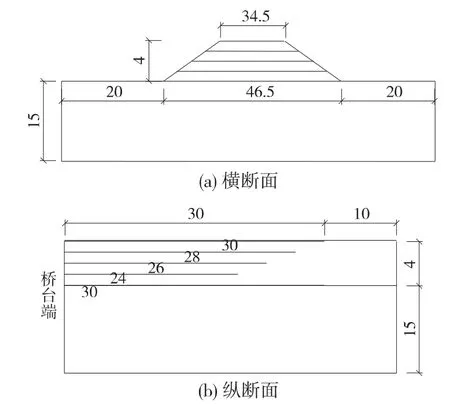
图1 计算模型的几何示意(单位:m)

1.1 材料本构关系

计算模型中结构材料的本构关系可分为三类。

(1)地基土、路堤填土:采用ADINA所提供的“岩土材料”中的摩尔-库仑(Mohr-Coulomb)模型来模拟，基于理想塑性摩尔-库仑屈服函数、非相关流动法则、拉伸截止。因应力应变准则选为小位移/小应变，程序采用“材料非线性公式”计算。通过输入弹性模量、泊松比、密度、内摩擦角、黏聚力、拉伸截止极限以及膨胀角选项来定义材料属性。

(2)土工格室结构层:采用弹性材料模型，这种材料模型适用于小应变分析，能够在一定的简化条件下模拟结构层的力学性质。通过指定弹性模量、泊松比、密度来定义材料属性。

(3)路堤边坡:因路堤边坡一般采用混凝土锚喷支护，故选择各向同性线弹性材料模型来模拟路堤边坡，通过设定弹性模量、泊松比、密度和热膨胀系数(缺省为0)来定义材料属性。

1.2 材料参数

模型中各部分材料的参数选择见表1。

表1 材料参数

1.3 工程条件的模拟

对地基施加自重荷载，通过调节地基土单元组G1的泊松比、弹性模量、重度、内摩擦角和黏聚力，来模拟实际工程中不同的地基条件。

不同格室结构层的模拟，通过改变格室结构层单元组G3的弹性模量和泊松比，来模拟不同高度的土工格室结构层。

对路堤施加自重荷载，通过改变路堤填土单元组G2的内摩擦角、黏聚力、重度和泊松比，来模拟不同的路基填料。

1.4 网格划分及边界条件

以ADINA中提供的按细分份数的方式对三维模型进行网格划分，单元类型采用八节点六面体单元。网格密度控制原则为，综合考虑x、y、z 3个方向尺寸，使划分的每一八节点六面体单元的长宽比在1∶3～1∶5范围内。

采用ADINA中提供的“自由度边界条件”，通过控制节点的各自由度状态为“固定”(Fixed)或“自由”(Free)来定义模型中各边界条件。将各边界物理条件施加在边界面(surface)上，这样边界条件的定义简单明了，同时不受单元网格变化的影响。计算模型中各边界条件见表2。

1.5 定义单元组

根据与实践工程结合的需要，计算中将地基与路堤结构划分为四个单元组。

(1)Group1:地基。采用3D实体单元。

(2)Group2:路基填土。采用3D实体单元。

(3)Group3:格室结构层。考虑到格室结构层的高度为10～20 cm，与地基土体厚度15 m和路基填土的高度50 cm～1 m相比起来很小，若采用3D实体单元，层间高度相差过大，在划分网格时难以合理平衡单元三个方向的尺寸比例，而土工格室结构层又与桥台刚性连接，故考虑将格室结构层赋为具有一定厚度的壳单元组(shell)，可在一定条件下模拟格室结构层的受力变形性状，易于合理定义网格密度和划分单元。

表2 边界条件

(4)Group4:边坡支护。与隧道衬砌结构相类似，模型中边坡支护结构采用具有一定厚度的壳单元(shell)，厚度取为40 cm。因支护结构通常采用混凝土锚喷，此单元组选用线弹性材料模型。

1.6 施加荷载

模型中全部结构均依据已定义的材料密度参数施加自重荷载，将未建入模型的路面结构层简化为施加在模型顶面的均布荷载，以ADINA中所提供的Pressure形式施加。取路面结构层高度为0.65 m，面层为混凝土，重度24 kN/m3，基层为水泥稳定碎石土，重度约23 kN/m3。计算后取等效路面结构层均布荷载为16 kPa。荷载施加于路堤结构的全顶面上。

1.7 分析与求解

对于土工格室加筋路堤的受力变形分析是非线性分析过程。因土体的弹塑性本构关系均以增量形式表示，故本计算采用增量迭代法，使用完全牛顿法求解，在每一个增量步内使用完全牛顿法进行迭代。收敛准则采用能量收敛准则。应力应变准则采用小变形小位移。

根据以上所述建立加筋路堤与地基的三维计算模型。将路堤底面中轴线与桥台的交点建在坐标原点处，整个模型关于x-z坐标面对称，路堤与桥台连接端置于y-z坐标面，以x轴为线路纵向，其中x轴负方向为远离桥台方向。

所建立几何模型及网格划分、边界条件、施加荷载如图2所示。

2 计算结果分析

2.1 加筋对路堤本体沉降的影响

加筋前后路堤顶面中轴线沉降曲线对比如图3所示。

图2 计算模型及荷载

图3 加筋前后路堤顶面沉降对比

从图3中可看出，路桥过渡段的路堤未经加筋处治时，台后路堤顶面沉降呈一直线，沉降值约为0.072 m，与桥台之间没有过渡，容易引起路桥联接路段的台阶形沉降，引发桥头跳车等病害。土工格室加筋处理后，在土工格室加筋处治区(台后30 m内)，台后路堤顶面沉降呈抛物线状，由零值缓慢、平滑地过渡到未处理区的较大沉降值。且处理区段内的最大沉降值为0.069 m，低于未加筋路堤。这说明，土工格室结构层对于台后路堤的加筋处治，可有效减小路堤顶面沉降，并实现桥台与路堤间沉降差异的平稳过渡，改善桥头跳车现象。

加筋前后路堤底面沉降之对比如图4所示。

图4 加筋前后路堤底面沉降对比

加筋后，路堤下软土地基的沉降也呈现出明显的过渡区域，且在加筋范围(30 m)内，软基表面的竖向沉降值远小于不加筋时。这说明，土工格室的加筋不仅能有效过渡路堤顶面沉降，而且能有效减小和过渡下卧软基的竖向变形，减小基础的最终沉降量，利于路堤本体的稳定。因此，采用土工格室柔性结构体系加筋于台后路堤的处理方法对于平衡路桥过渡段的差异沉降是有效、可行的。同时，与刚性的钢筋混凝土搭板处治方法相比，避免了刚性搭板处理区与其后未处理区在衔接处可能出现的二次跳车现象，也避免了在车辆荷载反复作用下可能出现的搭板断裂问题，利于路桥衔接段沉降的平顺过渡。

2.2 加筋对下卧软基水平位移的影响

以距离桥台2 m(靠近台背端)和16 m(加筋区域中部)处为代表性位置，对比不同位置处加筋前后路堤坡脚下地基水平位移。各处路堤坡脚垂线下软土地基水平位移随深度的变化在加筋前后之对比如图5所示。

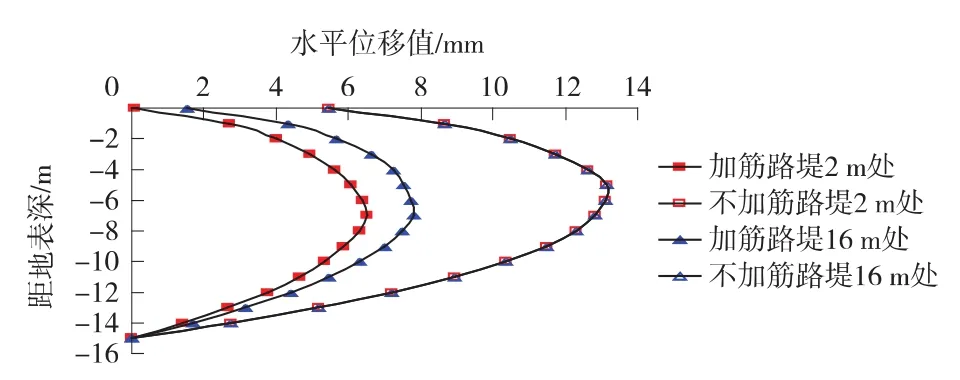
图5 加筋前后坡脚下地基水平位移对比

在土工格室加筋体系中，因格室模量远大于周围土体，再加上格室侧壁所发挥的侧限作用和摩擦作用，能够给土体提供一个强大的侧向限制作用，从而有效减小地基土体的水平位移，从图5中可得到如下结果。

(1)土工格室加筋明显减小了下卧软基土体的水平位移。未加筋时，坡脚下地基土体的水平位移最大值为13.2 mm，加筋后，坡脚下土体最大水平位移为7.8 mm，减小了约41%，这说明，通过格室与周围土体的摩擦和紧箍作用的发挥，加筋体有效限制了土体变形，限制了地基土体的侧向位移，使得下卧软弱地基的整体性得到增强。

(2)地基土体的水平位移最大值并非在坡脚地表处，而是发生在地表下一定深度。由图5中看到，未加筋时，下卧软基最大水平位移发生在离地表深5 m处，加筋后，最大水平位移的发生深度在地表下约7.1 m处，这就是说，格室加筋明显限制了地基土体的侧向变形，改变了下卧软基的位移场分布，将地基最大水平位移发生位置向更深处发展，提高了地基土体的整体稳定。

(3)对于不加筋路堤来说，与台背不同距离处坡脚下软基水平位移的分布无明显差别，但加筋路堤则有差别。靠近桥台固定端(2 m位置处)地基土体水平位移程度较小，而加筋区域的中部(16 m位置处)则相对较大，这是由于格室结构体系的各层均与桥台刚性连接，对周围土体的侧限作用非常明显，逐层减弱土体侧向变形，从而减小了桥台端地基土体的水平位移。

2.3 加筋对下卧软基竖向位移的影响

选取加筋区域的中部，与台背距离16 m处作为代表点，对加筋前后地基土体的竖向位移进行分析。由对称性，取路堤及地基的一半进行分析，两种结构形式下的地基竖向位移等值线图见图6。

图6 加筋前后地基竖向位移等值线图

由图6中看到，加筋前后地基土体竖向位移的分布形态相似，但加筋路堤能够在一定程度上减小地基沉降量，未加筋路堤下地基最大竖向位移值由加筋前的6.2 cm减小到5.5 cm，减小了约11%。路堤中的土工格室柔性结构层开始承担土体中一部分拉力，降低了传至地基表面的应力，减小了路堤范围下地基的竖向变形，使得地基的沉降分布区域均匀，并使地基的变形区域缩小。

该位置处加筋前后地表各点竖向位移分布如图7所示。

图7 加筋前后地表各点竖向位移对比

(1)加筋前后，地表各点的竖向位移分布呈现相似形态，加筋时的曲线变化更加均匀、平缓。

(2)加筋对地基表面不同位置的各点竖向位移均有削减。地表竖向位移最大值，不加筋时为6.2 cm，加筋后为5.5 cm，减小了约11%。并且，不仅是路堤范围内地表竖向位移被减弱，坡脚(距中轴线23.25 m)外一定范围内的地表各点竖向变形都明显减小，且变化更平缓。路堤和地基的竖向变形减小，整体性得到增强。

(3)加筋前后，坡脚外地表隆起范围(竖向位移为正值的区域)相差不大，隆起的程度也几乎无差别，约2～3 mm，土工格室加筋后的地表竖向位移零点比未加筋时更加靠近坡脚。

2.4 加筋对地基竖向应力的影响

选取路堤加筋区域的中部，与台背距离16 m处作为代表位置，考察加筋前后地基顶面竖向应力变化情况，如图8所示。

图8 加筋前后地基顶面竖向应力对比

从图8中看到，加筋前后地基顶面竖向应力分布形态相似，但格室加筋很明显地降低了地表各点竖向应力水平。在路堤中轴线处，加筋前的地基顶面竖向应力值为78.5 kPa，格室加筋后大幅降至46.6 kPa，降低幅度约41%。由此可见，使用具有一定高度和刚度的土工格室柔性结构体系加筋处理后，多层连续格室充分发挥了对周围土体的约束作用和紧箍作用，将上部路堤传来的荷载充分扩散，降低了地基表面应力水平，使其无论是在路堤中轴线还是坡脚附近都明显小于不加筋的结构。

而在路堤中轴线处，地基表面的竖向应力随与桥台距离而变化的曲线如图9所示。

图9 加筋前后中轴线处地基顶面竖向应力对比

由图9中看出，土工格室加筋前后地基表面竖向应力的分布形态发生了很大改变。加筋范围内，地基表面处土中竖向应力较之加筋前有明显减小，且分布平缓、均匀。未加筋时，地基顶面竖向应力为78.5 kPa，加筋后，加筋范围内的地表最大竖向应力降至49.6 kPa，减小了约37%。

而在加筋区域外，地基土体中竖向应力与未加筋时无明显差别。这说明具有强大抗拉强度与刚度的格室柔性结构体系明显发挥了扩散基底应力、改变地基应力场分布、降低基底应力水平的作用，基底应力的减小使得地基中所受附加应力也大大减小，台后加筋范围内的地基变形也减小。

2.5 加筋对地基剪应力的影响

距桥台16 m处加筋前后路堤中轴线下地基土体中各点最大剪应力随深度的分布对比如图10所示。

加筋前后地基土一点最大剪应力值的对比见表3。

图10 加筋前后中轴线处地基土体最大剪应力对比

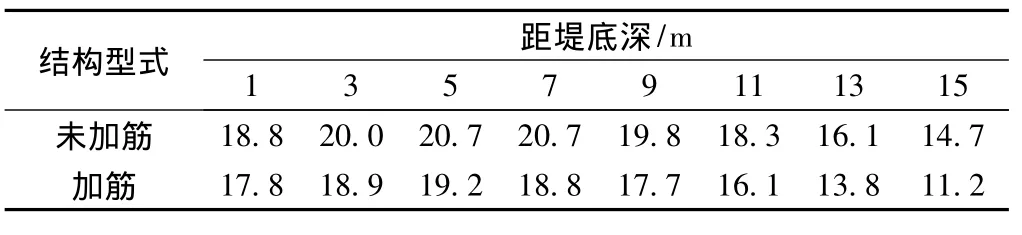
表3 地基土最大剪应力值对比 kPa

从图10中看到，在距桥台一定位置处，土工格室加筋路堤的地基各不同深度最大剪应力均明显小于未加筋结构。加筋时地基土体最大剪应力峰值19.2 kPa，比未加筋结构的峰值20.8 kPa降低了8%。这是由于在土工格室加筋路堤中，起加筋作用的筋材是具有一定高度的三维立体结构土工格室，与路堤填料和软基土体相比，无论在物理力学性质还是材料表面介质特性都有很大差别，于是在界面上能够产生强大的摩擦阻力和约束力，由此筋材对地基提供了一个很强的水平约束作用，相当于对地基施加了水平拉力影响，因而使得地基土体中最大剪应力明显减小。这就说明，加筋改变了地基土体应力场分布，降低了土体中剪应力水平，提高了地基土体承载能力。

3 加筋效果的影响因素分析

3.1 格室高度

保持模型其他材料参数均不变，见表1，分别取土工格室结构体系的单层高度为10 cm、20 cm、30 cm，格室结构层的弹性模量分别取为50 MPa、55 MPa、60 MPa，将三种情况的模拟计算结果对比分析。

路基顶面沉降曲线对比如图11所示。

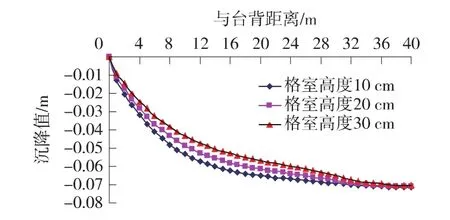
图11 不同高度土工格室加筋路基顶面沉降对比

由图11中可看出，加筋范围内，单层格室高度在一定程度上影响了路堤顶面沉降值，单层格室越高，结构层弹性模量越大，路堤顶面沉降越小;而加筋范围之外则无影响。这是由于单层格室高度越大，与格室周围土体的摩阻作用就越大，对土体变形的限制作用也越强，减小土体变形，在格室结构体系一层层消减变形的作用下，路堤本体的最终沉降量得到减小;同时，格室高度增大，在同样的路基填料条件下，每一格室结构层的弹性模量和抗弯刚度也会随之增大，增强了加筋路堤整体抵抗变形的能力。

路基基底竖向应力对比见图12。

图12 不同格室高度下基底竖向应力对比

图12显示，随着土工格室高度及结构层弹性模量的提高，加筋路堤基底竖向应力值有所减小。这是由于格室高度的加大提高了格室结构层的抗拉压能力与抗弯刚度，其扩散均化竖向应力的能力得到增强，使得基底应力得以减小，提高了下卧软基的承载能力。

由以上分析可得，设计及施工中，选择片材弹性模量高、延伸率小的土工格室，适当加大土工格室的单层高度，利于提高结构体系的加筋效果。

3.2 地基土性质

保持土工格室的材质、间距、层数、填料性质均不变(见1.1～1.6)，改变地基土物理力学参数见表4。

表4 地基土的物理力学参数

考察三种地基条件下格室加筋路堤顶面沉降曲线，见图13。

图13 不同地基条件下加筋路堤沉降曲线

从图13中可看出，地基土的性质对土工格室加筋路堤沉降有着显著影响。地基土的弹性模量越大，内摩擦角和黏聚力越高，加筋路基的沉降值越小，沉降过渡越平缓。且在三种地基条件下，土工格室加筋路堤均能实现桥台与路堤沉降差异的缓慢过渡。

3.3 填料性质

保持计算模型中其他各项条件均不变(见1.1～1.6)，改变路基填料的弹性模量、内摩擦角、黏聚力以及重度，见表5。

表5 填料的物理力学参数

三种不同填料性质条件下路基沉降曲线及加筋区域基底竖向应力对比分别如图14和图15所示。

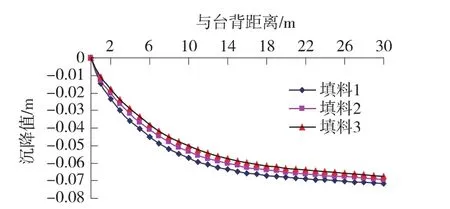
图14 不同填料条件下加筋路堤沉降曲线

图15 不同填料条件下基底竖向应力对比

由图14和图15可看出，填料性质的改变对于加筋路堤的沉降和基底应力均有所影响，但影响程度不大。随着填料弹性模量的提高和内摩擦角与粘聚力的增大，加筋路堤沉降和基底应力均有所减小，沉降坡更趋平缓，但变化并不明显。因此，在土工格室柔性结构体系加筋路堤中，多层连续铺设的格室体系与土体的摩擦及约束作用减弱了填料性质不良带来的不利影响，在保证压实度足够的条件下，注意施工质量的控制，仍可发挥良好的工程作用。

3.4 底层土工格室

在其余设计和参数完全相同的情况下(见1.1～1.6)，对铺设底层土工格室和不铺设底层土工格室的两种工况进行对比计算分析。计算得到的路基沉降与地基顶面竖向应力对比如图16和图17所示。

从图16可看出，有无底层土工格室对路基沉降影响不大，加筋范围内的铺设底层格室时的路堤沉降略小于无底层格室时，加筋范围外则几乎无差别。而图17则显示底层格室对于地表竖向应力的影响则较大，在加筋区域各不同位置处，底层格室的存在均使得地基表面应力明显小于无底层格室时情形，竖向应力最大值由74.8 kPa减至49.6 kPa，且分布更加平坦均匀。这就说明底层格室的铺设有助于整个格室结构体系均化、扩散应力作用的发挥，提高了浅层软弱地基的承载能力，同时减小其变形。

图16 有无底层土工格室时的路基沉降

图17 有无底层土工格室时的地表竖向应力

此外，底层格室有助于提高路堤与下卧软基刚度，增强其整体性，消减其变形，平缓过渡路桥差异变形。因此，在土工格室加筋路堤实践中，建议在路堤底部铺设格室。

4 结语

利用ADINA建立加筋路堤与地基的三维模型进行有限元计算，得出土工格室柔性结构体系的加筋效果主要表现如下。

(1)有效实现路桥衔接段路堤与桥台差异沉降的平顺过渡。

(2)减小下卧软基水平变形，将地基水平位移最大值发生位置向更深处发展。

(3)减小地基沉降量，使地基竖向位移分布趋于均匀。

(4)明显减小地基土体竖向应力，改变地基应力场，使应力分布更加均匀。

(5)发挥水平约束作用，显著降低地基土体剪应力。

(6)通过对格室高度、地基土、填料、底层格室等因素对土工格室加筋效果的影响的分析，得出:选择片材弹性模量高、延伸率小的土工格室，适当加大格室单层高度，并在路基底部铺设底层格室，有利于提高结构体系的加筋效果。

［1］ 杨晓华.土工格室工程性状及应用技术研究［D］.西安:长安大学，2006.

［2］ G.MADHAVI LATHA，et al.Experimental and Theoretical Investigations on Geocell-supported Embankments［J］.International Journal of Geotechnics，2006(1/2):30-35.

［3］ 李广信，陈轮，蔡飞.加筋土应力变形计算的新途径［J］.岩土工程学报，1994，16(3):46-53.

［4］ 冯忠居，方贻立.高等级公路桥头跳车的危害及其机理的分析［J］.西安公路交通大学学报，1999，19(4):33-35.

［5］ 傅舰锋.土工格室柔性结构层力学性状的试验研究［D］.西安:长安大学，2002.

［6］ 韩明.高速公路软土地基土工格室加筋路堤研究［D］.南京:东南大学，2004.

［7］ 周正兵.土工格室加筋软土地基的沉降变形与地基承载力研究［D］.武汉:武汉大学，2002.

［8］ 刘俊彦，罗强.土工格栅、土工格室加筋垫层对软土路基沉降控制效果的有限元分析［J］.铁道标准设计，2002(12):5-7.