基于采空区移动过程的残余变形推论
秦 爽,李国和
(铁道第三勘察设计院集团有限公司地质路基设计处,天津 300143)
随着煤炭资源的不断采出,地下遗留了大量的“老采空区”[1],这些“老采空区”长期处于无人监测、无人管理的状态,其中,部分“老采空区”已延伸至建筑物下、水体下、铁路下,但由于缺少观测数据和有效的预计手段,对这些“老采空区”的勘察、评价、治理一直无计可施,致使采空区上工程的设计、施工缺乏依据,存在隐患。以往的研究多以终采时间、时间影响参数和深厚比作为重要的技术指标,忽视了对采空区移动过程和变形机理的推断,因此至今未找到好的切入点和预计方法。
1 采空区变形过程
采空区的变形是由“点”及“面”再到“体”的过程,其中“点”指采出的介质小单元,“面”指各个小单元采出后累积影响到覆岩及地面的表现,“体”指由垮落体、采空区边界悬臂梁(板)和平衡拱等共同构成的矿山压力平衡体系。与蠕变不同,其为“波动性缓沉”。
一般将采空区的变形过程分为2个阶段,即集中移动期(包括初始期、活跃期和衰退期)[2]和残余变形期[3,1]。集中移动期是指从地表累计下沉10 mm开始,至连续6个月地表下沉值累计不超过30 mm结束的这段时间[2]。采空区的绝大部分变形量发生在这个时期,变形后处于初始稳定状态。地表残余变形是指地表连续6个月累计下沉不大于30 mm后地表移动变形过程的延续[2],且6个月内地表最大下沉速度小于1.7 mm/d。与集中移动期比较,残余变形阶段地表移动不仅速度缓慢、变形轻微,机理也更为复杂。国内外对残余移动变形实测数据很少,研究也不够深入,因此残余移动变形计算尚没有成熟的方法。
由集中移动期和残余变形期的定义可知,2个变形阶段的划分是以一段时间内累计的下沉值为界限,并没有从覆岩移动机理的角度来界定,因此通常所说的残余变形量实际为“剩余变形量”。若假设整个变形期的下沉量为W,集中移动期的下沉量为Wh,残余变形期的下沉量为Wc,则下式恒成立
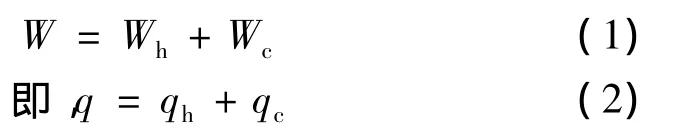
式中 q——整个变形期的下沉系数;
qh——集中移动期的下沉系数;
qc——残余变形期的下沉系数。
2 残余变形机理
地下开采结束以后,采空区在经过集中移动期后,在长时间的自然压实下,岩体受垮落体、采空区边界悬臂梁和平衡拱的支撑作用为静定结构(弯曲带为超静定结构)。因此,变形过程的延续需具备2个必要条件:(1)地面下有延续变形的空间量;(2)更改静定结构的约束。
2.1 残余变形空间量的来源
以往研究表明,采动破坏后的老采空区及其上覆地层的岩体呈“三带”分布[3],垮落带(相当于直接顶)呈碎裂状结构和散体状结构;断裂带(也称裂隙带,包括老顶,但不一定全部属于老顶)呈镶嵌碎裂状结构;弯曲带(也称缓沉带,对采场矿压无明显的影响)呈层状结构[4-6]。采空区内部岩体结构见图1。
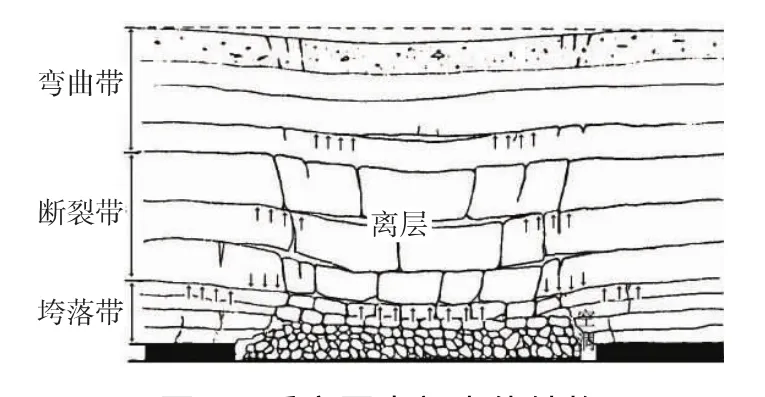
图1 采空区内部岩体结构
垮落带内的岩块具有显著碎胀性[7,8],根据我国一些矿区的测定结果,垮落岩块在初次采动及未承受其上覆岩层压力的自由堆积状态时,其碎胀系数为1.10~1.99,平均为1.40~1.62,具有显著的可压缩性。
在非充分采动条件下,位于整体弯沉带与导水裂缝带之间存在大量的产生于平衡拱之内的离层,最大的离层可达0.2~0.4 m[7](多存在于倾角较大,下薄上厚的覆岩条件下)。
据以往钻孔资料及模拟实验反映,采空区边界悬臂梁与垮落岩块间存在残留空洞,这也是延续变形空间量的重要来源[9-11]。
2.2 残余变形的促发
初始稳定状态的更改主要有2个方面的因素。
(1)内因:垮落岩块和破碎岩体在地下水和空气作用下强度衰减,造成再次失稳和压密。
(2)外因:由于外力作用,造成采场上覆岩体结构再次失稳变形,这些外力主要是地震力、区域地质构造活动引起的构造应力、附近采动或爆破造成的扰动作用力、地面附加荷载作用等。其中,除采动影响和地面附加荷载可大概推断控制外,其余外因作用的影响程度均具有不可预知性。
采空区在上述一个或几个因素的影响下,均会产生空洞的填充、垮落岩块再压密和离层压实,变形不断增大从而波及地表,在时间和空间上具有很多不确定因素[12-17]。
3 活化系数与充分沉降的关系
采空区达到初始稳定状态后,当煤层群开采(或厚煤层分层开采)时,若下层煤开采的影响超过上层煤开采时已经移动的覆岩,则地表受下层煤开采的重复采动影响发生二次下沉。二次下沉量并不是由下层采空区产生,而是老采空区在重复采动条件下的活化,二次下沉量与原下沉量的比值称为活化系数,由《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》(2000)给出(表1)。
由表1可知,覆岩受四次及四次以上重采扰动时的活化系数为0,即当受三次扰动移动稳定后,采空区不再移动,地表达到充分沉降。分别设三次重采下沉值和下沉系数为 W3、q3,则 W=W3、q=q3。

表1 按覆岩性质区分的重复采动下沉活化系数
4 残余变形下沉值
式(2)中,集中移动期的下沉系数qh一般可用地表移动变形实际观测结果求得,而由于q=q3,则q可根据《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》(2000)中的覆岩综合评价系数P及地质、开采技术条件来确定

式中 mi——覆岩i分层的法线厚度,m;
Qi——覆岩i分层的岩性评价系数。
三次重采分层岩性评价系数Q3与覆岩层单轴抗压强度R存在函数关系Q3=f(R)(图2),经推导得


图2 三次重采分层岩性评价系数与覆岩层单轴抗压强度函数关系
由式(2)得qc=q-qh,再利用概率积分法便可求出残余变形下沉值。
5 结语
(1)在深入研究采空区变形过程的基础上,提出“波动性缓沉”的概念。
(2)通过研究残余变形的机理,总结了初始稳定后延续变形的条件,并提出这个过程在时间和空间上的不确定性,因此下沉值与时间无直接的函数关系。
(3)以重复采动影响老采空区活化为切入点,提出“充分沉降”的概念,推导出计算残余变形下沉量的分段函数关系式。
[1] 张永波.老采空区建筑地基稳定性及其变形破坏规律的研究[D].太原:太原理工大学,2005.
[2] 国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[S].北京:煤炭工业出版社,2000.
[3] 何国清,杨伦,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991.
[4] 国家技术监督局,中华人民共和国建设部.GB 50218—94 工程岩体分级标准[S].北京:建设部标准定额研究所,1994.
[5] 中华人民共和国铁道部.TB10012—2007 铁路工程地质勘察规范[S].北京:中国铁道出版社,2007.
[6] 姜福兴.矿山压力与岩层控制[M].北京:煤炭工业出版社,2004.
[7] 范学理,刘文生,赵德深,等.中国东北煤矿区开采损害防护理论与实践[M].北京:煤炭工业出版社,1998.
[8] 王正帅.老采空区残余沉降非线性预测理论及应用研究[D].徐州:中国矿业大学,2011.
[9] 郭广礼,等.深部老采区残余沉降预计方法及其应用[J].阜新:辽宁工程技术大学学报(自然科学版),2002(1).
[10]王明立,张华兴.采煤沉陷区地表残余移动变形的计算分析[C]∥2005年开采沉陷规律与“三下”采煤学术会议.北京:2005.
[11]铁道第三勘察设计院集团有限公司.新建铁路沈阳至丹东客运专线DK53+200~DK67+200段受地下煤层采空区影响评价报告[R].天津:铁道第三勘察设计院集团有限公司,2010.
[12]杨逾,刘文生,冯国才.地下水位下降对采矿覆岩下沉影响探析[J].中国地质灾害与防治学报,2004,15(2):67-70.
[13]丁陈建.采动场地残余变形特征及预测模型研究[D].徐州:中国矿业大学,2009.
[14]郭高川,等.采空区残余地表移动变形对建筑物影响的探讨[J].煤炭工程,2008(5):72-74.
[15]白国良,李树志,高均海.老采动区覆岩裂隙发育特征及活化机理研究[J].煤矿开采,2010,15(5):11-13.
[16]张宏贞,邓喀中,谭志祥.老采空区残余移动变形分区研究[J].矿山压力与顶板控制,2005(2):32-34.
[17]刘辉,马金荣.煤矿废弃老采空区地表残余变形计算[J].山东煤炭科技,2011(5):73-74.

