基于高斯混合模型的林业信息文本分类算法

陈 宇，许莉薇

（东北林业大学 信息与计算机工程学院，黑龙江 哈尔滨 150040 ）

基于高斯混合模型的林业信息文本分类算法

陈 宇，许莉薇

（东北林业大学 信息与计算机工程学院，黑龙江 哈尔滨 150040 ）

为解决传统林业信息文本分类算法准确率低和正确率分布不均匀的问题，提出了一种基于高斯混合模型的林业信息文本分类算法。在阐述高斯混合模型和EM算法的基础上，使用TF-IDF方法计算林业信息文本特征值，对构造的林业信息文本特征矩阵降维，结合Kmeans算法，通过训练得到各类林业信息文本所对应的高斯混合模型的参数，构造分类器进行精准与快速分类。实验结果表明，该算法与神经网络分类方法、贝叶斯、决策树等常用分类算法相比，该算法有较高的准确率和实用性，为林业信息文本的分类研究开拓了新思路。

林业信息；文本分类；高斯混合模型；参数估计

文本分类是根据建立好的分类器，让计算机对给定文本集进行分类的过程[1]。文本分类的原理主要是通过建立文本分类器，选择有代表性的特征与未知样本比较相似度，将未知文本划分至最相似的一类文本中。文本分类的过程包括：文本预处理，文本向量表示，构造分类器，分类结果评价。

国外对文本分类技术的研究起步较早，并且现阶段发展也比较完善。常用的文本分类算法包括K邻近算法、贝叶斯算法、决策树[2]、神经网络算法[3]等。

我国对文本分类算法的研究起步较晚，初期我国主要对国外技术总结，随后是对传统算法的优化改进，扩大了文本特征的选择的范围，随着文本分类技术的进步，现阶段我国文本分类技术发展的也较好，研究出许多适合文本分类的算法，但是仍存在一些缺陷，在实际应用时因为训练样本存在差异，所以使得分类算法对分类结果差异较大，因此本研究研究的重点就是如何提高对不同类文本分类的准确率和效率。

现阶段对于林业信息文本分类的研究甚少，因此如何提高林业信息文本分类的正确率，是一个重要的研究内容。

近年来高斯混合模型引起广泛关注，高斯混合模型是一种常用的描述混合密度分布的模型，是多个高斯分布的混合分布。在分类问题的学习中，能够有效地体现类内数据在特征空间中的分布特点。近年来，高斯混合模型在语音识别、人脸识别和图像处理等方面有很好的应用，但将其应用在林业信息文本分类领域的研究甚少。由于高斯混合模型理论比较成熟，且能拟合任何形式的分布，因此在林业信息文本分类领域也应该具有较好的发展前景。

本研究提出了一种基于高斯混合模型的林业信息文本分类算法。首先，利用中科院分词系统对不均衡林业信息文本进行预处理；其次，使使用经典的TF-IDF公式计算文本分词的特征值，构成特征矩阵[4]；然后，对特征矩阵降维；最后，构造高斯混合模型分类器（使用参数估计算法结合Kmeans算法得到模型的初始参数ak、μk、Σk的值，建立分类器），以达到分类的目的。通过大量实验论证该算法已达到预期目的，有较高的分类正确率，并且准确率明显高于BP、决策树、贝叶斯分类方法，为林业信息文本分类提供了新方法。

1 关键技术

林业信息文本表示

假设所有不均衡林业信息文本有n个特征,形成n维的向量空间，每个林业信息文本d被表示成n维的特征向量：

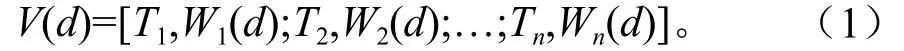
Ti为n个分词中的一个，Wi(d)为Ti在文本d中的权值, 文本分词的权值通过TF-IDF公式计算[5]：

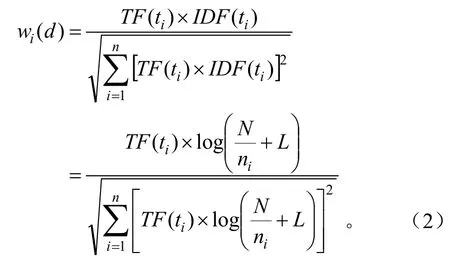
式(2)中，Wi(d)是计算出的特征词Ti的权值，TF(ti)是特征词Ti在d中出现的次数，N指样本总个数，ni为出现了Ti的林业信息样本的个数。

林业信息文本特征选择

设n个样本，样本有p项指标[6]：X1，X2，…，Xp，得到初始特征矩阵为[4]：

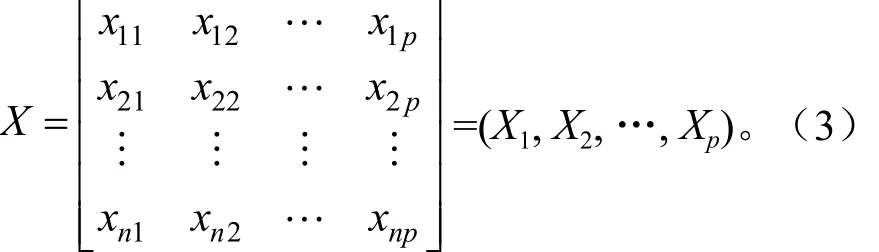
其中：

综合指标向量X是p个向量X1，X2，…，Xp作线性组合：

可简写为：

系数ai=(a1i，a2i，…，api)的限制条件：

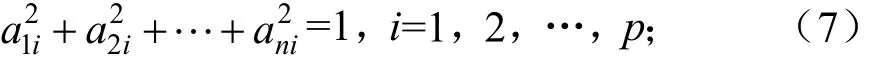
特征矩阵的协方差矩阵是S=(Sij)p×p其中：

计算S的特征值λ1≥λ2≥…≥λn＞0与对应单位向量：

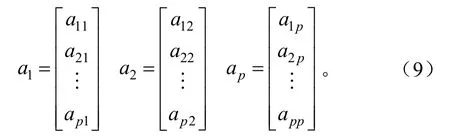
X的第i个主成分为Fi=a′iX，i=1，2，…，p

主成分的确定根据贡献率ai和累积贡献率G(r)：

实验中，选择累积贡献率达到99%的主成分，n个文本在所选r个主成分的得分：

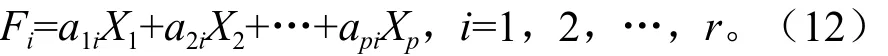
林业信息文本分类算法

林业信息文本分类常用的方法有BP、贝叶斯、决策树等，这些方法受到林业信息样本影响较大，因此不同样本分类的正确率差异大，高斯混合模型实验得到了较好的效果，分类结果精准并且正确率分布均匀。

高斯混合模型是一种常用的描述混合密度函数分布的模型，矢量特征在概率空间的分布状况通过若干个高斯概率密度函数的加权和进行描述。即每个高斯混合模型是由K个Gaussian分布构成，一个Guassian是“Component”，形成多个分类器，对Component进行线性加和形成混合高斯模型的概率密度函数[7]：

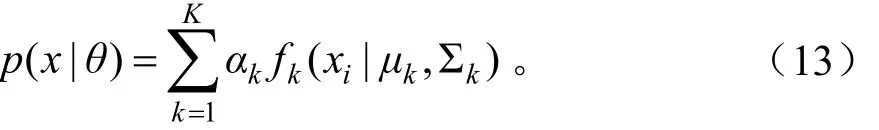
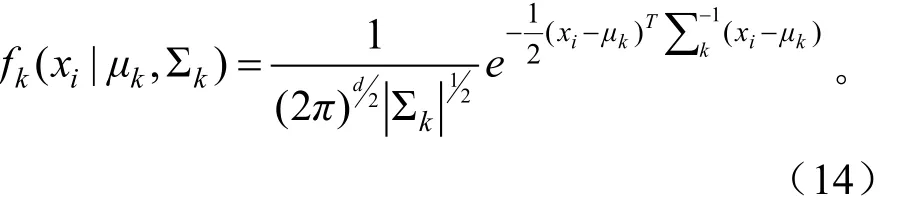
在式（14）中，μk是均值，Σk是协方差矩阵。

GMM模型的各个分量是通过均值和方差表示的，GMM的分类过程，是以均值为中心的椭圆体分布，方差决定它的几何性质。使用高斯混合模型对林业信息文本分类，首先对未知参数K、ak、μk、Σk的值进行初始化，才能构造GMM模型，对概率密度函数建模。林业信息文本的样本是五类，分为土壤类、花类、树木类、虫类、水类。因此参数K=5，对于剩余3个参数的估计有多种方法，使用的比较频繁的是EM算法。

EM算法也称作期望最大算法，是对参数的最大似然估计，此算法主要应用在如下方面：其一是对不完整数据的估计，其二是假设缺失的数据存在，降低似然函数复杂度[8]。

EM算法的执行过程[9]：

首先：计算期望（Expectation），估计隐含变量。观测数据确定，对完整似然函数的期望计算。

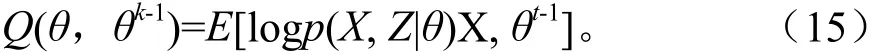
其中，θk-1是当前的参数估计值，θ是更新后的参数值。

然后：计算极大值，对其他参数估计。

求解θ，使Q(θ，θk-1)得到极大值，即

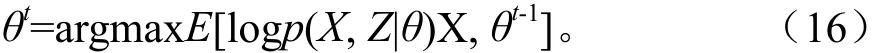
在高斯混合模型中，样本数据由不完整数据构成，则加入隐含变量Z={z1，z2，…，zN}，zi={zi1，zi2，…，zik}独立分布于K类，隐含变量的概率分别为α1，…，αk。满足如下，

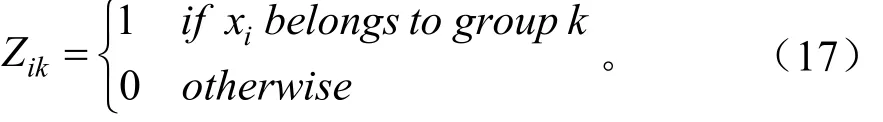
算法执行过程中对数似然函数定义为：

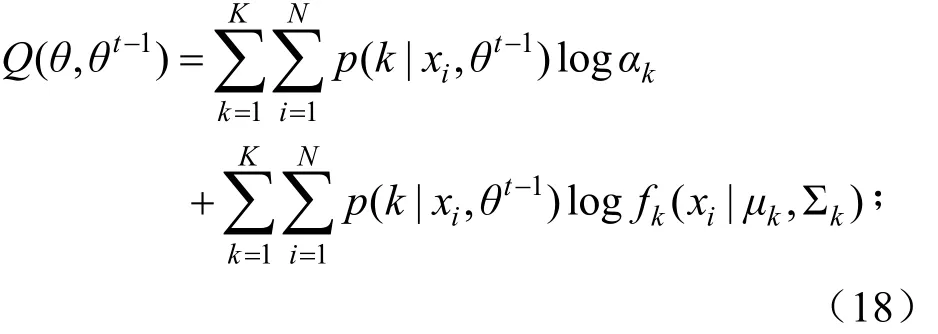
上式p(k|xi，θt-1)是K类分布的后验概率：

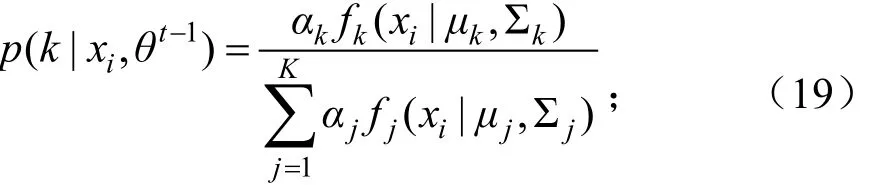
使用梯度法求解条件极值，可得如下关系：

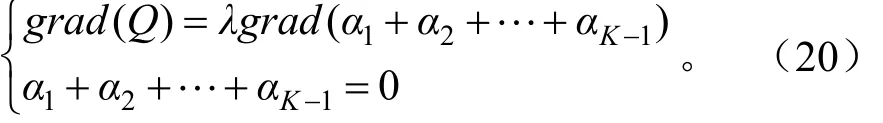
即

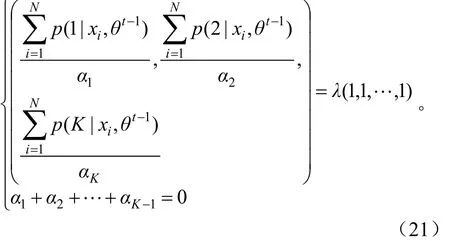
其中

对Q(θ，θk-1)求其关于μk、Σk的导数，让其为0可得均值重估公式：

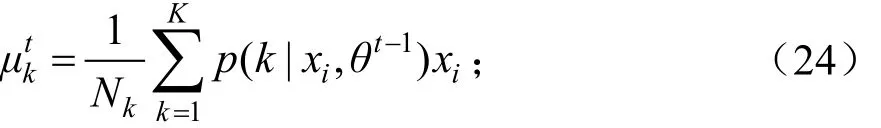
方差重估公式：

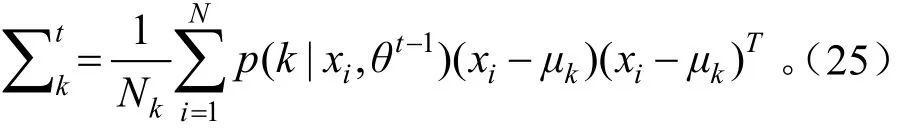
迭代终止的条件就是迭代重估公式，直到满足预先设定的条件。EM算法涉及的理论比较简单和单一，其主要优点是简单和稳定，每次迭代都能保证观察数据对数似然是增大的，但EM算法也有其缺点，主要是收敛速度慢，尤其当输入的数据维数过高或者规模过大时，将严重影响收敛速度。EM算法能找到局部最大点，但对于找全局最大点比较困难[10]。EM算法的初始化有严格的要求，对于不同的初始值，能够使得结果又较大差异[11]。目前最有效的方法是将Kmeans算法与EM算法相结合，使用Kmeans算法来计算群聚中心点，当做EM参数中均值的初始输入值。

Kmeans聚类是聚类算法中常用的算法[12]。该算法输入参数K，对输入特征矩阵划分为K个聚类，相同聚类对象的相似度较高，反之较小。主要思想是：选取K个中心点聚类，对最靠近中心点的对象归类，通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果[13]。得到各个聚类的中心点之后，将其作为EM算法初始值，该算法使用的很广泛，尤其是和EM算法相结合，先对初始数据进行粗略分类，再将得到的数据作为参数估计初始化的数据。将这两种算法结合能能提高EM算法收敛的速度和分类的正确率。

2 实验结果

实验初步针对林业信息文本样本进行选择，如表1所示：

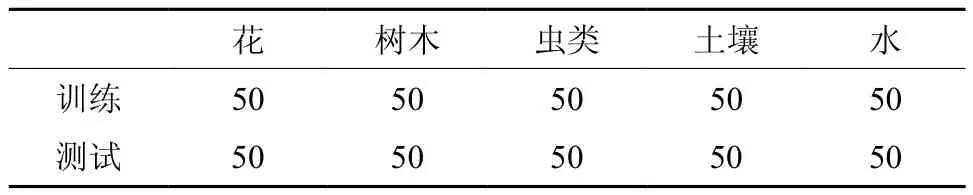
表 1 实验样本选择个数Table 1 Selection numbers of experimental sample

表1所示，选取林业信息的5个类别：花、树木、虫、土壤、水，训练样本和测试样本是每个类别选取50个，测试样本是对原训练样本数据加高斯白噪声产生，样本总共500个。

先对样本进行预处理，使用经典的TF-IDF方法计算文本特征词的权值，构成训练样本的初始特征值矩阵，对训练样本的初始特征矩阵加高斯白噪声形成测试样本初始特征矩阵，由于训练和测试样本初始特征矩阵维数过大会影响算法执行效率，并且在使用有些算法时容易造成过拟合现象，所以对文本初始特征矩阵降维，得到新的特征矩阵，再进行分类操作。如下图1所示为高斯混合模型的林业信息文本分类的流程图：

训练和测试样本初始特征矩阵维数均为250×1127维，降维后形成新的特征矩阵维数均为250×213维，文本类别总数K=5，先利用Kmeans算法求解样本数据中心，即EM算法所需的初始值，然后通过对EM算法的初始化，构造高斯混合模型，计算出初始值为α=[0.2，0.2，0.2，0.2，0.2]，μk为213×5维的数据，Σk规模为213×213×5，将以上参数带入，可得到高斯混合模型结构为：

图1 构造GMM分类器的流程Fig.1 Technological process of constructing GMM classif i er

通过式（26）对测试样本分类，将每个降维后的测试文本特征矩阵带入到地f1、f2、f3、f4、f5中，比较其的大小，这5个分量分别代表5个类别，因此哪个分量的值越大，则说明该测试样本属于该类别的概率越大，对所有的样本进行此项操作，每次都选出数值最大的分量，该分量就代表着测试样本类别。

使用BP、决策树、Bayesian、GMM四种方法分类，选取相同的样本，每类样本各50个，总共250个测试样本，测试结果如图2所示，横坐标是测试样本数目，纵坐标是分类器分类的正确率。

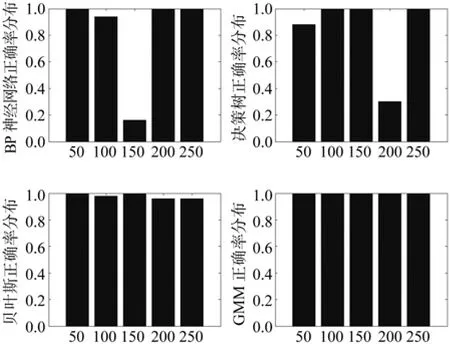
图2 分类算法正确率分布Fig.2 Distribution of classif i cation algorithm accuracy

在图2中，能够分别看出4种分类方法在处理不同类别文本时分类的正确率，BP神经网络对林业信息文本分类时不够稳定[14]，对于虫类文本的识别率很低，决策树分类方法对林业信息文本分类时也不够稳定，对于土壤类文本分类正确率很低，贝叶斯和高斯混合模型在处理林业信息文本时相对稳定，但是GMM模型分类算法的正确率高于决策树分类算法。

图3是4种分类方法随着文本数目的增加所显示的分类正确率，横坐标为林业信息文本的测试样本数目，纵坐标为分类器分类的正确率。本实验5类文本随机各选取5个样本，共25个样本，图中可看出每种分类算法的分类正确率的转折点，以及4种分类方法是在第几个文本样本判断时出错。实验数据对比可得4种分类算法中GMM模型分类性能较高。

图3 分类器分类结果对比表示Fig.3 Contrast of classif i cation results

使用250个林业信息测试样本，4种分类方法正确率对比图，图4中能看出每个分类器的分类效果，横坐标是林业信息文本测试样本的数目，纵坐标是分类的正确率。

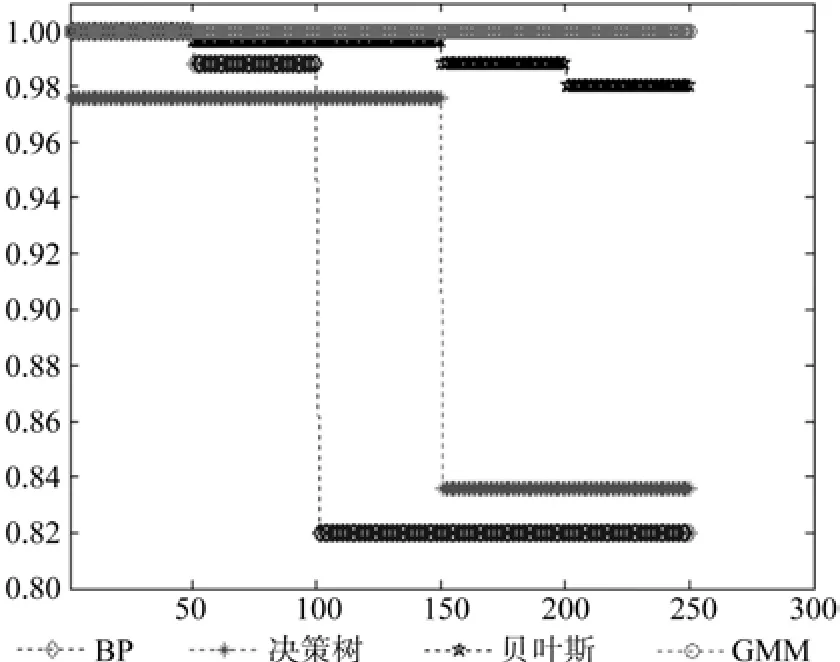
图4 分类器分类总结果对比Fig.4 Comparison of classif i cation results

4种分类器实验采用相同的训练样本与测试样本，主要使用了BP神经网络、决策树、贝叶斯这3种方法与高斯混合模型分类算法作对比，这四种算法实验结果如表2所示：

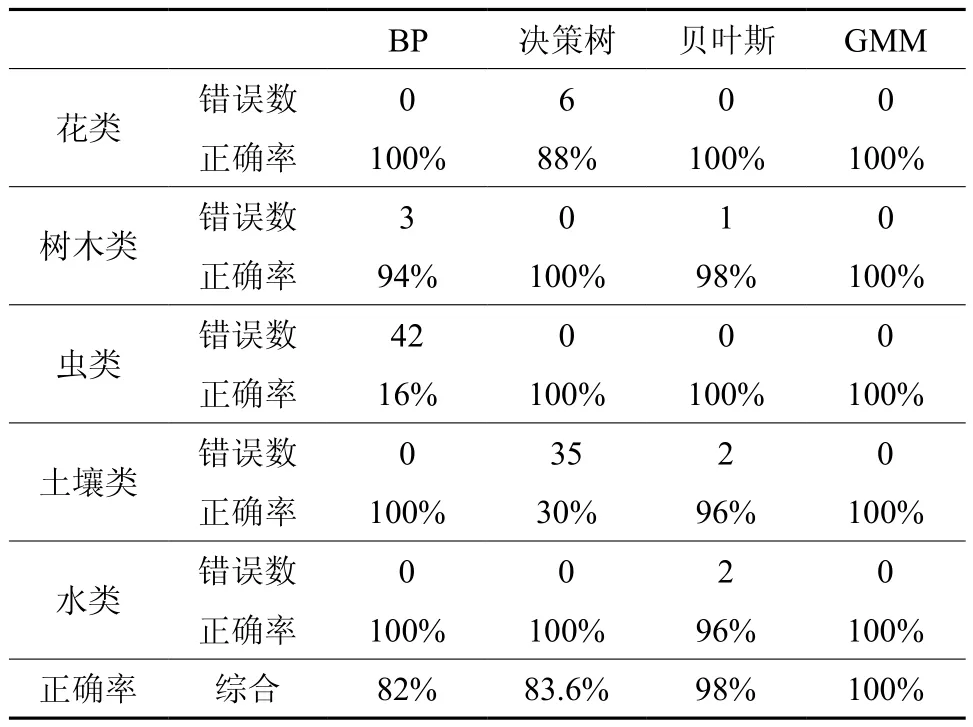
表2 林业信息文本分类算法结果比较Table 2 Comparison of forestry information text classification algorithm

通过实验结果可知，本研究提出的基于高斯混合模型的林业信息文本分类算法能够实现对5类林业信息文本精准与快速的分类，分类效果明显优于神经网络、决策树、贝叶斯分类算法；分类正确率均匀分布，每类文本都能正确分类，分类能力较强。

3 结束语

基于GMM模型的林业信息文本分类算法，使用权值计算公式TF-IDF计算权值后对初始特征矩阵降维，构造林业信息文本的特征矩阵，来反应文本的特征。结合EM算法估计参数并通过Kmeans得到初始参数，建立GMM模型。通过实验表明，GMM算法适用于林业信息文本的分类，分类正确率高于分类算法神经网络、决策树、贝叶斯，为林业信息文本分类开拓了新思路，有较高的实用价值。

[1] 张 浩,汪 楠. 文本分类技术研究进展[J].计算机与信息技术, 2007,23(1):95-96.

[2] 陈 利,林 辉,孙 华,等. 基于决策树分类的森林信息提取研究[J].中南林业科技大学学报, 2013,33(01):46-51.

[3] 李永亮,林 辉,孙 华，等. 基于BP神经网络的森林树种分类研究[J].中南林业科技大学学报, 2010,30(11):43-46.

[4] 章 兰. 一种基于VSM模型的动态文本分类器的设计[D].苏州：苏州大学,2004.

[5] 段江丽. 基于SVM的文本分类系统中特征选择与权重计算算法的研究[D].太原:太原理工大学,2011.

[6] 王雅菲. 文本分类中特征降维方法的研究[D].长春：长春工业大学, 2010.

[7] 岳 佳,王士同. 高斯混合模型聚类中EM算法及初始化的研究[J].微计算机信息,2006,11(3):244-246.

[8] A P Dempster, N M laired, D B Rubi n. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society, 1977,B(39):1-38.

[9] 岳 佳,王士同. 双重高斯模型的EM算法的聚类问题研究[J].计算机仿真,2007,24(11):110-113.

[10] 曹红丽.混合高斯模型的混合EM算法研究及聚类应用[D].乌鲁木齐：新疆大学,2010.

[11] Jinwen Ma,Shuqun Fu. On the correct convergence of the EM algorithm for Gaussian mixtures[J]. Pattern Recognition, 38(12):2602-2611.

[12] Jamshidian M, Jennrich R I. Conjugate gradient acceleration of the EM algorithm[J]. Journal of the American Statistical Association, 1993, 88:221- 228.

[13] Jie Cao, Zhang Wu, Junjie Wu, Wenjie Liu. Towards informationtheoretic K-means clustering for image indexing[J]. Signal Processing, 2012.

[14] 杨新武,李 森,刘椿年. 基于BP网络的中文文本分类技术[J].微计算机应用,2008,29(3):1-6.

Forestry information text classif i cation algorithm based on GMM model

CHEN Yu, XU Li-wei
(School of Information and Computer Science, Northeast Forestry University, Harbin 150040, Heilongjiang, China)

In order to solve the problems of low categorization accuracy and uneven distribution of the traditional forestry information text classif i cation algorithm, a forestry information text classif i cation algorithm based on Gaussian mixture model (GMM) was puts forward. On the basis of Gaussian mixture model (GMM) and the principle of parametric estimation algorithm, the formula of TFIDF was used to compute text eigenvalue, the constructed feature matrix of forestry information text was reduced in the dimension of eigenmatrix. The Kmeans algorithm should be used, then get the parameters of Gaussian mixture model (GMM) through training of forestry information text, lastly a classif i er of Gaussian mixture model (GMM) was established to achieve the goal of faster and accurate classif i cation of forestry information text. The experimental results show that the algorithm has higher accuracy and practicality than the algorithm of neural network and Bayesian and decision tree, and the algorithm pioneer new ideas for studying the forestry information text classif i cation algorithm.

forestry information；text classif i cation; Gaussian mixture model; parametric estimation

S711

A

1673-923X(2014)08-0114-06

2013-09-02

国家948项目(2011-4-04)；中央高校基本科研业务费专项资金项目(DL12CB02)；黑龙江省教育厅科学技术研究项目(12513016)；黑龙江省博士后基金；黑龙江省自然科学基金项目(F201347)；哈尔滨市科技创新人才专项资金项目(2013RFQXJ100)

陈 宇（1975-），男，黑龙江哈尔滨人，博士后，副教授，研究方向为数学物理反问题求解，探测与成像，图像处理

[本文编校：文凤鸣]