金融时间序列中同积向量的充分改进最小二乘估计研究
曹 潇
(西北政法大学 经济管理学院,西安710100)
在金融资产价格波动研究中,同积过程{yt}的同积向量往往是未知的,需由观察到的样本估计得到。现有文献对同积向量的最小二乘估计、估计量的极限分布和对同积向量的假设检验进行了研究[1-3],但是没有考虑矩阵∑21不为零时的情形,统计量T(^γT-γ)的极限分布是非标准的。本文将研究同积向量的充分改进的最小二乘估计方法,旨在克服这一困难。这一研究可以为实际的微观金融资产波动分析提供有力的工具。
1 同积向量的最小二乘估计
若n维随机向量同积,并有同积向量a,那么a可由最小二乘法一致地估计得到。为说明最小二乘法的合理性,作以下考虑。a为yt的同积向量,因此zt=a′yt为一单变量I(0)的过程。
但是,若a不是yt的同积向量,那么zt=a′yt仍为I(1)变量,此时可得
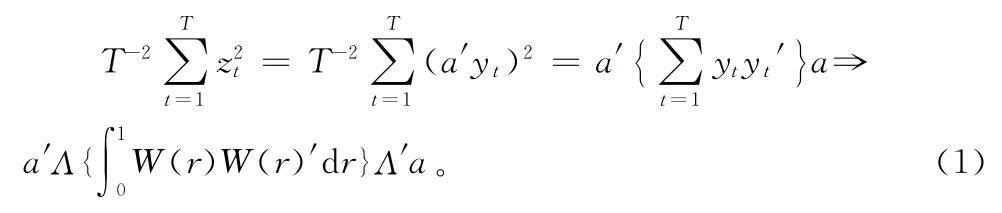
式(1)中,T为样本量,W(r)是标准维纳过程,r∈ [0,1]。令Λ=Ψ(1)P,Ψ(L)为无穷阶滞后多项式,Λ决定于Δyt的自相关系数矩阵。(1)式是一正定的二次型,从而有
因此,只要yt是同积的,并有同积向量a,以下最优问题
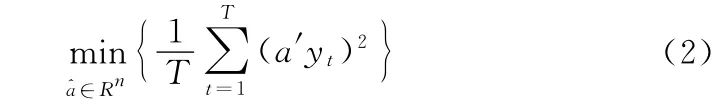
的解a,即A的最小二乘估计,是同积向量的一致估计。

同积向量的最小估计通常在同积过程的三角表示形式中进行。同积过程{yt}的三角表示形式为:
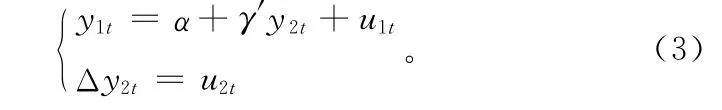
这里,y1t为单变量随机变量,y2t为(n-1)维随机向量。现有文献给出了参数α和γ的最小二乘估计。
2 充分改进的最小二乘估计
同积向量的充分改进的最小二乘估计(fully modified OLS),简称改进的OLS。考虑同积系统的三角表示形式:
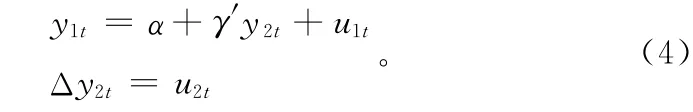
(u1t,u2t)′有表示形式= Ψ(L)ε,其中,Ψ(L)为无穷阶滞后多项式,{εt}独立同分布,E(εt)=0,D(εt)=E)= Ω=PP′。令Λ = Ψ(1)P,则有:
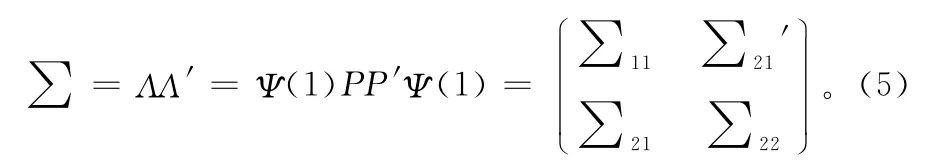
若∑21不为零,构造将其从y1t中减去,可得修改后的同积系统为=α++,其中其中的矩阵L′对中的参数作估计,得最小二乘估计^α+T和^γ+T,
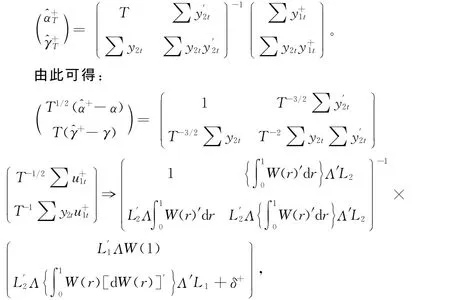
其中,W(r)为n维标准维纳过程,参数δ+的表示式:


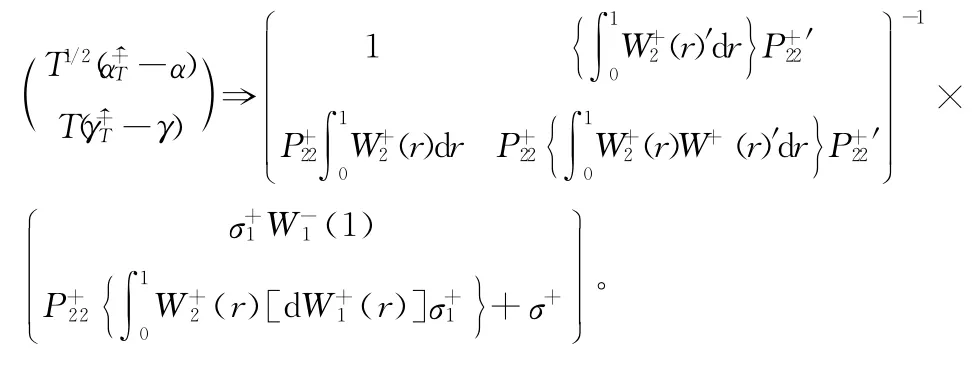
方差矩阵∑可由下式

3 结论
综上分析,构造充分改进的最小二乘估计^α++T和^γ++T需要采取以下步骤:先以y1t对常数和y2t作回归,取得残差^u1t;然后用^u1t和^u2t构造估计量^Γv和;对y1t作调整=计算^δ+;最后用对常数和y2t作回归,并将 T^δ+从(∑y2t^y+1t)中减去。
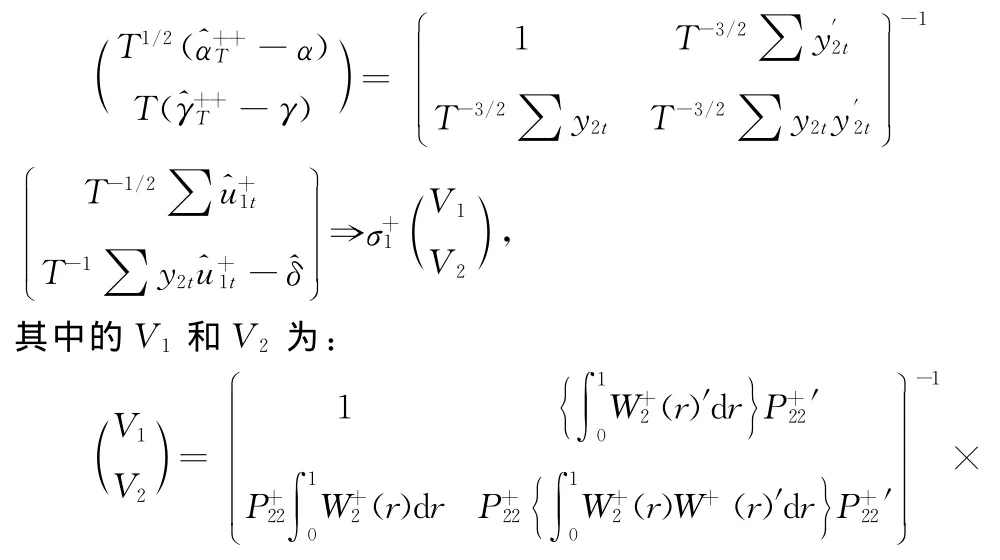

值得注意的是,以上的分析并不依赖于u1t和u2t的具体的参数结构,所以从这个意义上说,改进的OLS方法是一种非参数的方法,有助于充分的最小二乘估计。
[1] 王志强.基于改进最小二乘支持向量机的最优解估计方法[J].计算机与应用,2013(11):27-28.
[2] 程延强.广义均方误差标准下双类估计优于最小二乘估计的充分条件[J].中国科教创新导刊,2008(10):21-23.
[3] 杨旸.相依误差下线性回归模型最小二乘估计的相合性[J].统计与决策,2014(4):31-33.
[4] 陈海清.广义Pareto分布参数的最小二乘估计[J].应用概率统计,2013(4):64-70.
[5] 尹小红.线性模型广义最小二乘估计的中偏差、重对数律与相对效率[J].湖南文理学院学报:自然科学版,2013(3):27-28.

