弹载相控阵卫星跟踪系统设计与测角研究
李朝海,姜雯献,王国龙,董 涛
(1.电子科技大学电子工程学院, 成都611731; 2.航天恒星科技有限公司, 北京100086)
0 引言
在各类卫星通信系统中,由于载体在运动过程中,姿态和地理位置发生变化,会使天线的指向偏离卫星,造成通信中断。为了能达到最佳通信效果,必须对载体的这些变化进行隔离,使天线始终对准卫星。
自跟踪接收系统将天线馈源处接收到的射频微弱信号放大、变频、滤波及角误差(包括方位误差和俯仰误差)检测,并把角误差信号传入跟踪滤波器,通过稳健的跟踪滤波算法实现对卫星目标位置的准确预测,控制天线波束对准目标信号[1],实现对目标信号的自动跟踪,最终使双向微波综合信道达到最佳的通信效果。
1 系统方案
如图1所示,天线波束自跟踪系统架构设计,采用单脉冲跟踪方式[2],利用接收阵列接收到的信号完成对通信卫星的连续跟踪,并控制发射波束自动指向卫星方向。图中(φ,θ,φ)分别代表载体方位角、俯仰角和横滚角。

图1 天线波束自跟踪系统架构图
为实现基于相位比较的单脉冲跟踪,需将接收阵列划分成若干个子阵,这里按最小子阵数设计,划分成4个2×4的子阵。各天线单元的信号合成4个子阵,进行4路模数(A/D)变换,得到的基带数字信号在接收信号处理部分形成和波束,得到的和波束接收信号通过信号输出端,送给解调、解码分系统。同时,在图1中的接收信号处理部分采用比相法提取出角度误差信息,送入数字波束定向系统进行跟踪滤波运算,得到波束指向控制的跟踪滤波结果,处理过程中将利用运动平台主机送达的平台姿态角信息,完成单脉冲闭环跟踪处理,实时调整收发阵列波束指向,确保收发天线波束一直对准卫星方向。
2 相控阵卫星自跟踪系统关键技术
2.1 角度搜索/捕获过程
运动平台设备获得的卫星位置预报信息和平台姿态的测量结果难免存在一定的误差,它使得自跟踪系统不能直接转入闭环跟踪状态,而需经过搜索/捕获阶段。
搜索/捕获的方案设计如图2所示。数字天线波束自定位(DAPS)系统根据卫星在惯性空间的初始位置信息,给出波束在惯性空间的搜索方向指向(实际中为惯性空间方向余弦参数),利用平台姿态数据将波束指向信息转换为平台和天线坐标系下的波束指向,实现对搜索波束的指向控制。
对每一个驻留波位,DAPS系统首先进行4通道接收,利用子阵间的信号互相关进行信号检测,若超过检测门限,则利用下面介绍的顺序多波位方法实现方向捕获,来波方向经捕获过程确定后,在来波方向形成接收和波束,对信号进行解扩、解调等,以确认接收的信号是期望的协作通信信号,然后转入跟踪模式;否则进入下一个波位重新搜索。
根据要求,DAPS系统能采用程序跟踪和自跟踪的方式捕获并稳定跟踪中继卫星,二者之间的主要差别是搜索的角度范围不一样。
8个阵元的半波长均匀等间隔线性阵列的波束宽度约为13°,如果极限情况下平台姿态测量误差的均方根为5°,则其4倍的方差为20°,其范围已经远大于单个波束的宽度。此时,需要根据不同的情况设计不同的捕获方式。
姿态测量精度比较高的时候,将采用程序跟踪方式,可以确定目标位于预测的波位范围之内。为保险起见,使用图3所示排列的顺序多个波位完成卫星信号的方向捕获。
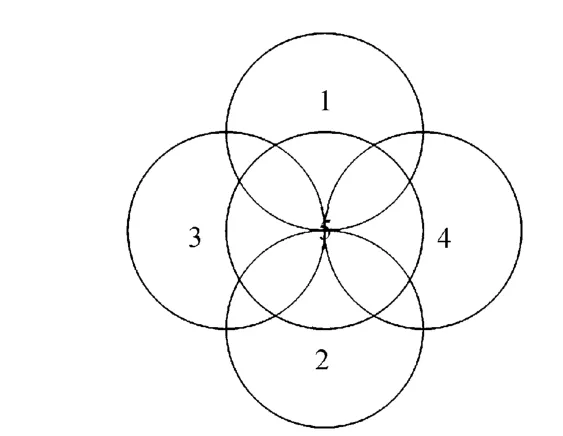
图3 截获状态1波位排列
比较4个波位内输出信号的幅度,判断目标更靠近哪一个波位的中心,并用类单脉冲方法处理,以最终确保波位5的中心逐步对准信源方向,满足转入单波位比相跟踪的条件。如果姿态测量精度较差,则用更大的截获波位矩阵或者补充搜索实施对卫星信号的捕获(如图4中的状态2截获逻辑)。
综合考虑,捕获过程整体的处理逻辑如图4所示。

图4 跟踪系统角度捕获过程
无论是搜索状态还是截获2状态,只要任意一个波位检测出可信的通信信号,则截获过程直接转入截获状态1的顺序多波位类单脉冲捕获转跟踪过程。
捕获/确认过程的SNR和时间估算:
设波束在一个波位的驻留时间为5 ms(即跟踪时的更新周期),由于符号速率为3 kb/s,32阵元接收解扩后的Eb/N0为25 dB,5 ms内有15个符号,搜索时左右子阵(或上下子阵)阵元数为16个,两子阵信号的互相关SNR(近似)为

式中:25 dB为一个符号解扩后的Eb/N0;+3 dB是考虑匹配滤波后SNR=2Eb/N0;10lg(15)为15个符号积累;第一个-3 dB为子阵阵元数为32个(即64阵元的一半),第二个-3 dB为3 dB波束宽度。
SNR=33.7 dB,信号正确检测的概率大于99%。
搜索/捕获/确认过程的时间为

式中:SBP为1个搜索波位时间;SCP为1个顺序捕获波位时间;DCT为解扩解调确认时间。
式中的4倍,是考虑由于接收波束较宽,通常4个波位能完成搜索捕获过程,恶劣情况下可能适当增加。
2.2 角度跟踪过程
跟踪状态下,各模块之间控制与连接的逻辑关系如图5所示。图中εφ和εθ分别表示方位角误差和俯仰角误差。

图5 波束跟踪状态软硬件实现逻辑关系
接收阵列接收得到的信号经过A/D采样变成数字信号,经数字下变频、滤波、抽取过程,变成适宜于实时处理的数字信号,再经相关处理剔除噪声的影响,保留子阵之间的相位差信息。这些相位信息中包含了入射信源相对于接收阵列的角度信息,利用单脉冲比相方法就可以提取这些角度信息。
利用运动平台惯性设备传递过来的平台姿态数据,可以将阵面坐标系下的角度信息转化成惯性坐标下的角度信息。跟踪滤波器完成惯性坐标系下的角度跟踪,再将预测角信息转换到阵面坐标系下,用于控制接收阵列的波束指向,最终完成对入射信源的角度跟踪。
此时,角度预测信息还送至发射阵列,用于控制其波束对准卫星方向。
角跟踪系统还必须考虑姿态变化导致的信号闪烁甚至跟踪丢失问题,其处理流程如图6所示。
正常情况下,跟踪系统利用接收到的角误差信号完成跟踪滤波处理,利用角度预测信息控制收、发天线波束的指向。
如果接收到的信号出现闪烁现象或跟踪丢失,则跟踪系统利用回路的记忆功能外推若干周期,继续接收并跟踪预测方向的信号。外推超过限定的周期数时,可能跟踪回路已经失锁,此时应中断当前跟踪,重新转入搜索捕获逻辑[3]。

图6 角度跟踪/记忆处理逻辑
为实现上述处理逻辑,信号处理回送的信息中不仅只有角跟踪残差信息,还包括接收信号幅度等内容,据此可以判别当前周期采集信号是否正常。
2.3 接收工作过程时序设计
对波束自跟踪系统而言,接收信号处理、捕获与跟踪处理、波束控制这三个方面的工作属于相对独立的任务模块,三个任务之间又存在数据传递的需求关系,为此需要设计专门的协作时序[4]。
计算机或DSP系统多数按调度周期工作,考虑到数据采集和角度误差提取对信噪比的需求,选择5 ms~10 ms作为基本的调度和信号采集、处理周期。
与项目较为类似的雷达系统中,由于不同硬件或任务之间的数据信息传递制约关系,跟踪滤波器的采样周期一般只能取3个或3个以上的调度周期。
如图7所示,第n-1周期采集的信息在第n周期被处理后,在第n周期末(或第n+1周期初)就可以作出响应,实现对波束的指向控制。从图7看出,可以将跟踪滤波器的采样周期设置为调度周期的2倍。

图7 系统工作协调性设计
3 相控阵二维测角实验验证及仿真
3.1 测试坐标系定义
接收天线阵面及坐标示意图如图8所示,Z轴的垂直纸面向外。测试角度示意图如图9所示,俯仰角θ为来波方向与Z轴夹角,方位角φ为来波方向在XOY平面内投影与X轴的夹角,接收阵列安装在XOY平面内。
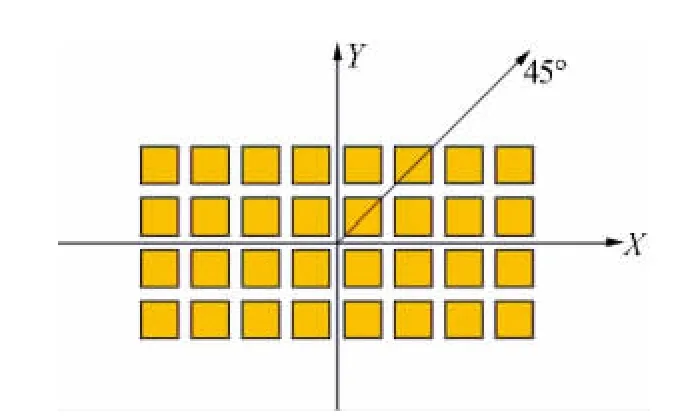
图8 接收天线阵面及坐标示意图
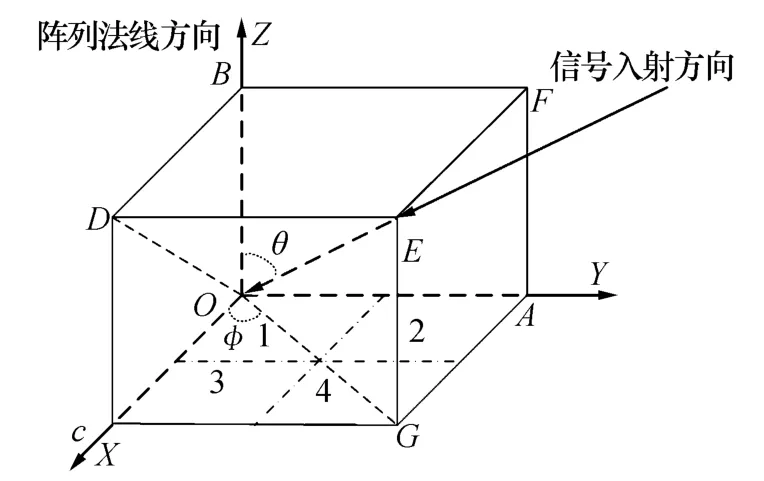
图9 测试角度坐标示意图
3.2 测试方案设计
在箱形微波暗室中进行实际测试验证,由于对测角精度进行精确的测试比较困难,通过差分方式进行测试,即对转台转动前后的角度差进行测试[5]。测试系统连接图如图10所示。
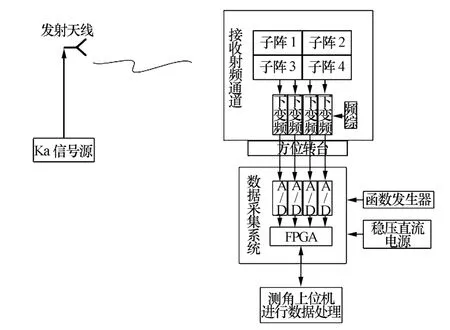
图10 测试系统连接图
测试系统主要分为4个部分:发射天线、接收射频部分、数据采集系统[6]、测角上位机。
由于发射天线位置固定,无法改变实际的来波方向。在实际的测量过程中,转台控制上位机完成对方位转台水平旋转的控制,将接收阵列垂直于转台平面放置。通过旋转水平转台,带动4个接收子阵进行旋转。接收阵列相对于来波方向的夹角发生变化,将接收阵列的旋转等效于来波方向的变化,完成对方位角和俯仰角的改变。由于实验条件受限,方位转台只能完成水平方向旋转,无法进行垂直方向旋转,所以在接收阵列安装时,需要注意阵面的安装方式,只有通过特定的安装方式才能实现方位角或俯仰角的变化。
接收阵面的安装方式分为两种:
(1)阵面X轴、Z轴与转台平面平行,Y轴与转台平面垂直
在此情况下,如图8和图9所示,使方位角φ=0°,来波方向控制在XOZ平面,通过旋转方位转台,就可以实现对俯仰角θ的改变。
(2)阵面Y轴、Z轴与转台平面平行,X轴与转台平面垂直
在此情况下,如图8和图9所示,使方位角 φ=90°,来波方向控制在YOZ平面,通过旋转方位转台,同样可以实现对俯仰角θ的改变。
通过波控上位机可以完成对接收阵列波束指向的控制。4个接收子阵对来波信号进行接收,通过下变频处理,将信号从射频搬移到中频,中频信号经过A/D完成采样,FPGA对A/D采样数据进行存储。测角上位机对实测数据进行读取,并保存在上位机,方便以后对实测数据的处理。
二维测角实验需要完成对实测数据的后期处理,对A/D采样之后的数字中频信号进行数字下变频处理,并进行相位信息的提取。经过数字下变频处理得到的4路复基带信号作为4个子天线阵接收到的信号分别记为 y1(n)、y2(n)、y3(n)和 y4(n)。
由图9可知,来波方向在3个坐标轴的方向余弦为=


一般来说,上式中的噪声功率可忽略,此时分别求出 Aφ3和 Aφ2的相位,需注意,此时 Aφ3和 Aφ2的相位Δφ3与Δφ2之间的关系为

把Δφ2和Δφ3分别代入式(7)、式(8),即可实现测角。vφ3和vφ2为输出噪声。理论上,只要积分时间足够长,可以得到较高精度的角度测量。
3.3 仿真结果及分析
(1)理想情况下测向精度随SNR变化情况
假设信号从(θ,φ)为(30°,50°)方向入射进来,阵元间距为半波长。其中,测向时的加权处理指向的是(θ+0.1θB,φ+0.1φB),约为(33°,52°)。信号的信噪比从-20 dB变化到40 dB。仿真中采用的快拍数是10 000。仿真结果是基于500次独立实验。其中
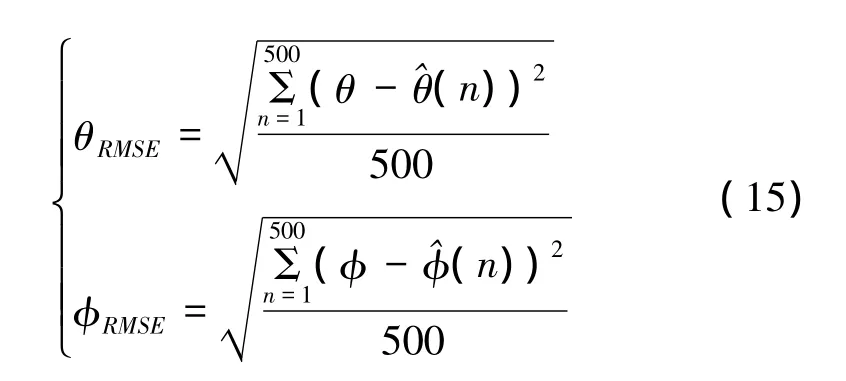

图11 测向RMSE随SNR变化曲线图
由仿真结果可以看出,测向的RMSE随着SNR增大而减小。而当信号功率大于0 dB以后,俯仰角的测向精度和方位角估计精度的测向精度变化基本保持不变。
(2)理想情况下测向精度随快拍数变化情况
假设信号依旧从(θ,φ)=(30°,50°)方向入射进来,信号的SNR设为-20 dB。仿真中采用的快拍数是从100变化到20 000,其他与(1)中的条件相同。仿真结果见图12,由仿真结果可以看出,测向的RMSE随着快拍数增大而减小。
(3)理想情况下测向精度随入射角变化情况
假设信号的SNR设为-20 dB,仿真中快拍数为50 000,俯仰角和方位角分别从-60°以2°间隔变化到60°时。仿真结果是基于200次独立实验。仿真图如图13、图14所示。
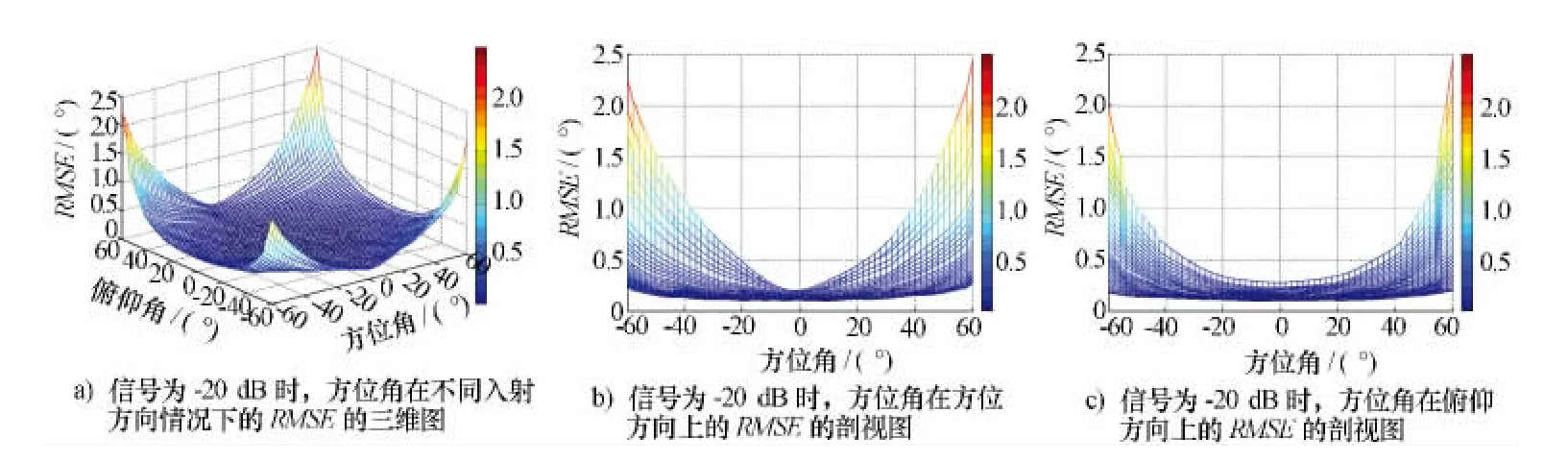
图14 方位角在不同入射方向上的RMSE
从仿真图中可以看出,俯仰角的测向精度要高于方位角上的精度。俯仰角相同,方位角不同时,俯仰角的测向精度对方位角的改变不敏感,而此时方位角精度是随方位角原理法线方向而降低。方位角相同,俯仰角不同时,俯仰角的测向精度和方位角的测向精度都随俯仰角偏离法线方向而降低。
4 结束语
本文主要针对高速运动平台条件下,相控阵卫星自跟踪系统方案设计:以双工通信为应用背景,建立卫星自跟踪系统大闭环跟踪模型,确定各模块功能和主要技术指标、工作过程、坐标变换与收发波束指向控制。结合阵天线结构与接收通道特点,设计出空域搜索方案,研究比相测角方法在本项目中的具体特点,确定测角方案,针对平台运动特性和卫星运动特点,研究和发展稳健高效的类Kalman滤波理论和实用算法是实现高速运动平台的相控阵卫星自跟踪系统的关键。本文的讨论对工程实践具有一定的指导意义。
[1]王 忠,张继宏,黄顺吉.一种改进的数字式波束形成的快速自适应算法[J].中国空间科学技术,1996(5):16-23.Wang Zhong,Zhang Jihong,Huang Shunji.An improved fast adaptive algorithm for digital beam forming[J].Chinese Space Science and Technology,1996(5):16-23.
[2]雷剑梅.基于单脉冲和自适应天线的数字单脉冲跟踪系统研究[D].重庆大学,2007.Lei Jianmei.Study on digital monopluse tracking system based on monopluse technique and adaptive antenna[D].Chongqing:Chongqing University,2007.
[3]Yang K H,Ohira T.Realization of space-time adaptive filtering by employing electronically steerable passive array radiator antennas[J].IEEE Transactions on Antennas and Propagation,2003,51(7):1476-1485.
[4]Sarcione M,Mulcahey J,Schmidt D,et al.The design,development and testing of the theater high altitude area defense solid state phased array(formerly ground based radar)[C]//IEEE International Symposium on Phased Array Systems and Technology.Boston,MA:IEEE Press,1996:260-265.
[5]牛宝君,李延波.二维相控阵单脉冲跟踪测角方法的研究与应用[J].现代雷达,2003,25(5):16-18.Niu Baojun,Li Yanbo.Study and application of angle measurement for 2-D phased array monopulse tracking[J].Modern Radar,2003,25(5):16-18.
[6]吴 越,严济鸿,何子述.基于FPGA的多通道高速数据采集系统[J].雷达科学与技术,2012,10(6):671-676.Wu Yue,Yan Jihong,He Zishu.Multichannel high-speed data acquisition system based on FPGA and USB 2.0[J].Radar Science and Technology,2012,10(6):671-676.

