基于FFT和共轭梯度法的近场诊断方法

杜 柏，李建新，2，丁 解

(1.南京电子技术研究所， 南京210039;2.天线与微波技术国家重点实验室， 南京210039)

0 引言

作为一种能够从近场的平面区域测量到的数据准确地计算出远场辐射特性的方法，平面近场测量系统被广泛采用。近场测量除了能成功计算天线的远场辐射性能参数［1］，还可以确定天线的口径场以实现对天线口径面的诊断［2-4］。在实际测量中，如果使用探头紧贴被测天线(Antenna Under Test，AUT)的方法诊断天线口径面，会由于探头与AUT之间的耦合以及多次反射，测量误差较大，造成测量结果的不准确，只能粗略地估计天线阵面的失效单元或者奇异区域的位置，而不能对其进行精确地定位。为了消除探头与AUT之间的耦合和多次反射造成的影响，一般在距离天线口径面3至10个波长的距离对AUT进行测量，再对测得的数据进行数学变换，反演得到天线口径面电场的切向分量，进而得到口径场的幅相分布。

常用的口径场反演数据处理方法有平面波谱模式展开法和等效流法。基于平面波谱模式展开的口径场变换技术发展较早，引入快速傅里叶变换(FFT)技术，运算速度快，工程实用性强。但此方法将平面波谱带宽限制在了可见域，忽略了衰减波的效应。而且，近场测量的采样间隔必须满足Nyquist定理，将采样面限定在有限尺寸也引入了截断误差，制约了诊断精度［3，5］。另一种基于等效磁流的口径场变换技术从场和源的角度出发，将天线的口径场等效为口径面上的磁流分布，通过计算该等效磁流的积分方程，反演出口径场的数据。由于此种方法可以完整考虑整个平面波的波谱，所以其诊断精度要高于模式展开法［6-8］。

探头补偿技术是近场测量中较为关键的环节。在实际测量即非理想情况中，测量所用的探头都会有自己的方向图，也就是说，测量得到的数据都是被探头方向图影响过的，并不是采样平面真实的电场。所以，为了消除探头对采样数据的影响以提高诊断精度，必须引入探头补偿技术。传统的模式展开法由于发展时间较早，而且作为理论基础的洛伦兹定理与最早出现的探头补偿理论契合度较高，探头补偿技术在该方法中发展较为成熟。而本文所采用的等效磁流法由于出现时间较晚，先前的研究中并未与探头补偿技术结合到一起，制约了诊断精度［6-9］。

本文提出的口径场诊断方法结合了以上两种方法的优点，将探头补偿技术应用于等效磁流法中。首先，采用一种新的“探头平方根法”探头补偿技术，去除测量数据中探头造成的影响;然后，将AUT前半空间辐射表示为天线口径面上等效面磁流的分布，获得一个以磁流分布为待求函数的积分方程;最后，引入矩量法，将积分方程转化为矩阵方程，应用共轭梯度法求解该矩阵方程获得天线口径面的磁流分布，进而得到天线口径面的幅相分布。为了验证本文方法的正确性及实用性，在微波暗室中对某相控阵天线进行了测量，并对比了有无探头补偿对反演结果的影响，获得了较好的结果。

1 主要理论及公式

1.1 探头补偿理论

图1为近场测量的示意图。考察一个位于z＜0的任意口径形状的天线，设其口径面与z=0平面重合，如图1所示，近场扫描面位于z=d平面。

图1 近场测量示意图

根据平面波谱展开理论以及互易原理，探头补偿的耦合方程［10］为

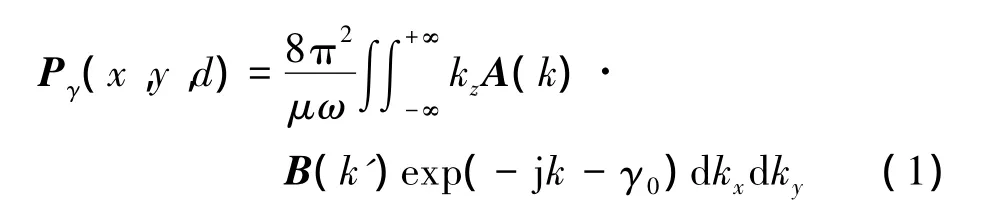
式中:Pγ(x，y，d)为探头采样到的幅相分布;A(k)为AUT在坐标系中的波谱函数;B(k')为探头在o-x'y'z'坐标系中的远场方向图矢量。也就是说对于近场测量系统，在采样面测量到的电场的波谱可以看成是AUT的发射波谱与探头的接收波谱的乘积，即P(kx，ky)=A(kx，ky)·B(kx，ky)。可以注意到，在天线的收发过程中，发射/接收可以看成一个互易的过程，即发射和接收之间可以相互转换。在理想情况下，我们期望得到的是未经探头影响过的AUT的波谱，所以，探头补偿的作用就是在计算AUT得到发射波谱时将探头所造成的影响去除掉。通常的探头补偿方法是计算实验所用的开口波导的远场方向图来建立方程计算探头的理论波谱，然后将得到的B(kx，ky)去掉，这样就可以确保P(kx，ky)中只有AUT的成分。

但是这种探头补偿方法所要求的近场校准条件是理想的，例如，必须保证探头开口平面与天线口径面是平行的。而目前的近场测试系统并不能保证如此高的精度，而且，如果探头的极化程度不是特别高，此种方法需要将探头旋转90°做两次测量，较为繁琐。所以，需要一种更为实用的方法。

假设在实验中AUT是固定不动的，本文采用了一种探头平方根法来进行探头补偿［11］。将一个与实验所采用的探头完全相同的探头放置于AUT的位置上，这意味着在此测量系统中，发射波谱与接收波谱是相同的，也就是说，可以通过测得的波谱解出探头单独的波谱，即

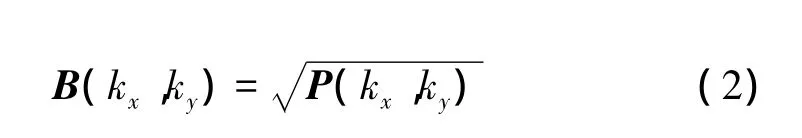
这种方法的优点是只要在实验过程中保持AUT的位置不动，就可以应用此种方法将探头对波谱的影响去除掉。这种方法还有一个优点，就是由于探头补偿与近场测量是在同一个测量系统中进行的，这种解平方根的方法还可以消除测量过程中由于测量机制所产生的误差。

这样，由式(1)可以看出，探头所测量到的采样面电场的切向分量与AUT的波谱函数和探头的接收波谱的乘积是一对二维傅里叶变换对，因此，在工程应用中，可以使用FFT来进行运算。

在去除掉探头的影响后，根据平面波谱展开理论可以得出进行探头补偿之后的采样面上的切向电场为

1.2 等效磁流模型

对于一个任意口径的天线，根据电磁场理论中的等效原理，可以将天线所在的自由空间分成两部分，如图2所示。

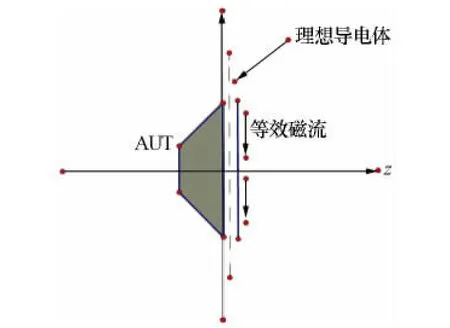
图2 等效磁场模型

假设z＜0的区域是无源的，那么在z＞0的区域内的任意位置辐射场可以完全看成是在z=0平面上的等效磁流所产生的。设将一理想导电体置于x-y平面上，即该无限大平面上切向电场为0，则该等效磁流为

式中:Es1为平面S1上的切向电场;n为平面S1的法向矢量。根据镜像原理，z＞0区域任意位置的电场可以看成是等效磁流

产生的。则在z＞0区域的任意一点的场为

取AUT的口径面为矩形区域:|x|≤Wx/2，|y|≤Wy，Wx和Wy的选取原则是确保在该矩形区域外的口径场近似为0。将口径面分为Nx×Ny个矩形小块，则各小块之间的间距为Δx=Wx/Nx，Δy=Wy/Ny，各小块的中心点坐标为

在近场测量中，由于选取的采样面一般满足d≫max(Δx，Δy)，所以引入矩量法，将口径面上的等效磁流分解成Nx×Ny个矩形小块上的二维脉冲函数的线性组合，即

式中:αij和βij为待求系数，即口径场等效面磁流的幅相分布。

对于位于z=d处的采样平面，设采样点数为Mx×My，1≤k≤Mx，1≤l≤My，则各采样点的坐标为(xk，yl，d)。为了便于计算，重新设置角标，令 N=NxNy，M=MxMy，n=i+(j-1)Nx，m=k+(l-1)M，应用点匹配法，将式(9)带入式(7)中，只考虑平面上的切向电场，得到

其中

从上面的分析中，通过一系列的数学变换，将基于等效磁流的积分方程转化成矩阵方程，下面将应用共轭梯度法求解该矩阵方程。

1.3 共轭梯度法

假设A为M×N矩阵，X和Y分别为N阶和M阶列向量，一般M＞N切矩阵均为复数。具体过程为:选定初始值X0=0，定义残差向量R0=Y-AX0，P0=AHR0，a0=‖AHR0‖2/‖AHP0‖2，c0=a0‖AHAP0‖2-‖AAHR0‖2，b0=c0/‖A P0‖2，对于 i=1，2，…，n，则有

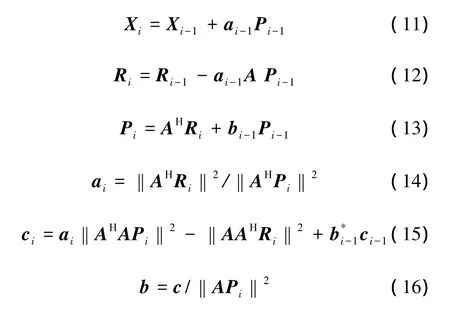
为了获得指定的精度，定义f(Xi)=‖Ri‖/‖Y‖，当f(Xi)≤e(e为要求的诊断精度)时，则认为序列Xi(i=1，2，3，…)收敛到方程的解。

2 实测诊断试验

为了验证本文口径场诊断技术的有效性和实用性以及探头补偿技术的必要性，在微波暗室中对某X波段相控阵天线进行了近场扫描诊断测试，利用测得的近场数据对天线口径场进行反演和诊断。

2.1 无探头补偿技术平面相控阵天线的口径场反演

实验采样的相控阵天线由256个天线单元按16×16的结构排列，工作频率为9.6 GHz，天线单元为缝隙波导，天线由同轴电缆通过功分网络进行馈电。实验采用的探头为X波段标准开口波导，采样面距离天线口径120 mm，沿水平方向采样点数为63，采样间隔为9.375 mm，沿垂直方向采样点数为64，采样间隔为10.937 5 mm。

为了验证算法的正确性，先只对阵列中的上数第二行波导进行供电，然后，通过对近场数据进行采样，重构出口径场的幅相分布。采样到的近场幅相分布如图3和图4所示。

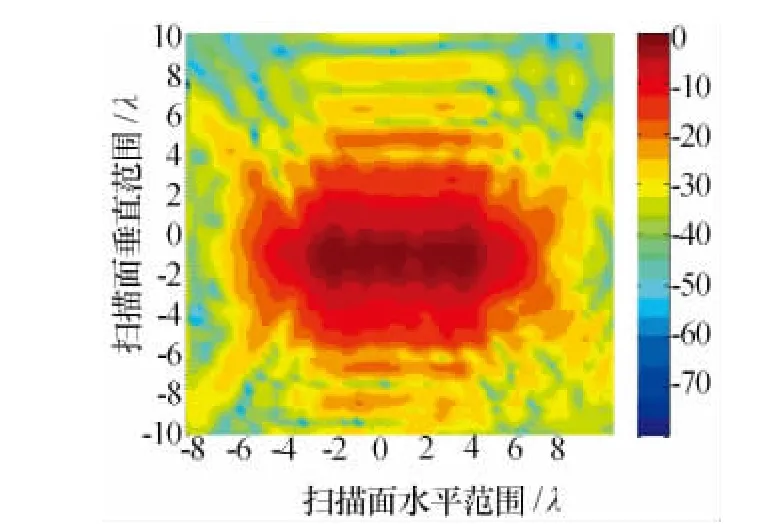
图3 单根波导供电情况下的近场幅度分析

图4 单根波导供电情况下的近场相位分布

从测得的近场数据中很难看出这是在只有一排单元供电情况下的天线近场分布，此时，运用本文的重构方法对天线口径场进行反演。由于对一排波导中的每个天线单元的供电在幅度和相位上都是均匀的，所以在理想情况下，我们会得到一个矩形的幅度和相位分布。结果如图5和图6所示。

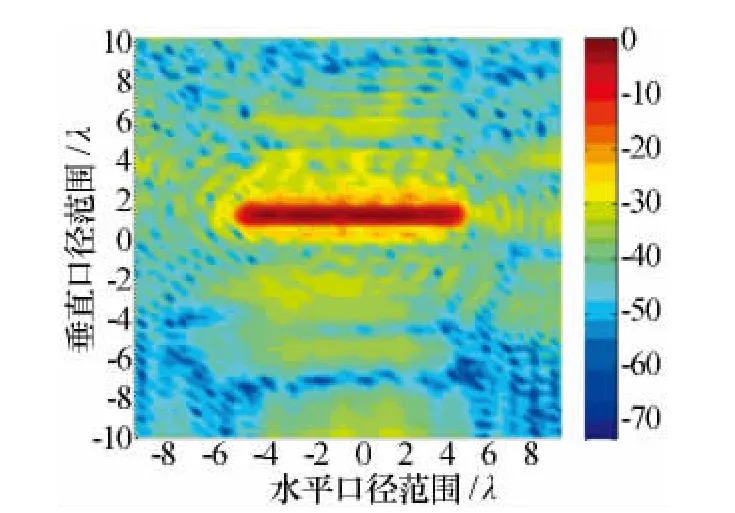
图5 单根波导供电情况下重构的口径场幅度分布

图6 单根波导供电情况下重构的口径场相位分布

从结果可以看出，反演得到的幅度比较符合预期，得到了一个矩形的辐射集中区，与试验中采用的单根波导形状相一致。而反演出的相位则与预期存在一定差异。可以清晰的看到，反演出的相位沿着图中辐射集中区的X方向有一定程度的渐变，与试验中采用的均匀幅度分布不符。此相位失真就是引入了探头的方向图造成的。可以看到，沿着此列波导，反演出的相位差达到了75°，可见引入探头补偿的必要性。

2.2 引入探头补偿技术平面相控阵天线的口径场反演

为了消除探头对采样数据的影响，提高诊断精度，本文在等效磁流法的基础上，引入了探头补偿技术。

首先，在放置AUT的位置放置一个与测量所用探头一样的探头，对其进行扫描。按照前文的方法，可以得出此探头的方向图。然后，在对AUT的测量数据进行反演前，将探头对数据造成的影响移除，得到采样面真实的电磁场。

重复上一个实验，测量对象为该相控阵天线阵面的单根波导，对采样数据进行探头补偿处理以及口径场反演，得到的结果与前文无探头补偿的口径场反演结果对比如图7所示。

图7 探头补偿前后幅度相位的对比

可以看出，采用探头补偿前后，反演得到的幅度无明显差别，但是相位的反演结果差别较大。由于波导上的辐射单元是通过同一根波导供电的，所以反演的相位理论上应该是均匀的。可以明显看到，引入探头补偿技术后，相位反演结果中的梯度被消除了，也就是说，利用此探头平方根算法可以去除测试探头本身的方向图对采样数据造成的偏差，从而有效地提高反演精度，优化诊断效果。

2.3 平面相控阵天线的口径场诊断

为进一步验证该口径场诊断方法的准确性，对该阵列天线的整个阵面进行诊断试验。首先，对全阵面进行均匀供电，以同样的采样距离和采样间隔对整个阵面进行测量，经探头补偿和口径场反演处理后，得到的结果如图8和图9所示。

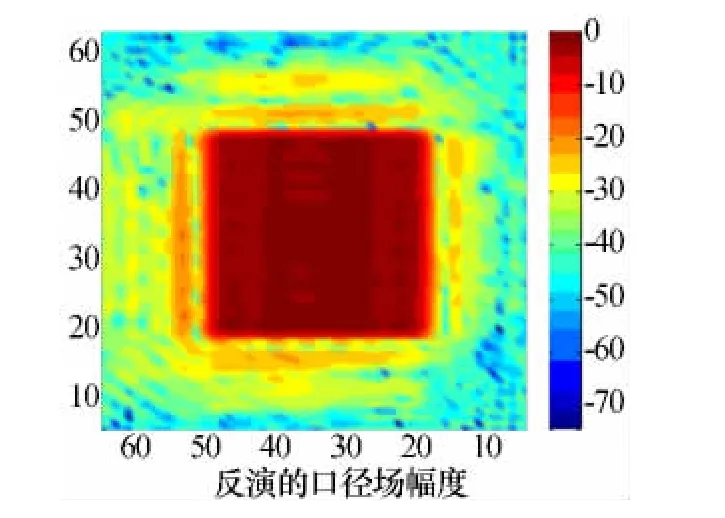
图8 全阵面供电情况下重构的口径场幅度分布

图9 全阵面供电情况下重构的口径场相位分布

可以看出，反演结果中的幅度和相位分布都是均匀的，与预期相吻合。

然后，对该天线阵面进行失效单元诊断，验证整排天线单元失效的情况。使天线阵列上数第4，5和13行波导接负载，通过使阵列上方两排天线单元以及下方一排天线单元失效来进行诊断测量，实验结果如图10所示。

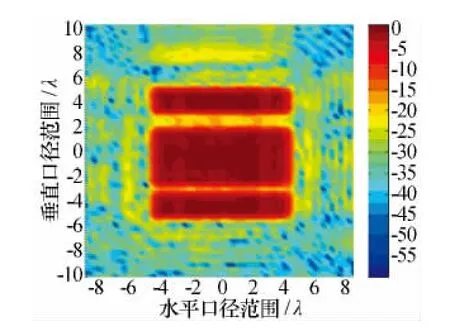
图10 整排天线单元失效诊断口径场的幅度分布

从图中可以清晰地看出，天线的口径场在上下两部分各有一块明显的不连续区域，上面的区域较宽，约为下方区域的两倍，与理论相符。结果表明:本文所提出的诊断方法可以对天线阵面的失效或不连续区域进行诊断。

3 结束语

本文提出了一种基于等效磁流与平面波谱模式展开法的相控阵天线口径场诊断方法，并对其进行了实验验证。通过对距离天线口径面四个波长的平面上的场进行采样，重构出相控阵天线的口径场对其进行诊断。既考虑了近场测量中重要的探头补偿，又通过等效磁流的积分方程计算出真实的口径场，得到了很好的结果。

［1］Kerns D M.Plane-wave scattering-matrix theory of antennas and antenna-antenna interactions［M］.Washington:United States Department of Commerce，1981.

［2］Petre P，Sarkar T K.Planar near-field to far-field transformation using an array of dipole probes［J］.IEEE Transactions on Antennas and Propagation，1994，42(4):534-537.

［3］Lee J J，Ferren E M，Woollen D P，et al.Near-field probe used as a diagnostic tool to locate defective elements in an array antenna［J］.IEEE Transactions on Antennas and Propagation，1988，36(6):884-889.

［4］Jensen F.Electromagnetic near-field far-field correlations［D］.Copenhagen:Technical University of Denmark，1970.

［5］胡鸿飞，高 雪，傅德民.基于FFT的近场-口径场变换方法［J］.微波学报，2001，17(2):1-6.Hu Hongfei，Gao Xue，Fu Demin.A transformation technique from near-field to aperture-field based on FFT［J］.Journal of Microwaves，2001，17(2):1-6.

［6］Petre P，Sarkar T K.Planar near-field to far-field transformation using an equivalent magnetic current approach［J］.IEEE Transactions on Antennas and Propagation，1992，40(11):1348-1356.

［7］Taaghol A，Sarkar T K.Near-field to near/far-field transformation for arbitrary near-field geometry，utilizing an equivalent magnetic current［J］.IEEE Transactions on Electromagnetic Compatibility，1996，38(3):536-542.

［8］胡鸿飞，傅德民，李 勇.基于等效磁流的近场诊断方法［J］.西安电子科技大学学报(自然科学版)，2001，28(1):52-56.Hu Hongfei，Fu Demin，Li Yong.A near-field diagnostic method based on equivalent magnetic currents［J］.Journal of Xidian University，2001，28(1):52-56.

［9］陈 瑞，胡明春，李建新.平面近场测量中一种口径场重构技术研究［J］.现代雷达.2010，32(6):67-72.Chen Rui，Hu Mingchun，Li Jianxin.A study on aperture field reconstruction technology in planar near-field measurements［J］.Modern Radar.2010，32(6):67-72.

［10］Leach W M，Paris D T.Probe-compensated near-field measurements on a cylinder［J］.IEEE Transactions on Antennas Propagation，1973，21(4):435-445.

［11］Masters G F.Probe-correction coefficients derived from near-field measurements［C］//AMTA Conference.Carson，CA:AMTA Press，1991.