不同渠道经费对科学与技术贡献的比较研究——基于空间面板模型的估计

俞立平

（宁波大学 商学院，浙江 宁波315211）

一、引 言

从宏观视角研究科研经费投入的绩效是一个经典的命题。从经费来源渠道看，目前的投入渠道主要有三个：第一是企业投入，这是研发投入的主体；第二是政府投入，体现了国家对科技创新重视的力度，是研发投入的必要补充；第三是银行科技贷款，用来暂时弥补前两项投资的不足。当然对于同一研发主体而言，其研发投入可以同时包括以上三个方面的来源，特别是从国家与地区的视角。从科技创新产出来看，也可以分为两大类，一是基础科学创新，二是应用技术创新。总体上，企业以技术创新为主，高校、科研院所等兼顾基础科学与应用技术创新。究竟哪些投入用于基础科学，哪些投入用于应用技术，目前并没有详细的统计数据，相应地也缺乏对不同渠道研发经费投入对基础科学与应用技术贡献的比较研究（图1）。

地理学第一定律认为，几乎所有空间数据都具有空间依赖或空间自相关特征。在科技投入产出中，知识和技术的积聚与扩散是非常普遍的现象，比如北京、上海等中心城市都有着较强的科技与人才积聚，而这些积聚对周边地区不断产生科技扩散。随着互联网的发展，知识与技术的积聚扩散又呈现出新的特点，信息传播的快捷加大了知识与技术的空间效应，在这样的背景下，研究不同渠道研发经费投入对科技创新的贡献必须充分考虑不同地区之间空间上的互相影响。

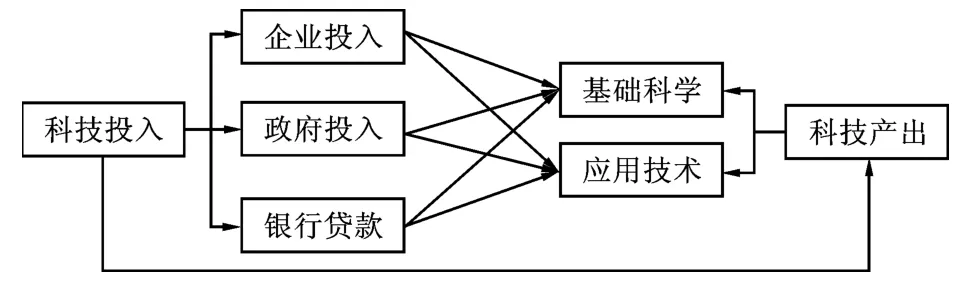
图1 研发投入渠道与科技产出关系图

对不同渠道研发经费的绩效进行比较其意义是毋庸置疑的，如果在此基础上进一步研究这些不同来源渠道研发经费对基础科学与应用技术的贡献，则更具备全局的视野。可以比较政府经费、企业经费、银行科技贷款的贡献大小以及同样投入经费对基础科学与应用技术贡献的特点，分析其中存在的规律与问题，便于政府从宏观角度加强科研经费管理，合理分配有限的科技资源，改进科技金融政策，因而具有十分重要的理论意义与实践价值。

国外对政府科技投入的关注始于Nelson、Porter等学者的研究，其主要方法是对各国政府科技投入的不同方式、政府支持科技创新的不同政策等进行比较，继而开始政府研发投入、企业研发投入的绩效研 究［1］［2］97－103。Carpon 估 计 了 各 种 不 同 资 金 来源研发经费的效率，同时还估计了这些经费对于自身R＆D投资的刺激效应［3］。Dominique等实证研究了政府科技投入对企业R＆D投入的影响作用［4］。Bettina等发现政府投入对低技术产业R＆D投入带动作用显著，而对高技术产业R＆D投入引领作用不显著［5］。Lach通过对以色列制造业的研究发现，政府R＆D投入能带动小企业R＆D投入［6］。Guellec等通过对17个OECD国家的研究发现，中等政府经费资助强度对企业研发投入的激励效果较好［7］。Blank等通过对1 564家制造业企业的研究发现，获得政府资助的企业有比较低的研发人力资源比例，即研发政府资助对企业人力资源存在某种替代效应［8］。Klette等采用面板数据对挪威816个电子电气行业的实证研究发现，政府投入经费对企业经费有带动效应，对小企业与大企业的带动效应超过中等企业［9］。对银行科技贷款绩效的研究相对较少，肖科采用结构方程模型测度政策性金融对中国自主创新成果转化的贡献［10］。王海等根据科技资金投入与科技活动产出过程的特点，提出了评价科技金融结合效益的指标体系和效益评价模型［11］。

在知识与技术的空间与溢出效应研究领域，最早也是国外学者进行研究。Cohen等认为创造知识是R＆D活动的主要目的，这些新的知识会在不同地理空间的地区发生溢出效应［12］。Keller等研究了技术溢出效应与地理空间距离的关系，发现技术溢出效应与地理空间距离负相关［13］。Lakshmi采用1975—1986年印度私营制造企业的面板数据研究发现，研发投入溢出效应比较明显，会带来额外增加的产出［14］。Anselin等利用美国大学研发和高新技术创新数据，采用空间计量经济方法，发现R＆D溢出效应超越了地理边界［15］。Greunz认为选择区位时要与技术层次相近的区域以及技术领先的区域相邻［16］。

从以上研究看，关于科技投入产出的研究成果较为丰富，既有宏观层面的研究，也有微观层面的研究，研发主体既有国家区域，也有广大企业、高校和科研院所。考虑知识与技术空间溢出效应的实证研究也比较丰富，总体上尚存在以下问题：

第一，“科技”一词在不同语境下的内涵是不一样的，有时指科学与技术，有时是偏义复词，特指技术。将基础科学与应用技术分离，比较不同投入要素贡献的研究不多。

第二，从投入要素的角度，现有的研究往往集中在政府经费与企业经费的绩效比较以及政府研发投入对企业研发投入的关系，缺乏从政府投入、企业投入、银行科技贷款三个角度进行研究。

第三，从研究方法看，采用空间计量模型的研究总体不多。此外，随着现代信息技术的发展，知识与技术溢出已经在传统空间影响的基础上呈现出新的特点，如果继续采用传统的地理位置相邻作为权重矩阵设置依据是值得商榷的。

本文基于中国省际面板数据，首先对基础科学与应用技术的空间相关特征进行比较，然后在考虑空间依赖与相关的基础上，采用空间面板数据模型，比较企业研发经费、政府研发经费、银行科技贷款对基础科学与应用技术贡献的弹性系数，总结分析不同投入途径、不同产出视角下投入要素的绩效特点，分析其中深层次的作用机制与存在的问题，在此基础上进行深入讨论。

二、研究方法

（一）Moran’s I指数

全局空间相关指数 Moran’sI最早由 Moran于1950年提出［17］，其表达式为：

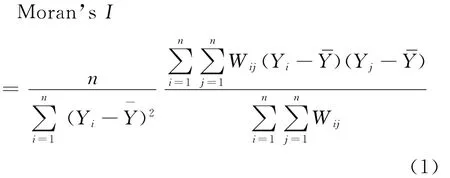
式（1）中，Yi、Yj分别表示i，j两个地区某个考察指标的观测值，n为相对独立的地理空间单元个数，Wij为空间权重矩阵，用来测度i，j两个地区间的空间依赖关系，一般采用二进制空间权值矩阵，通常情况下相邻地区值为1，不相邻地区为0。全局空间相关指数 Moran’sI取值范围为－1≤I≤1，－1表示完全空间负相关，1表示完全空间正相关，等于0表示空间不相关。类似地，局部空间相关指数用于分析某个考察指标局部地区与相邻地区的相关程度，本文主要分析全局指数。

关于权重矩阵设置，在现代信息社会下，由于知识与技术的传播很快，采取传统的地理位置相邻与否的设置方法是值得商榷的，考虑到基础科学与应用技术主要以自然科学领域为主，因此本文采用地区间作者合作论文数量作为权重矩阵的设置依据，数据来自于中国科学院文献情报中心的CSCD数据库，具体处理方法是，在研究时间段内，检索两个地区合作的论文数量，作为这两个地区空间依赖与相关大小的依据，两地作者合作论文越多，说明两地的基础科学与应用技术的依赖程度越强。

（二）面板空间计量模型

面板数据空间计量模型目前主要有两种，第一种是空间滞后模型（Spatial Lag Model，SLM），人们也称其为空间自回归模型（Spatial Autoregressive Model，SAR），之所以有这种说法，是因为在回归模型中引入了空间滞后因变量，用于测度空间互动关系的存在与否及其强度；第二种是空间误差模型（Spatial Error Model，SEM），在回归模型中加入残差结构的特殊形式，用于处理空间自回归变差的影响。究竟采用哪种模型的检验方法主要有Moran、LMerr、LMsar、Lratios、Walds等检验，它们的原假设为H0：ρ＝0或λ＝0，如果拒绝，分别表示应该采用空间滞后模型或空间误差模型。

1．空间滞后模型

空间滞后模型SLM的数学表达式为：

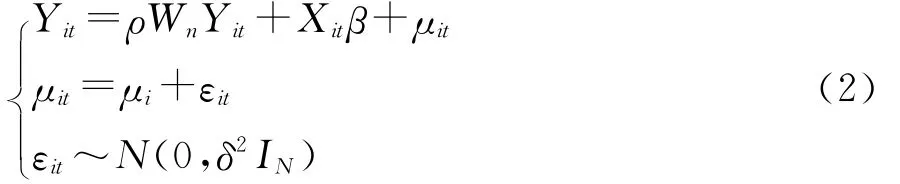
式（2）中，Yit为被解释变量矩阵，Xit为解释变量矩阵，Wn为空间权重矩阵，WnYit的乘积表示被解释变量的空间自回归矩阵，说明一个空间单元上的被解释变量既与该地区的解释变量相关，也与相邻地区的被解释变量相关。ρ为被解释变量空间滞后矩阵的系数，如果其显著地不为0，说明被解释变量相邻地区空间单元之间存在扩散、溢出等相互作用，即存在空间依赖。β为因变量Xit的回归系数矩阵，μit是与空间单元相关的空间效应，包括固定效应和随机效应两种，εit是服从正态分布的随机误差项。

Griliches和Jaffe将Cobb－Douglas生产函数改进后应用到科技研发中，提出Griliches－Jaffe知识生产函数，投入要素为研发经费（K）和研发人员（L）［18－19］。本文将研发经费进一步分解为企业研发经费（K1）、政府研发经费（K2）、银行科技贷款（K3），当然银行科技贷款本质上仍然属于企业研发投入，进一步细分是为了研究科技金融的绩效。此外从减少异方差的角度出发，对所有变量均取对数处理，这样回归系数表示产出弹性，解释度更好。式（2）进一步改进为：

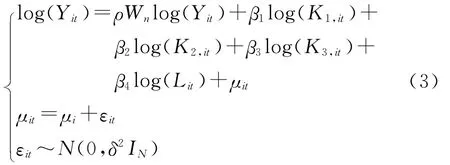
2．空间误差模型

空间误差模型SEM的表达式为：

式（4）中，λ为截面被解释变量矩阵的空间误差系数，反映相邻地区被解释变量残差的冲击对本地区因变量观察值的影响程度，也就是说，空间误差模型的空间依赖作用存在于随机误差项μit中，说明一个地区对周围地区的影响更多地体现在整体的结构性特征冲击中，并非单纯是被解释变量之间的相互作用冲击和影响。同样将研发经费细分为企业研发经费（K1）、政府研发经费（K2）、银行科技贷款（K3），将式（3）进一步整理得：

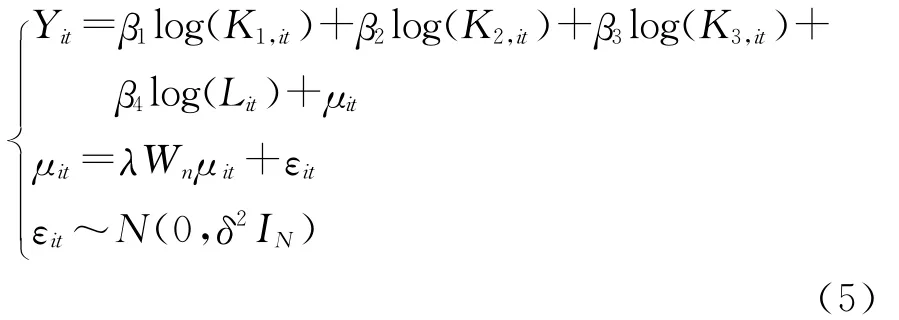
对于空间面板模型估计，若用传统的最小二乘法OLS回归会导致参数有偏，一般采用极大似然法进行估计，除此以外还有工具变量法和广义矩方法（GMM），考虑到后者需要提供工具变量，对面板数据而言找到合适的工具变量更加困难，本文采用相对成熟的极大似然法进行估计。

三、数 据

首先必须找到基础科学与应用技术两个因变量的合适表示。科学是全人类的，其研究成果具有公共产品特性，因此本文选取国际三大检索论文数作为基础科学的产出指标，但是SCI、EI、ISTP三大检索论文是3个指标，必须进行归一化处理，考虑到会议论文时效性虽然好，但更具有探索性，在征求中国科学技术信息研究所、中国科学院文献情报中心相关专家的基础上，三大检索论文的权重依次为0．7、0．2、0．1，所有数据归一化后进行汇总。本文选取授权的发明专利、实用新型专利、外观设计专利作为技术创新变量，采取与三大检索论文权重同样的方法确定其权重为0．7、0．2、0．1，当然也在标准化后进行汇总。研发投入经费变量有企业研发经费、政府研发经费和银行科技贷款，研发人员变量选取研发人员全时当量，采用该指标比单纯选取研发人员数量要相对合理。

所有数据均来自于2002—2009年期间的《中国科技统计年鉴》。需要说明的是，之所以选取这一区间主要有两个原因，第一是2000年以后互联网在中国开始大规模普及，互联网时代与非互联网时代的空间权重矩阵设置方法是不一样的。第二是缺乏2000年分省的国际三大检索论文统计数据，同时也缺乏2009年以后的分省的企业研发经费、政府研发经费、银行科技贷款数据。此外，西藏自治区由于部分年度数据缺失没有选取，所有数据的摘要描述统计量如表1所示。

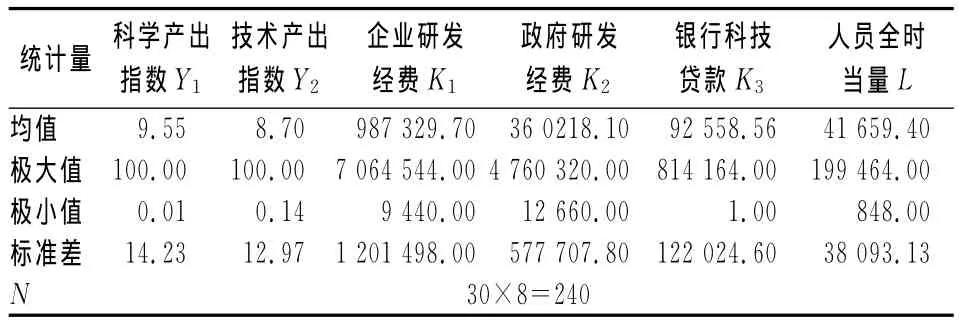
表1 摘要描述统计量表

四、实证结果

（一）历年各地区的 Moran＇s I指数

2001—2008年期间历年中国省际基础科学与应用技术的Moran＇sI指数如表2和图2所示，基础科学的空间相关指数均值为0．510，应用技术的空间相关指数均值为0．492，两者水平比较接近，无论基础科学还是应用技术总体上均存在明显的空间相关。从曲线的动态变化看，基础科学的空间相关指数波动要比应用技术大，并且基础科学的空间相关指数处于动态波动状态，这是由知识的特点所决定的，以论文体现出来的知识是共享的，地区间通过知识的溢出效应产生影响，一旦偏离均值，知识的溢出效应会减少地区间的知识差距，其周期一般是1到2年，符合互联网背景下知识生产、传播、共享、借鉴规律。

应用技术相对而言比较稳定，其空间积聚与扩散效应与基础科学是完全不一样的，其内在机制有很大的区别。以专利为代表的应用技术具有独享性，其空间依赖更多体现在技术带来的示范效应，而非技术传播本身，因为专利是不可能无偿传播的。在这种情况下，技术的空间相关指数体现出稳定的趋势，曲线波动较小。

表2 历年科学与技术的Moran＇s I指数表

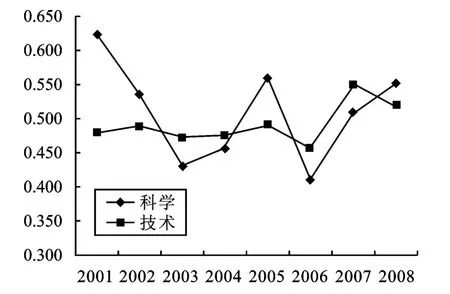
图2 历年中国科学与技术的Moran＇s I指数

（二）面板数据的平稳性检验与协整

面板数据在回归分析前要进行平稳性检验，以防止出现伪回归问题，面板数据单位根检验方法有ADF fisher检验、Levin Lin＆Chu检验、PP fisher检验等，不同检验方法原理不同，检验结果也不尽相同，从提高稳健性的角度，以3种方法结果一致为准，结果如表3所示，所有变量经过1阶差分后都是平稳时间序列。

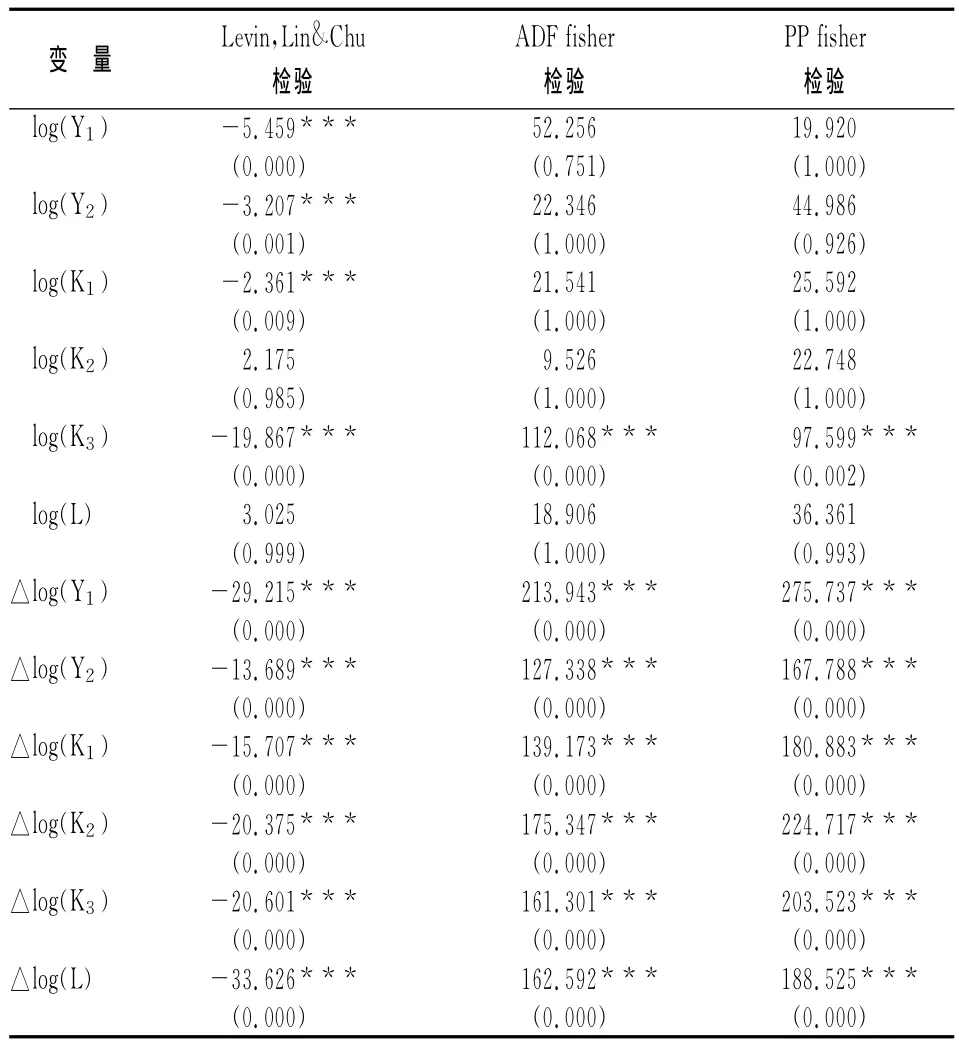
表3 面板数据的平稳性检验表

下面进行面板数据的协整检验，以验证基础科学与应用技术产出与研发经费投入及研发人员投入之间是否存在长期稳定的协整关系，采用KAO面板协整检验，结果t检验值为－8．488，相伴概率为0．000，说明基础科学、应用技术、企业研发经费、政府研发经费、银行科技贷款、研发人员全时当量之间存在长期稳定的均衡关系，可以进行进一步的回归分析。

（三）基础科学投入产出估计

对于空间面板数据的估计，究竟是采用传统的最小二乘法还是极大似然法进行估计，必须首先进行空间相关性检验，常用的检验方法有LMerr、Robust＿LMerr、LMsar、Robust＿LMsar等，最早这些检验方法都是面向截面数据的，后来Elhorst将其推广到面板数据［20］。空间自相关检验结果如表4所示，LMsar、Robust＿LMsar、Robust＿LMerr均在1%的水平下通过了统计检验，LMerr在5%的水平下通过了统计检验，最终确定选择LMsar模型，采用极大似然法进行估计。

表4 基础科学投入产出的空间自相关检验表

根据Baltagi的研究，如果样本是随机地从总体中抽取时，应该选择随机效应模型，否则应该采用固定效应模型［21］45－53。本文选取的是除西藏外大陆30个省市的样本数据，接近总体，因此选择固定效应SLM模型进行估计，为了便于比较，还给出了传统面板数据随机效应模型以及空间误差模型的估计结果。

模型估计结果见表5，从空间滞后模型SLM固定效应的估计结果看，企业研发经费在5%的水平上通过了统计检验，政府研发经费在1%的水平上通过了统计检验，银行科技贷款与研发人员全时当量没有通过统计检验，模型具有较高的拟合优度，R2为0．988，空间滞后向量ρ在1%的水平上通过了统计检验，说明空间效应明显。对基础科学产出而言，政府研发经费的弹性系数最大，每增加1%会带来基础科学产出增加0．348%，企业研发经费次之，每增加1%会带来基础科学产出增加0．149%。

从传统面板数据与空间误差模型的结果看，也是银行科技贷款与研发人员全时当量没有通过统计检验，并且政府研发经费对科学产出的贡献大于企业研发经费，与空间滞后模型的估计结果基本类似，说明结果是稳健的。

从回归系数的大小看，传统回归高估企业研发投入和政府研发投入对基础科学的贡献，原因是没有考虑到知识的空间相关性引起的。

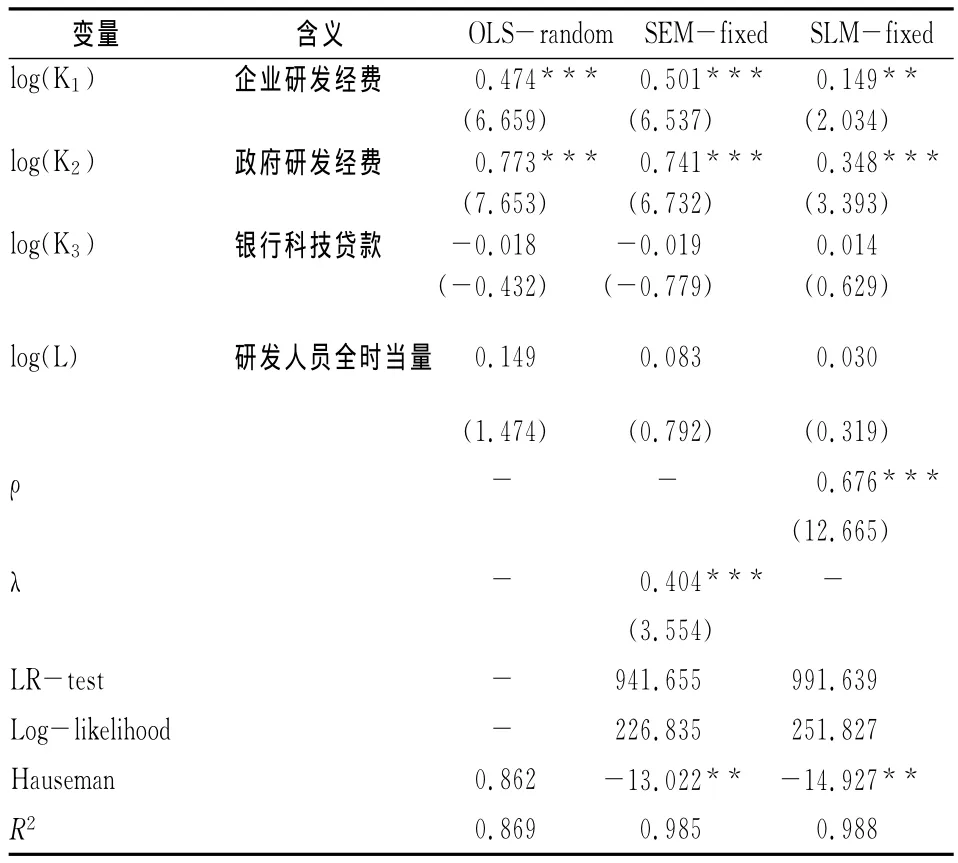
表5 基础科学投入产出的面板数据估计表

（四）应用技术投入产出估计

应用技术投入产出的空间相关检验结果如表6所示，LMsar、Robust＿LMsar、LMerr在1%的水平上通过了统计检验，Robust＿LMerr没有通过统计检验，很明显要选择SLM模型进行估计，为便于比较，同样给出了空间误差模型与传统固定效应模型的估计，表7为估计结果。

表6 应用技术创新产出的空间自相关检验表

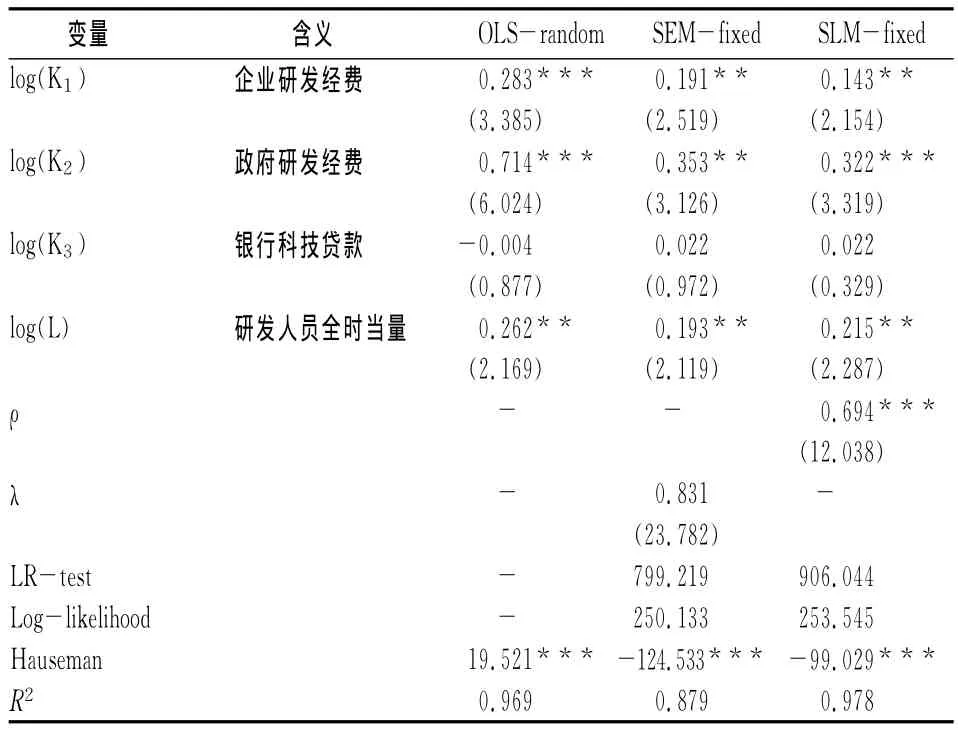
表7 应用技术创新产出的面板数据估计表

从空间滞后模型SLM固定效应的估计结果看，企业研发经费和研发人员全时当量在5%的水平上通过了统计检验，政府研发经费都在1%的水平上通过了统计检验，银行科技贷款没有通过统计检验，模型具有较高的拟合优度，R2为0．978，空间滞后向量ρ在1%的水平上通过了统计检验，说明空间效应明显。对应用技术创新而言，政府研发经费的弹性系数最大，每增加1%会带来应用技术增加0．322%；研发人员全时当量次之，每增加1%会带来应用技术创新增加0．215%；企业研发经费最低，每增加1%会带来应用技术创新产出增加0．143%。从回归系数的大小看，传统回归高估了企业研发投入和政府研发投入对应用技术创新的贡献，原因是没有考虑技术创新的空间相关性。

从传统面板数据与空间误差模型的结果看，也是银行科技贷款没有通过统计检验，研发人员全时当量通过了统计检验，并且政府研发投入对应用技术的贡献大于企业投入，总体上模型是稳健的。

五、结 论

（一）基础科学与应用技术的空间溢出效应并不相同

以三大检索论文为代表的基础科学，由于论文是公开发表的，加上现代信息技术的发展，知识传播与扩散相对比较容易，一旦空间相关指数出现波动，知识的空间溢出效应能够对此产生反应，但会有1～2年的滞后期，这也符合科技论文的写作和传播规律。而以专利为代表的应用技术，本质上是互相保密的，其技术溢出更多体现为一种“示范”影响，因此空间相关指数波动较小。

（二）政府研发经费的绩效总体良好

无论是将基础科学作为产出还是应用技术作为产出，政府研发经费的贡献的弹性系数都大于企业研发经费的弹性系数，但是其中的作用机制并不相同。对以国际三大检索论文为代表的基础科学而言，它具有明显的公共物品特征，政府研发投入理应作为投入主体，发挥主导作用。

对以专利为代表的企业技术创新而言，企业所有研发投入中政府研发投入已经不占主导地位，企业自有资金是研发投入的主体，在这样的背景下政府研发经费的弹性系数仍然大于企业研发经费，说明政府研发投入的“目标性”较好，绝大多数投入到了创新较强的企业中去，绩效良好。政府研发经费对企业研发经费具有带动作用，也增强了这种效果。

（三）研发人员全时当量对应用技术的贡献更加明显

实证研究表明，研发人员全时当量对基础科学没有贡献，而对应用技术创新的贡献比较显著，其弹性系数超过了企业研发经费的弹性系数。研发人员投入对基础科学与技术创新的作用机制并不相同，对基础科学而言，有的领域投入较大，有的领域投入较小；有的领域团队人数众多，有的领域团队人数较少；有的学科论文产出相对容易，而有的学科论文产出比较困难，从而导致了研发人员全时当量对基础科学贡献不够显著。而对以专利体现的应用技术创新而言，形态相对比较单一，不同产业之间的差别相对较小，因而研发人员全时当量的贡献比较鲜明。

（四）银行科技贷款的绩效较低

无论对基础科学还是应用技术，银行科技贷款都没有通过统计检验，说明银行科技贷款的绩效较低。在国家科技创新系统中，银行科技贷款主要是以企业为主体筹措的，创新也以应用技术为主，然而技术创新的风险性与商业银行的风险规避性天生是一对矛盾，商业银行更愿意贷款给那些有担保、风险较小、收益稳定的单位与项目。在这样的情况下，一方面企业对银行科技贷款有较大的需求，而银行却不愿意提供必要的资金支持，从而导致银行科技贷款占整个科技投入的比例较小，并且绩效不高。要彻底解决这个问题，政府必须发挥主导作用，充分考虑到技术的溢出作用，加大对科技金融的支持力度，出台一系列政策措施，以加快技术创新的步伐。

（五）知识与技术溢出对研发要素投入弹性具有“挤出效应”

无论是基础科学还是应用技术的投入产出，传统面板数据模型均高估了投入要素对科学与技术的贡献。也就是说，将要素投入对基础科学与应用技术的贡献全部归功于要素投入本身，而忽视了知识与技术溢出效应对创新产出的贡献。空间面板估计认为投入要素对科技产出的贡献既包括投入要素自身的贡献，也包括知识与技术溢出效应的贡献，正因为知识与技术的溢出对要素投入弹性具有挤出效应，从而导致了传统面板数据模型高估了要素贡献的弹性。

［1］ Nelson R R．The Simple Economics of Basic Scientific Reaearch［J］．Journal of Finance，1959，49（3）．

［2］ 迈克尔·波特．国家竞争优势［M］．李明轩，邱如美，译．北京：中信出版社，2007．

［3］ Carpon H，Van Pottelberghe B．Public Support to R＆D Programmes：An Integrated Assessment Scheme［R］．OECD，1997．

［4］ Dominique Guellec，Bruno Van Pottlesberghe．The Impact of Public R＆D Expenditure on Business R＆D［R］．Paris OECD Working Paper，2000．

［5］ Bettina Becker，Hall Stephen G．The Determinants of High－Tech Versus Low－Tech R＆D Investment：Evidence from Testing the Pooling Assumption［C］．NIESR Discussion Papers，2003．

［6］ Lach S．Do R＆D Subsidies Stimulate or Displace Private R＆D？Evidence from Israel［R］．NBER Working Paper No 7943，2000．

［7］ Guellec D，Van Pottelsberghe B．Does Government Support Stimulate Private R＆D？［R］．OECD Economic Studies，1999．

［8］ Blank David M，Stigler George J．The Demand and Supply of Scientific Personnel［R］．New York，National Bureau of Economic Research，Inc．，1957．

［9］ Klette，Tor Jakob，Jarle Moen．R＆D Investment Responses to R＆D Subsidies：A Theoretical Analysis and Microeconomic Study［R］．Mimeo，Oslo，1998．

［10］肖科．政策性金融对我国自主创新成果转化的贡献研究［J］．科技进步与对策，2009（12）．

［11］王海，叶元煦．科技金融结合效益的评价研究［J］．管理科学，2003（4）．

［12］Cohen W，Klepper S．The Trade off between Firm Size and Diversity in the Pursuit of Technological Progress［J］．Small Business Economics，1992（4）．

［13］Keller W．Geographic Localization of International Technology Diffusion［J］．American Economic Review，2002，92（1）．

［14］Lakshmi K Raut．R＆D Spillover and Productivity Growth：Evidence from Indian Private Firms［J］．Journal of Development Economics，1995，48（1）．

［15］Anselin L，Attila Varga，Acs Zoltan J．Local Geographic Spillovers between University Research and High Technology Innovations［J］．Journal of Urban Economics，1997，42（3）．

［16］Greunz L．Geographically and Technologically Mediated Knowledge Spillovers between European Regions ［J］．Ann．Reg．Sci．，2003，37（4）．

［17］Moran P A．Notes on Continuous Stochastic Phenomena［J］．Biometrika，1950，37（17）．

［18］Griliches Z．Issues in Assessing the Contribution of Research and Development to Productivity Growth［J］．Bell Journal of Economics，1979（1）．

［19］Jaffe A B．Real Effects of Academic Research［J］．The American Economic Review，1989（5）．

［20］Elhorst P．Specification and Estimation of Spatial Panel Data Models［J］．International Regional Science Review，2003（26）．

［21］Baltagi B H．Econometrics Analysis of Panel Data［M］．Chichester：John Wiley，2001．