经济预警指数、国房景气指数与CPI指数波动溢出实证分析——基于三元 VAR－GARCH－BEKK模型

张宇青，周应恒，易中懿

（1南京农业大学 经济管理学院，江苏 南京210095；2江苏大学 党委，江苏 镇江212013）

一、引 言

改革开放以来，随着中国住房制度和城市土地使用制度的不断完善，房地产业取得了迅猛发展，成为拉动中国经济快速增长的主导力量之一，住房与城乡建设部的统计数据表明：多年来房地产业对经济增长的贡献率一直保持在2%以上，并且产生了大量的就业岗位。房地产业的火爆加速了通货膨胀，房价高涨促使国际、国内热钱大量投资于地产业，各种资源要素（劳动力、建筑原材料、土地）的成本大幅攀升，造成了货币购买力的急剧下降和居民储蓄预防性动机的提高。房价上行会引起有效购买力不足，开发商囤积了大量土地、资金回笼难度高，当地产业萎缩时会造成与之相关的钢铁、物流、建筑产业增速下滑，整个工业体系将会面临巨大挑战。从财政层面看地方政府巨大的债务偿还工作也因地产业疲软而陷入困境，国际货币基金组织（IMF）认为中国金融系统对地产业的“间接头寸”巨大，国有五大银行的50%以上抵押品是土地和物业，地产缩水必然导致金融资产缩水和流动性风险。因为经济系统中信息、资源流动的加快，宏观经济与物价水平波动同样也会对地产业造成显著影响，因为良好的经济环境促使企业加大固定资产投资从而推动地产业发展，在CPI上扬时居民也出于资产保值目的加剧购房行为，造成房价变动。

总而言之，宏观经济、国房景气、物价水平三者之间存在着很强的关联性。同时，三个指数之间还可能存在着 “波动溢出”效应：某一指标当期波动程度不仅取决于自身前期波动和前期残差平方，也取决于其他指标前期波动和前期残差平方，即不同指标之间存在传染效应，本质上是一种风险传递的内在行为。本文拟采用三元VARGARCH－BEKK模型进行分析，主要目的是：检验经济预警指数、国房景气指数、CPI指数三者间是否存在波动溢出效应，以及波动溢出效应在三者之间的单双向特征。

二、文献回顾

目前理论界对于宏观经济、房地产业、物价之间的关系研究非常多，根据两两关系可以归结为以下三种：

（一）宏观经济与物价的关系

姚小剑认为宏观经济增长超越潜在GDP，造成了总供给与总需求关系的不平衡，从而引发价格波动［1］；孔繁龙和道加华旦使用相关系数与Granger因果分析法证实了物价与经济增长之间存在着显著因果关系，并且经济增长对物价产生影响的时滞期为1年［2］。

（二）宏观经济与房价关系

张勇等人使用典型相关分析和逐步回归方法得出了宏观经济对地产业的影响非常显著，主要是因为地产业的产业关联度很强［3］；位志宇等人利用上海房地产市场数据分析认为地产市场存在 “羊群行为”时，宏观经济基本面与地产价格关系会发生扭曲，进一步使房价上涨并引发经济泡沫［4］；强林飞等人认为银行信贷、地产价格和宏观经济间存在长期协整关系，当波动偏离发生时，系统会进行恢复调整［5］。但也有学者认为房地产价格波动不影响物价稳定和经济增长的前提下，按照泰勒规则政府干预地产价格时会有损失［6］。

（三）物价与房地产业关系

黄飞雪和金建东认为房地产价格指数与CPI关系适宜用非线性STR模型进行实证，结论显示地产价格增加对CPI有正向推动作用［7］；汪小亚和代鹏认为中国现阶段资产价格变化对控制通胀是次要参考依据，地产价格上升是CPI推动的，但反向关系却不存在［8］；范万志等人借用Mishkin理论认为房价通过财富效应、托宾Q效应、企业与家庭的资产负债表等4个路径催生通胀压力［9］。

上述对宏观经济、物价、房地产业间的关系研究大部分集中于绝对值视角，即考虑一个指标变动对其他指标的影响，只考察了三者间的直接影响效应，对指标相互之间的波动溢出效应缺乏分析。本文认为在考虑经济系统中指标的绝对冲击效果的同时，还需要考虑相互间的波动影响关系，因为这是控制风险的必要前提，多元GARCH－BEKK模型能够较好的解决这个问题，下文采取该方法对中国经济预警指数、国房景气指数和CPI指数间的波动溢出效应进行检验，为中国有关经济政策的制定提供理论依据。

三、模型设定与变量描述

（一）VAR－GARCH－BEKK模型

Engle和Kroner（1995）在单变量GARCH 模型基础上提出了一种测算多变量间波动溢出的BEKK算法，该算法利用向量自回归（VAR）模型得出的方差—协方差信息进一步构造非对称的多元GARCH模型。设一个包含了三个内生变量的向量可表示 成Yt＝ （Y1t，Y2t，Y3t）＇，将 三 元 GARCHBEKK模型表示为：

式（1）是以VAR（p）形式表现的内生变量滞后影响均值方程，Yt是3维列向量，a0是3维常数列向量，ai是滞后第i阶的3×3阶自回归系数矩阵，εt是3维残差列向量；式（2）是针对残差矩阵建立的BEKK形式的方差方程，Ht是3×3阶在t时刻条件残差的方差－协方差矩阵，C是3×3阶下三角矩阵，A、B均为3×3阶待估计系数矩阵，其中A表示ARCH项，B表示GARCH项。A、B中对角线元素aii，bii体现了自身残差平方滞后期和滞后波动给本期波动带来的影响，如果统计上不显著，说明不存在ARCH和GARCH效应，这点与单变量GARCH模型类似；aij，bij（i≠j）体现了某一变量过去异常冲击对另一变量的条件波动发生改变和波动外溢情况，即ARCH型和GARCH型波动溢出影响。针对波动溢出检验，目前主要有 Wald检验和似然比检验方法，但一些学者认为在估计参数时因为变量系数呈现为非线性形式，而传统的 Wald检验在非线性约束下不稳定，所以波动溢出检验只要对估计参数的显著性与否进行检验即可［10］。本文不将有关检验的步骤一一列出，有兴趣的读者可参照有关教程和文献。

（二）变量描述

本文选择经济预警指数（MPWI）、国房景气指数（SHBI）、居民消费物价指数（CPI）分别作为宏观经济运行、房地产业发展、物价情况的指标，MPWI是把经济运行状态分为5个级别：“红灯”表示经济过热，“黄灯”表示经济偏热，“绿灯”表示经济运行正常，“浅蓝灯”表示经济偏冷，“蓝灯”表示经济过冷，用于衡量一定时期内的宏观经济景气状况；SHBI从土地、资金、开发量、市场需求等角度显示全国房地产业基本运行状况（包括波动幅度、未来趋势等），从而为国家宏观调控提供预警参考；CPI是根据与居民生活有关的产品及劳务价格统计出来的物价变动指标，通常用于观察通货膨胀水平。本文采取样本期为2005年2月至2013年5月的月度数据，数据来源于“同花顺”数据中心，因为国房景气指数各年1月份数值缺失，故采取相近月份数值进行平均法填补。

采用EVIEWS6．0软件进行基本统计描述（见表1），发现MPWI和SHBI均为左偏态，CPI为右偏态，MPWI序列标准差为11．602，在三个序列中最大，说明波动最剧烈。J－B统计量显示MPWI和CPI序列服从正态分布，而SHBI则拒绝正态分布假设，三个序列的峰度系数小于3，不存在尖峰特征。从序列相关的滞后6和12阶Q统计量来看，三个序列均存在自相关性，三序列平方值的自相关性也很强，说明存在ARCH效应，图1为变量序列图。

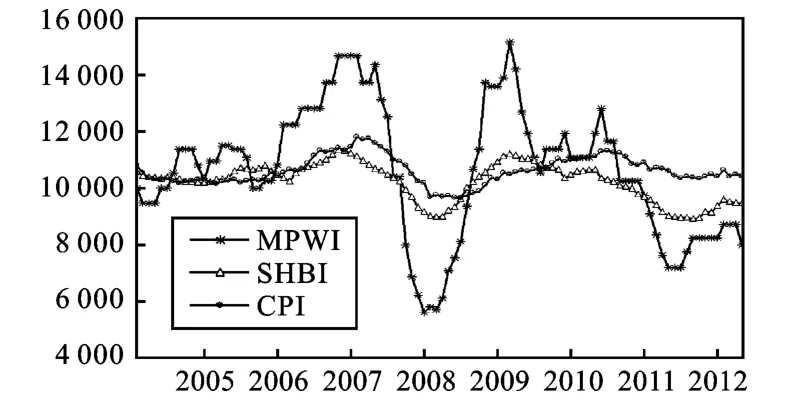
图1 变量序列图

四、实证分析

（一）相关检验与VAR模型估计

1．单位根检验。进行时间序列分析前需要进行序列ADF单位根检验，表1倒数第二行显示在10%水平上MPWI和SHBI拒绝包含单位根的原假设，但在1%水平上接受包含单位根的原假设，CPI序列在10%水平上接受包含单位根的原假设，对三个序列进行一阶差分后再次进行检验，发现三个序列的一阶差分序列均在1%水平上拒绝存在单位根原假设，故认为△MPWI、△SHBI、△CPI序列平稳，即三个变量为1阶单整序列（详见表1）。

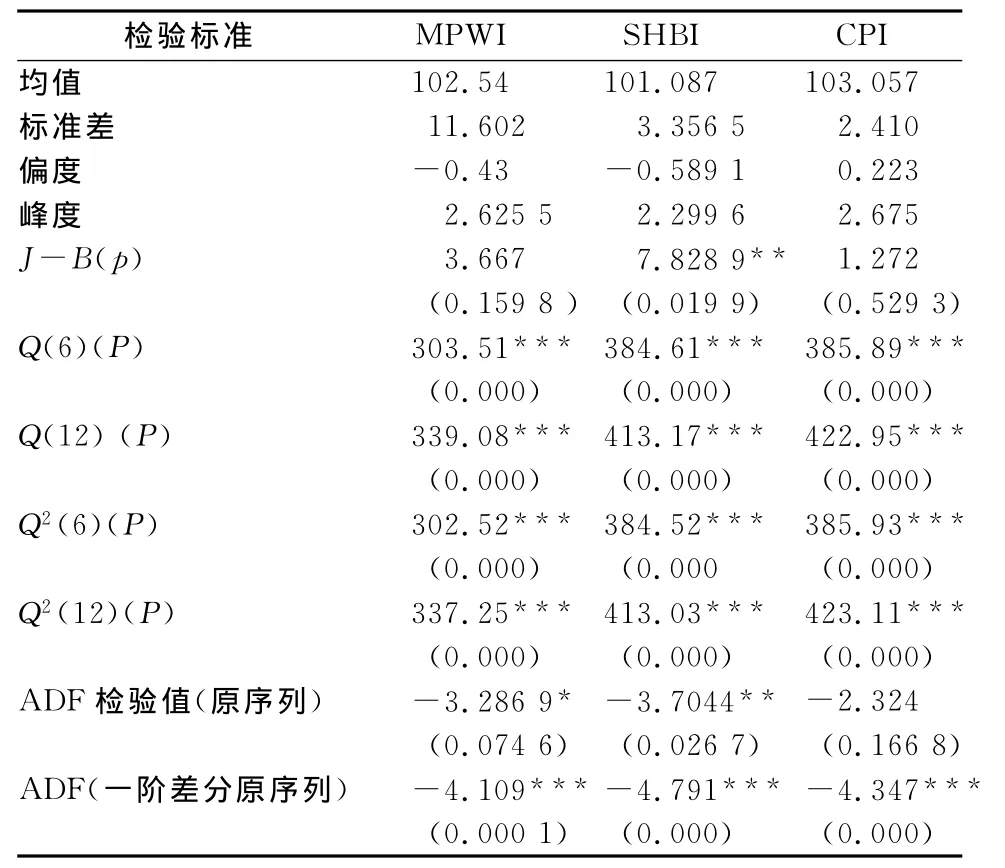
表1 描述性统计与相关检验表

2．协整检验。在检验出变量序列存在同阶单整后，需要考虑变量间的长期均衡关系。可以采用EG两步法进行考察，相比EG法而言Johanson协整检验不仅能够对协整关系存在与否进行检验，还能够得出具体协整关系的个数。进行协整检验之前，需要构建向量自回归模型（VAR）和确定VAR模型的滞后阶数与稳定性，根据滞后结构模块中的“Lag length criteria”功能进行滞后检验，其中最终预测误差（FPE）、赤池信息（AIC）、汉南昆信息（HQ）认为滞后3阶最佳，施瓦茨信息（SC）认为滞后2阶最佳，根据多数原则确定滞后阶数为3。根据AR特征多项式的根的检验发现特征根倒数的模都在单位圆内，故认为VAR模型稳定（详见图2）。Johanson协整检验有五种方式，本文给出了各种方式下的检验结果（见表2），五种形式的检验均显示变量间存在协整关系。

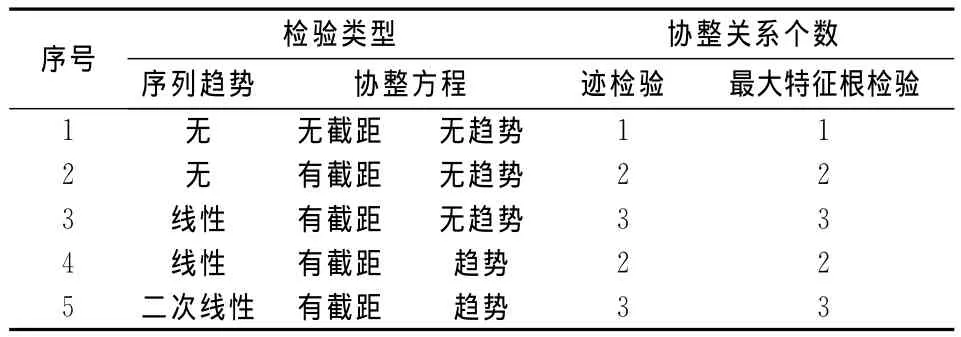
表2 Johanson协整检验表

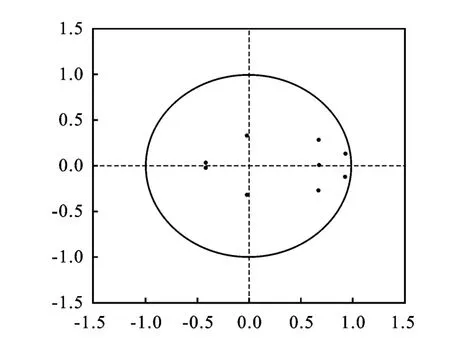
图2 AR特征多项式的根检验图

3．VAR（3）估计。滞后3阶的VAR估计结果如表3所示。在经济预警指数方程中，其自身滞后1和3期的系数非常显著但方向不同，说明该指数存在序列自相关性，国房景气指数和CPI指数的滞后期对当期MPWI指数影响较为显著；在国房景气指数方程中，其自身滞后1、2期值对当期值存在显著影响，说明存在序列相关性，经济预警指数和CPI指数的滞后1期对SHBI指数当期值没有影响，但两个序列的滞后2、3期值对SHBI指数当期值有显著影响；在CPI指数方程中，CPI自身滞后1、2期值对当期值有显著影响，存在序列相关性，而国房景气指数的滞后期值对CPI当期值无显著影响，经济预警指数的滞后1期值对CPI指数当期值有显著影响。但在理论界通常认为VAR模型是一套缺乏理论基础、仅基于统计性质的模型，所以在进行解释时并不依据估计系数，而是通过设置随机误差项的一个冲击（脉冲）来进行脉冲响应分析，以揭示变量间长期动态关系特征。因为本文主要目的是为了得到VAR模型的残差－协方差信息从而测算各指标间的波动溢出效应，所以并不进一步进行脉冲响应分析和方差分解。

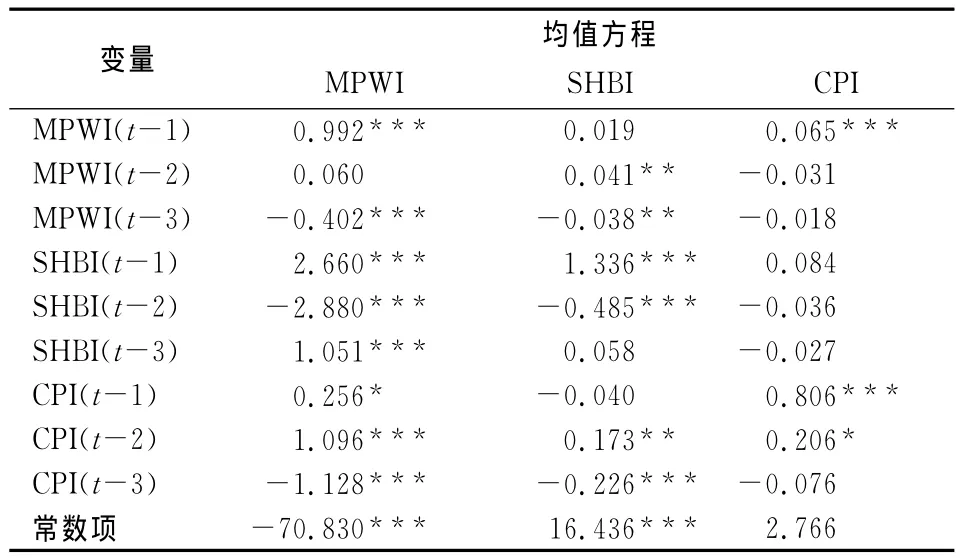
表3 VAR（3）模型估计结果表

（二）GARCH－BEKK估计结果与波动溢出检验

在进行VAR均值方程估计得到了条件残差的方差－协方差矩阵后，对公式（2）表示的GARCHBEKK模型采用 Winrats8．0软件进行估计。采用BFGS算法的估计结果如表4所示。有以下结论：一是A代表的 ARCH 效应矩阵中A（1，1）、A（2，2）估计系数均在1%水平显著为正，说明经济预警指数、国房景气指数波动存在ARCH效应，自身当期波动受到了前期残差平方的影响，A（3，3）估计系数为正但不显著，说明CPI序列波动不能存在ARCH效应；二是GARCH效应矩阵B中对角线元素B（1，1）、B（2，2）的估计系数在1%水平显著，说明MPWI和SHBI序列存在显著的GARCH效应，即自身滞后期波动对本期波动有正向作用，即大的波动后面跟大的波动，小的波动后面跟着小的波动，CPI指数的GARCH效应不显著，其自身滞后期波动对本期波动无显著影响；三是B矩阵中非对角元素B（1，2）和B（3，2）显著异于0，说明国房景气指数波动受到了来自经济预警指数和CPI指数滞后波动影响，A矩阵中A（3，1）和A（3，2）估计系数显著异于0，说明CPI指数的前期残差平方对当期经济预警指数、国房景气指数波动有显著影响。

表4 GARCH－BEKK估计结果表

如果某一个指数对另外一个指数的波动溢出效应显著，意味着在方差方程中的矩阵A、B对应的非对角线元素的联合系数应当显著不为零。例如考察经济预警指数对国房景气指数的波动溢出效应显著与否，只需检验A（1，2）和B（1，2）估计系数的联合显著性。波动溢出检验结果显示（见表5）：经济预警指数对国房景气指数存在着显著的波动溢出效应（5%水平上拒绝原假设），但经济预警指数对CPI指数的波动溢出效应不显著；国房景气指数对经济预警指数和CPI指数的波动溢出效应在10%水平上不显著；CPI指数对国房景气指数和经济预警指数在1%水平上有显著波动溢出作用。说明经济预警指数和国房景气指数对CPI指数不存在波动溢出效应，相反CPI指数对经济预警指数和国房景气指数的波动溢出效应较为显著，所以控制中国经济系统的短期外部风险，稳定物价、有效控制通货膨胀是维护中国经济稳定的重要举措。经济预警指数和国房景气指数之间存在着从前者到后者的单向波动溢出关系，因为一些随机外部冲击（如金融危机爆发）使经济系统意识到了风险的存在，从而通过产业链机制会将经济风险信号传递给地产业。但相反的关系却不存在，即国房景气指数对经济预警指数不存在波动溢出效应，体现了后者对前者波动的不敏感，因为投机行为掩盖了房地产的真实需求，房价虚高没有作为一种风险体现在预警指数上。

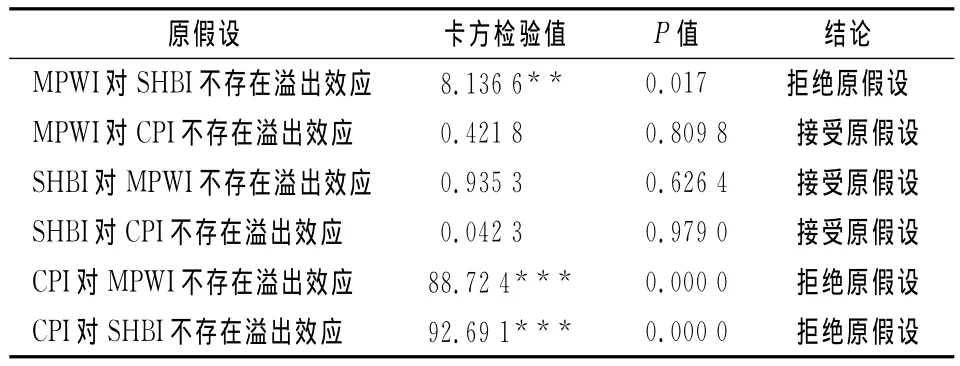
表5 波动溢出检验表

五、总 结

根据全文的分析结果，发现中国经济预警指数、国房景气指数存在较为显著的波动集聚性（ARCH效应和GARCH效应），即滞后波动和滞后残差平方对当期波动有显著影响，但CPI指数波动的ARCH效应和GARCH效应不显著。经济预警指数和CPI指数对国房景气指数存在着较强的波动溢出效应，即国房景气指数波动不仅受到自身前期波动与前期残差平方的影响，还受到其他指标前期波动和残差平方的影响；CPI指数对经济预警指数也存在着显著的波动溢出效应，但国房景气指数对经济预警指数和CPI指数波动无显著波动溢出效应。

根据以上结论，建议如下：1．国家控制通胀、维护房地产业平稳有序发展和维持经济系统稳定的举措应当具有协同效力，尽力避免“脚痛医脚、头痛医头”的分割控制模式，尤其是要关注物价指数波动会加剧国房景气指数和经济预警指数的波动。2．本文分析的三个指数间的绝对冲击体现了各指标间的动态影响关系，包括影响的方向与程度，但是指标间的波动影响更应该受到关注，因为风险传递是一个系统行为，学术界应当侧重于经济指标间的波动影响分析并提出可行的对策，尽可能避免经济指数大起大落震荡剧烈；3．不同经济主管部门应当加强信息沟通和进行协同机制建设，共同抵制风险，在经济紧密化和产业协同度越来越高的当今时代，任何一个经济部门都不可能独立于其他部门单独有效的完成自身的调控任务，所以各行业主管部门应紧密合作，促使中国经济快速、健康、有序发展。

［1］ 姚小剑．我国经济增长与物价波动关系分析［J］．西安石油大学学报：社会科学版，2008（3）．

［2］ 孔繁龙，道加华旦．通货膨胀与经济增长之间关系的实证分析［J］．西藏大学学报：社会科学版，2009（2）．

［3］ 张勇，闫鹏，杜子平．我国房地产业发展与宏观经济关联性研究［J］．建筑经济，2010（1）．

［4］ 位志宇，杨忠直，王爱民．房地产价格与宏观经济基本面研究的新视角［J］．系统管理学报，2007（5）．

［5］ 强林飞，贺娜，吴诣民．中国银行信贷、房地产价格与宏观经济互动关系研究——基于VAR模型的实证分析［J］．统计与信息论坛，2009（9）．

［6］ 孟彩云，王聪．房地产价格、泰勒规则与宏观经济调控——基于2000－2010年我国宏观经济数据的检验［J］．当代财经，2012（2）．

［7］ 黄飞雪，金建东．金融危机前后中国房价指数对CPI的影响［J］．经济数学，2010（3）．

［8］ 汪小亚，代鹏．房地产价格与CPI相关性：实证分析［J］．中国金融，2005（2）．

［9］ 范万志，李海海．房地产价格波动，通货膨胀与收入分配差距［J］．青海社会科学，2010（3）．

［10］王新军，赖敏晖．沪、深、美股市之间波动溢出关系研究——基于三元BEKK－GARCH（1，1）模型［J］．山东社会科学，2011（11）．