基于分形理论的区域经济差异分析——以河南省为例

李佼瑞，徐书雅

（西安财经学院 统计研究院，陕西 西安710100）

一、引 言

区域经济差异及其变化是改革开放以来中国经济和社会发展中倍受学术界、政府和广大民众关注的一个重大问题。区域经济发展不平衡的失控是社会和谐及协调发展的重要障碍。

近年来，越来越多的学者开始运用不同方法从不同的角度来研究中国和各个省、市、地区的区域经济差异。国内许多学者采用威廉姆系数测度区域经济差异的变动趋势，也有许多学者从多元统计分析的角度通过构建指标体系来考察区域经济发展的差异，其中衡量收入分配差异程度较为常用的代表性指标还有洛伦茨曲线、基尼系数、库茨涅茨系数等。综合比较几种方法，学者认为库茨涅茨系数是描述地区间不平衡性指标中比较直观的一个，同时该系数不仅计算方便，还可以通过适当的分解，进一步揭示经济增长不平衡变化的原因。所以，本文从库茨涅茨系数的角度对河南省区域经济增长差异的变动情况进行实证分析。另外，随着动力系统理论在经济中越来越广泛的应用，混沌思想下的“分形”也越来越多的被应用在城市研究中。例如，沙里宁提出了著名的有机疏散理论，克里斯塔勒应用分形理论提出不同级别的城市呈现自相似的六边形网络，刘继生、陈彦光、岳文泽等人将分形理论应用于城镇体系的规模结构、空间相互作用、中心城市吸引力等研究领域［1－3］。本文在实证分析的基础上运用分形方法进一步对河南省的区域发展差异进行分析，从而从分形的角度来考察其差异的主要原因，并提出一些可行性的建议。

二、区域经济差异的实证分析

为了客观而全面地说明地区经济差异的时空分布特征，本文引入库茨涅茨系数来描述河南省区域不平衡性的经济现状。库茨涅茨系数又叫相对收入阶层分布，它代表一定收入水平下的阶层所占的比重，是反映收入分配平均程度的指标［4］。库茨涅茨系数的计算公式如下：

其中，pi与qi分别表示第i个地区的人口与GDP占全省的比重，k表示库茨涅茨不平衡系数，n代表研究的样本空间。将 （pi－qi）从大到小排列之后，必然存在这样的一个m值，使得当i#m时，pi－qi≥0，为低收入人群人口比例与经济比例之差；当i＞m时，pi－qi＜0，为高收入人群人口比例与经济比例之差。将式（1）分解为：

从式（3）中可以看出，k的值可以分解成两部分，其中A表示低收入人群人口的相对变化所导致的k值的变化，其数值越大，表明低收入人群的人口对地区的经济差异影响越大；B表示由于高收入人群收入变化导致k值的变化，同样的，其数值越大表明高收入人群的收入扩大了区域之间的经济差异。这就为我们提供了解释区域发展不平衡性动态变化的原因，也为减小区域发展不平衡性提供了途径。同时，m值越高，表明人力资源生产效率低下的区域个数也就越多。河南省各地区人均GDP的库茨涅茨系数及其分解结果见表1、图1。

表1 河南省人均GDP的库茨涅茨系数及其分解表

图1 河南省区域发展不平衡性变化及其分解图

一般来说，随着经济的长期发展，由于地区间产业结构的不平衡性、资源禀赋、技术研发能力、区位交通条件、社会经济基础、国家政策、获得信息的多少以及速度的快慢差异等因素的影响，各区域之间的经济增长差距会逐渐扩大。从上面对库茨涅茨不平衡系数k的分析结果也可以进一步发现，除了2003年、2010年有些特殊情况外，长期以来，河南省区域经济增长不平衡的加深，导致的结果是低收入人群占总人口的比重下降与高收入人群占总收入的比重增加，对k的影响开始逐步增强。

从图1可以看出，2000年、2003年低收入人群的人口比重均有明显上升，2003年上升幅度尤其大，不过高收入人群收入比重也明显下降，所以总体不平衡性并没有出现明显的变化，同时库茨涅茨系数所表明的总体不平衡性在1999年至2009年总体来说呈现平稳的增长趋势，但是在2010年，低收入人群的人口比重又出现了一个明显的上升点，而高收入人群的收入比重也出现了一个明显的下降点，并且上升的程度大于下降的程度，使得总体的不平衡性略有下降。

三、区域经济增长差异发展趋势的分形分析

自20世纪60年代以来，混沌理论被迅速应用到了包括自然科学与社会科学在内的众多学科领域。城市是一个典型的混沌系统，混沌理论所揭示出的非确定性与不可预测性、有序与无序等属性，为我们从混沌理论的角度对城市区域经济的发展进行分析提供了一个新的视角［5］。

由图1可以看出，库茨涅茨曲线是一种不连续的曲折线段，这种非光滑、不可微分的分形曲线，用经典数学方法处理起来会稍显困难，但分形理论却是解决这种难以描述复杂问题的一种有效理论方法，并且自相似性是分形最重要的特征，我们可以通过分维数来定量的描述分形。另外，从上一部分的分析中可以清楚地看到，河南省各区域的经济增长确实存在着显著的差异，并且该部分的分析是从河南省的全局角度考虑的。众所周知，河南省是一个农业大省，农业人口占有很大比重，本文将尝试从其反面的角度，即非农业人口的角度来考察其经济发展的差异性。幸运的是，分形理论中的Ziff维数正是从城市人口规模的角度进行研究的，从而我们可以采用城市地理学中的规模分布方法和分形维理论，从河南省城市体系的角度来分析其经济发展的差异性，以期为河南省城镇体系空间结构优化及缩小其差异的研究提供有益的借鉴。

（一）城市体系等级规模结构的分形理论

城市规模分布是指某区域（国家、地区）内各级城市人口规模的层次分布［6］。理论上讲，每个地区内都会存在不同规模的城市，如果按照不同的人口划分尺度，就会有不同的城市个数。现在的许多研究已经证明了区域城市体系规模分布具有分形特征［7］，并且证明了罗卡特模式一般化中的参数q和帕累托（Pareto）分布中的参数b具有分形维数的意义，因此，利用参数q和b的变化分析河南省城市体系规模结构状况在理论上具有一定的可行性。

将罗卡特模式对数化之后与帕累托分布的对数化形式进行比较可以发现两个模式的实质是相同的，并能得到结论：b＝q－1。其中b为帕累托对数方程式的系数，即Pareto系数，q为位序－规模分布斜率，即Ziff维数。

美国数学家 Mandelbrot B B在20世纪70年代中期创立了分形理论（Fractal Theory），认为那些外在不规则的几何体（或者现象）有着自己内在的规律性和自相似性，并按照内在的规律发展演化［8］。Mandelbrot把这种部分与整体以某种方式相似的形体称为分形体，并且分形体的自相似性是统计意义上的自相似性，而不是数学意义上的自相似性。由于分形体不具备特征尺度，因而它难以用通常的数学尺度来度量，所以通过分形维数（fractal dimension，简称“分维”）等主要特征参数来描述分形体。计算分形维数的方法有拓扑维、容量维、相似维和关联维等，而在描述城市的规模分布时常用的是豪斯道夫维数（Hausdorff dimension）D，其表达式为：

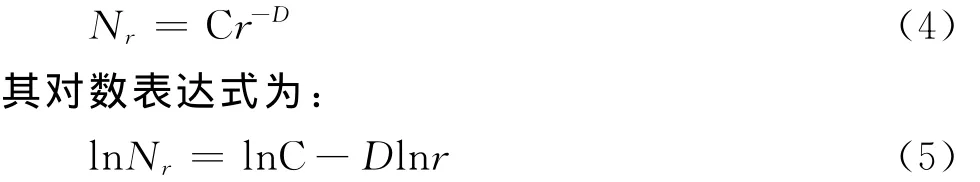
其中r为所选择的测量尺度，C为常数，D为豪斯道夫维数。

由豪斯道夫维数与等级规模分布公式类比可知，等级规模分布服从幂定律，因而具有分形特征，因此也验证了罗卡特模式和帕累托分布中的参数b和q具有分维的意义，同时将式（5）与帕累托分布和罗卡特模式相比较可知：D＝b＝q－1。

研究表明，当D＝q＝1时，最大城市与最小城市人口数量的比值为整个城市体系的城市数目，这是自然状态下的最优分布；当q＜1，即D＞1时，城市体系的人口分布比较均匀，城市规模分布比较集中，此时中间位序发育较快；当q＞1，即D＜1时，城市体系的人口分布差异较大，城市规模分散，此时首位城市的垄断性较强；当D→!，即q→0时，区域内所有城市一样大；当D→0，即q→!时，区域内只有一个城市。后两种是理论分析的极端情况，现实中一般不存在，因为一个区域内城市体系的演化受经济、政治、社会、自然等诸多因素影响，各因素综合作用必将导致城市规模的差异［6］。

（二）城市体系等级规模结构分形研究

1．河南省城市体系等级规模分布的现状分析

从第一部分的分析中我们知道，河南省现有18个市，本文参考中国划分城市人口规模级别的标准，将城市共分为5个等级：第一级为超大城市，城市非农业人口规模大于200万；第二级为特大城市，其人口规模为100万～200万；第三级为大城市，其人口规模为50万～100万；第四级为中等城市，其人口规模为20万～50万；第五级为小城市，其人口规模小于20万。根据上述划分标准，本文在分析中使用市区非农业人口作为城市规模的特征量，对河南省18个市的规模体系进行现状分析，得到河南省城市体系规模级别构成（表2）和河南省城市市区非农人口排序（表3）。

表2 河南省城市体系规模级别构成表

表3 河南省城市市区非农人口排序表

从表2可知，从市区非农业人口的角度考虑，河南省城市体系的规模结构比较集中，18个城市中超大城市所占的比重仅为6%，其非农人口占所有非农人口的13%，而特大城市和大城市所占数目比较多，其比重之和占总的城市数量的89%，并且规模也较大，其市区非农人口占所有城市非农人口的86%，但是中等城市及其规模以下的小城市数目则比较少，且其规模也比较小，6%的城市非农人口的比重仅为1%。以上分析充分说明，河南省城市人口分布较为集中，主要分布在数目较多的特大城市和大城市，中小城市数目较少，且规模较小。

从表3可知，各个等级城市之间的规模相差也比较大，这种差距在超大城市与其以下规模城市之间尤其明显。城市体系等级规模失衡，使得相邻等级的城市间的信息、产业、技术、劳动力、资金等都不能很好地流动，从而不能对超大城市郑州的信息、产业、技术、劳动力、资金等起到分流作用。由于中小城市的基础设施相对薄弱，资金、技术缺乏以及第三产业不发达等因素造成经济发展受到限制，不能直接接受较高等级城市产业转移和辐射的带动作用，同时中小城市辐射与带动作用较弱，不能吸入更多劳动力，无法减轻较高等级城市的人口压力。

2．城市体系等级规模结构的分形分析

由于城市规模体系的值与豪斯道夫维数的值具有反比关系（D＝b＝q－1），因此，通过计算q值就可以得到D值［9］。以2009年的数据为例，首先对城市人口规模进行排序，然后将点（Ri，Pi）对数化（lnRi，lnPi）（见表4），通过建立一元线性回归模型，可以求得Ziff维数，即q值，进而可以算出豪斯道夫维数D。通过表3的数据可以得到双对数曲线图（图2），然后按照上述分型理论，计算可知Ziff维数q为0．508 8，R2为0．837 2，从而 Hausdorff维数D＝1／q＝1．97。用同样的方法分别算出其它年份的Ziff维数、相关系数和Hausdorff维数D（表5）。

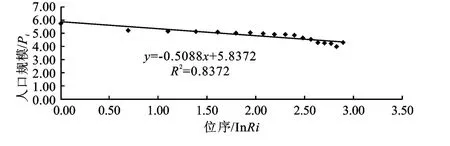
图2 2009年河南城市体系规模序列双对数散点图

表4 河南省18个城市1999年至2009年的q、R2和D表

从表4可知，相关系数R2值均达到0．822 1以上，相关性比较好，即拟合效果较好，说明河南省城市体系的等级分布确实具有分形特征，可以用分形理论进行分析。从分析结果可知，1999年至2009年，河南省城市体系规模分布的Ziff维数q值均小于1，其分维数D均大于1，说明高位次城市规模不是很突出，城镇规模分布较为集中，人口分布比较均衡，但是由于高位次城市的首位作用较弱，其带动区域经济发展的作用有限。另外从分维值的变化可以看出，11年来，分维值先变小后变大，说明城市规模分布的分散和集中的力量相互交织，但是2007年之后有一个明显的上升趋势，这说明城镇规模分布的集中力量大于分散力量，高位次城市的首位作用有所提高。根据城市体系规模结构发展阶段理论可知，目前河南省城市体系最大城市的首位作用比较弱，虽然在大城市的影响下有了一定程度的提高，但是其影响力距理想状态仍有一定的差距，属于发展的中间阶段，尚未形成理想的规模序列结构，从而需要进一步的整合设计。

四、结论与建议

从对河南省近十多年来的整体均衡性分析和局部的城市规模体系的分形分析可知，河南省区域之间经济发展存在较大的差异，并且其城镇体系空间结构存在分形特征，城市体系的最大城市影响力不够，中间位序城镇数目较多，小城市规模发育水平较低，正处于发展的中期阶段，离理想的规模结构仍有较大的差距。针对以上特点和问题提出以下建议：

首先，培养中心城市的辐射扩散能力。郑州市作为河南省最大的和省会城市，其城市首位度不够突出，带动辐射作用不是很充分，没有形成成熟的城市体系规模结构，因此需要进一步发挥其带动作用，增强核心竞争力，积极构建郑州都市圈，使其成为真正的首位城市。

其次，加强重点城市建设，完善城市体系规模结构。针对河南省城市体系中间序列城镇数目较多、小城市低水平发育这一现状，可选择基础条件较好、发展潜力大的特大城市和大城市重点培育，从而促进郑州的辐射带动作用。另外，研究城镇体系空间结构的同时也不能忽略其历史因素［10］295－298，可以考虑从细胞自动机（CA）模拟技术的角度研究区域城市化发展的历史进程，然后借助混沌理论等分析工具进一步揭示其系统演化的动力学特征和分形结构的发展机制［11－12］，从而可以从开封、洛阳、安阳等一些历史古都中筛选出培育对象，重点加强培育。

［1］ 陈彦光，刘继生．城市规模分布的分形和分维 ［J］．人文地理，1999（2）．

［2］ 刘继生，陈彦光．城镇体系空间结构的分形维数及其测算方法 ［J］．地理研究，1999（1）．

［3］ 岳文泽，徐建华，司有元，等．分形理论在人文地理学中的应用研究 ［J］．地理学与国土研究，2001（2）．

［4］ 吴殿廷，宋金平，梁进社，等．库茨涅茨比率的分解及其在我国地区差异分析中的应用 ［J］．地理科学，2003（8）．

［5］ 徐岩，宋伟轩．混沌理论对城市规划的启示 ［J］．规划师，2012（4）．

［6］ 刘继生，陈彦光．东北地区城市规模分布的分形特征 ［J］．人文地理，1999，14（3）．

［7］ 刘继生，陈彦光．城市规模分布的分形和分维 ［J］．人文地理，1999，14（2）．

［8］ 邢海虹，刘科伟．基于分形理论对陕西城市体系等级规模分布研究 ［J］．人文地理，2007，22（4）．

［9］ 刘继生，陈彦光．城镇体系等级结构的分形维数及其测算方法 ［J］．地理研究，1998，17（1）．

［10］周一星．城市地理学［M］．北京：商务印书馆，1995．

［11］Clarke K C，Hoppen S，Gaydos L．A Self－modifying Cellular Automaton Model of Historical Urbanization in the San Francisco Bay Area［J］．Environment and Planning and Design，1997，24（2）．

［12］Sanders L，Pumain D，Mathian H，et al．SIMPOP：A Multiagent System for the Study of Urbanism［J］．Environment and Planning B：Planning and Design，1997，24（2）．