典型相关分析的延拓研究

杜子芳，常志勇，2

（1．中国人民大学 统计学院，北京100872；2．河南科技大学 数学与统计学院，河南 洛阳471023）

一、典型相关分析概述

在两个随机向量之间的建模问题中，逻辑上，只有在两个随机向量之间存在关系的基础上，才能建立这两个随机向量之间的定量模型。两个随机向量之间关系的统计刻画就是典型相关分析。典型相关分析是随机向量之间建模问题的前奏，在多元统计建模中发挥着至关重要的基础作用。

设两个随机向量分别为

X＝ （X1，X2，…，Xp）′

Y＝ （Y1，Y2，…，Yq）′

（不失一般性，设p＜q）

寻找适合的系数向量

a＝ （a1，a2，…，ap）′和b＝ （b1，b2，…，bq）′

使得由此生成的线性组合对

U＝a′X＝a1X1＋a2X2＋…＋apXp

V＝b′Y＝b1Y1＋b2Y2＋…＋bqYq

拥有最大的相关系数［1］。

由拉格朗日乘数法求得，共有k≤min（p，q）组典型相关变量，每组典型相关变量的系数向量a＝（a1，a2，…，ap）′和b＝ （b1，b2，…，bq）′为对应于同一个特征值λ2的特征向量。

在实际场合，以下指标都可用来衡量两组数值型随机向量的相关关系［2］315－322，并统称为广义相关系数。

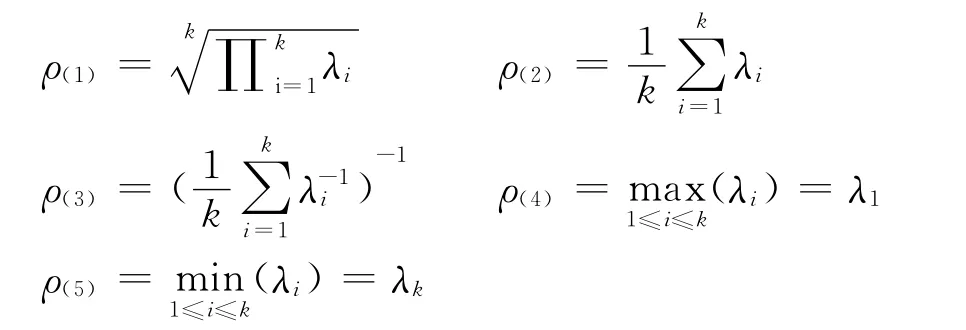
在广义相关系数中，可以证明：ρ（4）是偏大的，ρ（5）是偏小的，另外三种是适中的。依一般思维惯性，极容易产生适中的比较有代表性因而更有价值的结论，但在典型相关分析中，极值更有价值。因为典型相关分析是其他多元统计分析的前奏，若广义相关系数特别是那些本身偏大的广义相关系数不高，则说明因变量组与自变量组之间肯定无法建立起有效的因果模型；反之有可能建立起有效的因果模型。同理，若广义相关系数即使是那些本身偏小的广义相关系数都很高，则说明因变量组与自变量组之间有可能（但并无把握）建立起有效的因果模型。

二、卡方检验确定典型相关变量个数的弊端

典型相关分析中，部分教程和论文使用巴特莱特（Bartlett）的χ2检验确定典型相关变量的个数［3］539－574，［4］。χ2检验的过程为

依次进行下去，直至到第l（l≤k）个典型相关系数λl检验为不显著或所有典型相关系数都通过检验时停止。

从上述分析过程中，可知Bartlett检验仅使用了典型相关变量之间的相关性。从（X，Y）协方差矩阵的角度看，Bartlett检验仅使用了该协方差矩阵的右上角分块阵（或斜对角元素）的信息，而没有使用对角线元素的信息。典型相关变量仅是原变量的线性组合，可能存在不同的线性组合系数使得线性组合的结果一样，但不同的线性组合系数所携带的信息量不同。因此，仅从典型变量之间的相关性的角度出发来确定典型相关变量的个数有待改进。同样Rao给出的F检验，在小样本的情况下，检验的功效比χ2检验的功效高［5］582－587，但也仅是检验典型相关变量之间的相关性。

三、典型相关变量个数确定方法的改进

Stewart和Love也注意到了这个问题，考虑到典型相关分析中两个随机向量维数不同的问题，定义了冗余分析（redundancy analysis）［6］。该方法使用典型相关变量与原始随机向量之间的相关系数构造典型变量代表性的度量（已在SPSS和SAS软件中模块化）。其基本原理：

记rl＝ρUl，Vl，定义

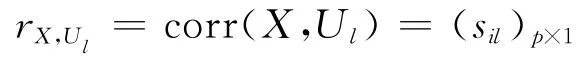
冗余分析从原始变量与典型相关变量之间的简单相关系数出发判定典型相关变量的个数。典型相关变量与原始变量之间的相关系数取决于两个因素：典型相关变量表达式中的系数和变量组中某一个变量与另一个变量组的简单相关系数。这两种系数在计算线性内积时会存在由于符号而使得值相互抵消的情况。而冗余分析仅从相关系数的角度对组间变量的相关程度进行分析，不能如实反映实际情况。因此，该方法有待改进。Hair等也指出冗余分析是一个有争议的方法，但是没有给出改进的方法［7］245－249。

以下将给出一种改进冗余分析的算法。从典型相关变量的求解过程中，可知各个随机向量的典型相关变量具有主成分的性质。所以，考虑使用主成分的方差贡献率，研究该典型相关变量对原变量的代表性。典型相关分析的关键在于数值型变量的线性组合，故其应用场合与主成分分析及因子分析最为相似，理想的应是同组变量计量单位与量纲都一致，且其系数最好都是1或0，这样有益于人们识别和理解典型相关变量（原变量线性组合）的实际意义。由于相关系数具有线性不变性（两个变量的相关系数与其各自的任一线性组合间的相关系数相等），将线性组合中某一线性系数调整为1是可行的。

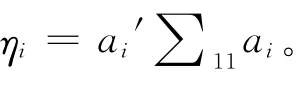
选择累计贡献率的方法主要有三种：一是根据专业而非统计的考虑而定，二是取一个较大百分比的累积贡献率（例如80%，85%，90% 之类的百分数）所对应的典型相关变量数目。不过第一种方法虽然合理，却不易操作，尤其是在程序编写上，不易确定阈值。如果对原始变量先标准化，则

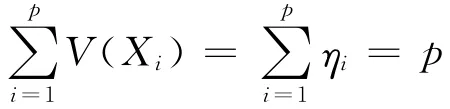
因此ηi的均值为1，于是提取的前几个典型相关变量的贡献率理应高于所有的均值，其相应特征根满足η≥1的条件就顺理成章了。因此，以η≥1作为提取阈值的第三种方法更为常见。

在典型相关分析中，确定典型相关变量的个数时不仅要考虑典型相关变量之间的相关性的强弱，而且也应该考虑典型相关变量在因变量组或自变量组的代表性。从统计意义上看，只有当典型相关变量既满足较强的相关性，又能携带大量的原向量组的信息时，才是一组较好的典型相关变量［8］。从数学的角度看，该问题应该是一个多目标最优化问题，而非单目标最优化问题。

四、典型相关变量中的变量选择

余下的问题是如何在自变量组与因变量组内部进行变量选择，以便构建模型。“世界万物是有联系的”，当变量组的维数增加时，变量之间的相关性会增加。在建模时，需要在模型的复杂度和信息量之间进行均衡。或者在一定的复杂度下使尽可能多的信息进入模型，或者在信息量一定时，使模型尽可能的简化。因此，在确定了典型相关变量的个数后，使每个典型相关变量成为尽可能少的原始变量的线性组合，是在信息量一定时模型尽可能简化的思路的实现。同时在模型简化后，可使得对典型相关变量的现实意义的解释更加清晰。

变量选择的准则有几个合乎逻辑的线索，一是根据线性组合中的线性系数大小，大者进，小者出；二是以因变量线性组合中的前几个最大线性系数所对应的因变量为主线，将与这些因变量相关程度最高的自变量列入最终保留自变量的名单；三是使用典型相关变量解释各个原始变量方差的程度。

上述三种选择方法中，前两者相对易实现，下面给出第三种方法的具体实现过程：

设提取的k个典型相关变量的系数矩阵分别为

如果hxi越大，则X中第i个分量对本组典型相关变量的影响程度越大。同理，hyj越大，则Y中第j个分量对本组典型相关变量的影响程度越大。从而可据此对典型相关变量中的原始变量进行选择。

五、数据实例

为研究人的上肢和下肢之间的关系，对成年男子的身高进行测量，数据单位为毫米（mm）。用来反映上肢长度的测量数据：上臂长（shb）＝肩高－肘高，上肢长（shzh）＝肩高－中指指尖高，上肢前伸长（shzhsh），前臂加手前伸长（qb）等四组数据；用来反映下肢长度的测量数据：会阴高（hy），胫骨点高（jg），坐姿膝高（zzx），臀膝距（gxj），坐姿下肢长（zzxz）等五组数据。从中国第一次成年人工效学基础参数调查的数据中随机抽取上述变量的1 000组观察值。使用SPSS和R软件进行数据的处理与分析，首先使用SPSS中的CANCORR过程对数据进行典型相关分析；然后使用R软件完成本分析中的其他部分。实例分析的主要目的在于将本文中方法的结论与SPSS中的结论进行对比。

利用SPSS软件对该数据集进行典型相关分析。将上肢数据的相关系数矩阵、下肢数据的相关系数矩阵及两组数据的相关系数矩阵（两组数据集标准化后的协方差阵）等三个矩阵整理为表1，计算各对典型相关变量的相关系数，见表2。

表1 相关系数矩阵表

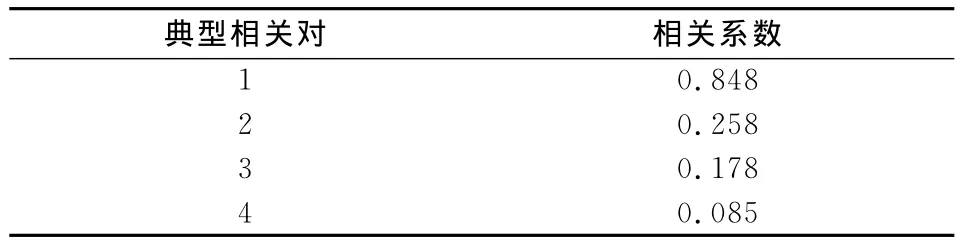
表2 典型变量的相关系数表

表3 广义相关系数表

由表3可见，最大的相关系数比较大，因此可能存在相关关系。但几何平均，算术平均与调和平均的值都不大，因此此类系数的作用相对较弱。

SPSS软件中使用卡方检验检验典型相关系数的显著性，其检验结果见表4。

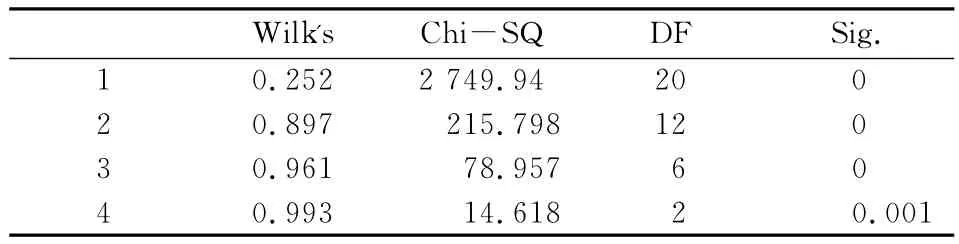
表4 相关系数的卡方检验表

在显著性水平α＝0．05下，四对典型相关变量都通过卡方检验，但并不意味着可以使用四对典型相关变量进行后续建模。

为了研究典型相关变量对所在组的解释能力，分别使用冗余分析中的组内方差比和本文提出的方差贡献率进行计算，并将计算结果使用极限作为评价标准，结果汇总为表5。

表5 典型相关变量对所在组变量的方差解释表

根据表5中数据，无论采用本文提出的累积贡献率较大还是采用n≥1的标准，都得到一致的结论：选择第一对典型相关变量具有较好的代表性。这与冗余分析的结果一致。但是本文所提方法给出的方差比例的离散程度比SPSS中给出的方差比例的离散程度大，从而在选择典型相关变量个数时相对有效。

在确定典型相关变量的个数后，选择典型相关变量表达式中原始变量。依据第四部分中给出的三种方法，分别给出其选择过程。由于第一种方法和第二种方法中都需要用到典型相关变量的表达式，故首先计算该表达式（见表6）。同时，计算第三种方法中需要的各个分量对典型相关变量的共变度（见表7）。

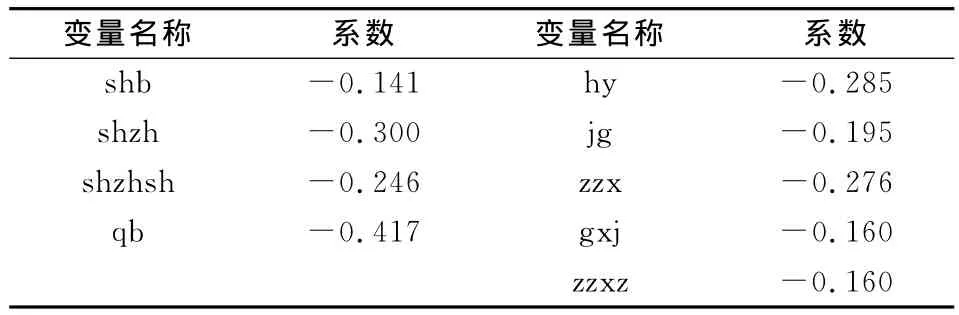
表6 典型相关变量表达式表

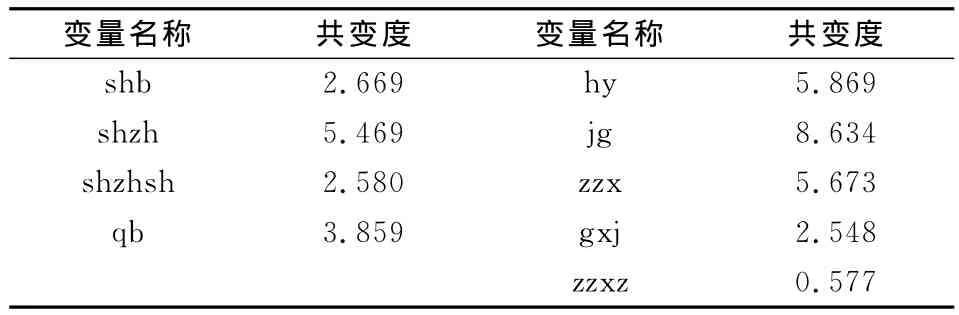
表7 原始变量的共变度表

但对于统计意义上的“大小”有多种不同的定义方法和判断标准，考虑到表达式中，系数的符号问题，本文使用绝对值的均值作为评价标准。即，如果某数据的绝对值小于所在组所有数据绝对值的均值，则认为该数据“小”，否则，认为该数据“大”。

采用第一种方法。从表6中可知：上肢数据组各系数绝对值的均值为0．276，故依据上述标准保留shzh和qb两个变量；下肢数据组各系数绝对值的均值为0．215 2，故保留hy和zzx两个变量。

对于第二种方法，假定下肢向量组为因变量，上肢向量组为自变量。首先计算下肢变量组的第一个典型相关变量的表达式，其线性组合表达式中，系数比较大的为hy和zzx两个变量。所以，在下肢向量组中保留这两个变量，剔除其他变量。然后，在原变量的相关系数矩阵（表1的右上角部分）中选择与这两个因变量相关程度较高的自变量，选择结果为保留shzh和qb两个变量。在选择时，首先分别确定与每一个因变量相关程度高的自变量。各自变量与hy的相关系数绝对值的均值为0．713 5，故与hy相关程度较高的变量为shzh和qb；各自变量与zzx的相关系数绝对值的均值为0．711 7，故也保留shzh和qb两个变量。然后对多个因变量选择的自变量集合求交集，得到自变量组应保留shzh和qb两个变量。该结果与方法一的结果相同。

在方法三中，上肢数据组共变度绝对值的均值（由于共变度的非负性，故与其均值相等）为3．644 3，故保留shzh和qb两个变量；下肢数据组绝对值的均值为4．660，故保留hy、jg和zzx三个变量。

六、结 论

典型相关分析是探索随机向量之间关系的一个有力工具，该方法大部分用于描述性分析阶段，为后续的推断分析奠定基础。因此，典型相关分析不应仅局限于寻找到典型相关变量，更应该对获得的典型相关变量进行评价。只有经过基于一定标准评价的典型相关变量才能为后续分析提供较好的基础。文中探索了如何建立评价的标准，并通过实例进行详细的分析。但也有需要进一步改进的地方，如：在变量选择时如何建立一些定量的标准；不同的选择方法之间如何衡量优劣等。

［1］ Hotelling H．Relations Between Two Sets of Variables［J］．Biometrika，1936（12）．

［2］ 张尧庭，方开泰．多元统计分析引论［M］．北京：科学出版社，2006．

［3］ Johnson R A，Wichern D W．Applied Multivariate Statistical Analysis［M］．Upper Saddle River，New Jersey：Prentice Hall，2007．

［4］ 谢琼，王雅鹏．从典型相关分析洞悉我国粮食综合生产能力［J］．数理统计与管理，2009（11）．

［5］ Rao C R．Linear Statistical Inference and Its Applications［M］．New York：John Wiley ＆Sons，Inc，1973．

［6］ Stewart D，Love W．A General Canonical Correlation Index［J］．Psychological Bulletin，1968（9）．

［7］ Joseph F Hair Jr，William C Black，Barry J Babin．多元数据分析［M］．7版．北京：机械工业出版社，2011．

［8］ Al－Kandari N M，Jolliffe I T．Variable Selection and Interpretation in Canonical Correlation Analysis［J］．Communications in Statistics－ Simulation and Computation，1997（3）．