基于分位数概率分布的动态VaR模型及其应用

杨 杰，张绍宗

（1.华南师范大学 经济与管理学院，广州 510006；2.云南师范大学 经济与管理学院，昆明 650092）

1 VaR的估计方法

VaR的常见估计方法有历史模拟法、蒙特卡洛模拟法和参数法，实践中采用较多的是参数法，其核心思想是设定金融资产或资产组合的收益率服从特定的参数分布，再通过实际数据进行参数估计，进而确定出收益率的具体分布。最后计算对应置信水平的分位数，从解出相应的VaR值。由于金融资产的收益序列常常具有尖峰厚尾的特征，因而采用参数法计算VaR时需要确定合适的概率分布来刻画这种特征，国内外很多学者正是沿着这一思路在估计金融资产的VaR值。如，Press S.在1987年提出用混合高斯分布来拟合道琼斯指数的效果比正态分布的拟合效果要好；R.N.Mantegna和H.E.Stanley（1994,1995）首次提出截断Levy分布，并将其用于美国股票和债券市场收益率的尾部拟合，实证研究显示截断Levy分布可以刻画其厚尾特征；Peter Verhoeven等（2004）用非对称t分布、非对称一般误差分布（GED）等六种分布形式代替正态分布，用于表述欧元对美元的汇率变动分布，结果表明，在描述序列的偏度、峰度以及极大似然函数值方面，前者均优于后者。国内学者的研究中，潘家柱等（2000）讨论了广义Pareto分布的性质，并利用此模型对上证指数和深证指数的收益率进行分析，给出了相应的VaR估计值；张明恒、程乾生（2002）研究了金融资产收益的混合高斯分布模型，给出了混合高斯分布的Kolmogorov-Smirnov检验方法，分析了金融资产收益的非高斯性；卢方元（2004）对上证综指和深证成指收益率分布状况进行实证分析，研究结果表明两类股指收益率均可以用稳定分布对其进行描述。

2 两类新型分位数概率模型

2.1 分位数的定义

对任意随机变量 X，任给实数τ（0＜τ＜1），若满足：P{X≤xτ}≥τ且 P{X≥xτ}≥1-τ，则称数值 xτ为随机变量X的τ分位数。这个定义在实际中由于其存在性和唯一性问题使得理论研究中发生技术上的困难，为了回避这些技术困难，统计学家将随机变量X的τ分位数定义为：

xτ=inf{x:F(x)≥τ}，τ∈(0，1)

其中，F(x)为随机变量X的分布函数。特别地，当F(x)是严增函数时，上述两种定义等价，且得到τ分位数唯一。

2.2 分位数函数

在传统的统计理论中，常常使用某种分布函数或概率密度来刻画一个随机变量的分布，其经典的代表便是正态分布。分布函数的优点在于便于计算相应随机变量的数字特征，使得人们易于掌握该随机变量的分布特征。但是，随着人们对现实数据的不断认识，发现采用分布函数来描述随机变量的分布变得越来越复杂和困难，究其原因除了分布函数的表达式变得越来越复杂外，某些随机变量的分布可能本身就不存在显式分布函数，这就使得人们开始从不同的途径来探索随机变量的分布。分位数函数的出现，就是这方面的一个有益探索。相比分布函数而言，一个随机变量的分位数函数往往具有更多优点。从广义上而言，一个随机变量的分位数函数与其分布函数呈反函数关系，两者在一定条件下呈一一对应关系，而分位数函数一般具有更为简洁的表达式，且易于数值拟合，这使得分位数分布成为近年来统计学者研究的热点之一。

2.3 两类新型分位数概率模型

下面的两类概率分布族是由蒋文江教授和邓世杰教授（2004）根据分位数的思想首先提出的，他们首先将其应用在德国证券市场上用于刻画股票收益率的分布并取得很好的效果。这里我们仍然沿用他们的表示方式来表示两类分位数概率分布族。其中，我们用QI(α，β，δ，μ)来表示第一类分位数概率分布族，其解析式可以表述为下式：

附注：模型（1）中所有的参数都具有直观的解释意义，其中μ是位置参数，δ是尺度参数，β参数的大小可以用来度量尾部的对称性，当 β=1时意味着该分布是平衡的，当 β＜(＞)1时意味着分布的右尾（左尾）比左尾（右尾）厚；参数α可以刻画分布的尾部厚度，较小的α值，意味着分布的尾部更厚。

第一类分位数概率分布族 QI(α，β，δ，μ)，具有显式分布密度，其表达式如下

其中 x∈(-∞，μ)∪(μ，+∞)，因为第一类分位数概率分布族具有显式分布密度表达式，所以我们可以直接采用极大似然估计的方法估计参数α，β，δ和μ。

第二类概率分布族用 QII(y;α-，α+，β-，β+，μ)来表示，主要用于拟合具有极端不平稳尾部特征的数据分布，其分位数函数可以表示为：

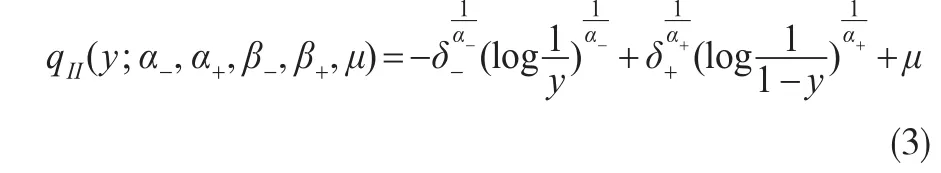
其中，模型参数 α-，α+，β-，β+∈R+，μ∈R ，并且我们主要关注的是参数α-≤1，α+≤1时的情形。与第一类分布相同，参数α-和α+也用来衡量分布左右尾部的厚度。

在上述分位数概率模型的基础上，我们可以方便的计算出金融资产收益率的分位数和对应的风险价值。设R(t)表示某项资产或资产组合在持有期T内的收益率，VaRθ表示该资产或资产组合在置信水平为1-θ（0＜θ＜1）下的风险价值，则

其中，q(y)为R(t)的样本分位数函数。

3 模型的实证分析

3.1 数据的选取及其统计特征

本文选择美国标准普尔500指数（S&P500）、香港恒生指数（HSI）、上证综合指数（SSEC）和深圳成份指数（SZSC）为样本进行研究。为保证研究时期的一致性，所有样本采用2008年1月1日到2013年6月30日的大盘日收盘价格指数进行分析，数据全部来自雅虎财经网（www.yahoo.com）。下图1给出四种股票指数在样本期内的走势特征。

图1 S&P500、HSI、SSEC、SZSC的走势特征

日收益率采用连续对数收益，即 ri=lnPt-lnPt-1，其中Pt为每日收盘的指数价格。表1给出两种大盘指数的对数收益率的统计特征。从表1我们可以看出：

除标准普尔500指数外，其他三种指数的收益率均值均小于零；四种指数中，深证成分指数的波动最大，标准差为0.0201，标普500指数由于其市场成熟度较高，故波动性最小，标准差为0.016；另外，四种指数的收益率的峰度都大于3，J-B统计量较大，说明其收益率分布都具有尖峰厚尾和非正态性分布的特征。

表1 收益率统计特征

3.2 基于第一类分位数分布的VaR模型的构建

3.2.1 第一类分位数概率模型的估计结果

利用Q-Q（Quantile--Quantile）估计方法，我们得到基于第一类分位数分布拟合四类股票指数收益率的参数估计结果（见表2）。通过Q-Q图展示了S&P500、HSI、SSEC和SZSC收益率的理论分位数与实际分位数的拟合情况发现：从四个图的拟合效果来看，除了样本尾部数据的几个异常点外，理论分位数和实际分位数基本在一条直线上，这说明第一类分布的拟合效果较好。进一步分析发现，上证综合指数和深圳成分指数的收益率拟合效果要优于标普500指数和恒生指数的收益率。这可能和国内股市的涨停板制度有显著关系，涨停板制度的实施有效地限制了股票市场的大幅波动，从而使得大盘指数出现异常收益率的几率大大降低。从表2的参数估计分析，我们发现四类指数的拟合估计β值都显著大于1，这说明四类股票指数分布的左尾都比右尾更厚，呈现出左右尾部不对称的特点，这提示我们当不利消息冲击股市时，其损失将大于有利信息冲击股市所带来的收益。另外，四类股票指数分布的α都小于1，说明其收益率分布的尾部厚度大于正态分布的尾部厚度。

3.2.2 基于第一类分位数分布的VaR模型

在实证研究中为了检验第一类分位数VaR模型的准确性，我们分别采用静态和动态两种方式进行VaR的建模估计。所谓静态VaR模型就是将样本期内所有数据都用于第一类分位数模型的估计，进而计算出所有样本期的VaR风险值。另外一种情况，我们也考虑不同人可能选取不同的样本长度进行VaR估计，这些不同样本期间内得到VaR值会不会有显著的不同呢？它们之间是否会呈现某种特征呢？这促使我们考虑通过数据平移的方式来进行动态VaR估计，其建模的规则是：将样本的收益率数据分为建模样本和检验样本两个部分，采用样本期内的后500个数据用于模型检验，前面的数据用于建模，并逐次向后平移数据形成动态VaR序列。例如对于上证综指的1374个样本收益率中的前874个数据用于建模，后500个用于日VaR估计值的回顾测试，具体建模中采用数据的平移滚动方式进行估计，即用1～874个数据估计分位数模型并计算出第一个VaR值，再通过平移选取2～875个数据计算出第二个VaR值，…..，以此类推，我们可以得到一个VaR序列，其包含有500个VaR值，并用该VaR系列值与后500个日收益率数据进行比较，从而检验动态VaR模型估计风险的效果。

（1）静态模型的估计结果。

表2中四类指数收益率的估计参数分别代入（1）式，并令置信度θ=0.01，我们得到置信水平为99%的VaR估计值，其结果如表3所示：

表3 四种股票指数的静态VaR估计值

从上述结果可以看出，在整个样本期内，基于成熟市场的标普500指数和恒生指数的VaR风险值要明显小于国内的上证指数和深证成指的VaR值。同样置信水平下，深证成指的风险最大。

（2）动态模型的估计结果

如上面所述，我们采用滚动平移的方式，分别做出标普 500指数（S&P500）恒生指数（HSI）、上证综合指数（SSEC）、深证成分指数（SZSC）在置信水平99%下的VaR序列图（图略）。并在表4中给出三种股票指数收益率动态VaR序列的相应统计特征。

表4 四种指数收益率动态VaR序列的统计特征

4 回顾测试

建立VaR模型估计金融风险后，监管部门和金融机构必须进行后验测试（Backtesting），也称为回顾测试，即将VaR模型预测的市场风险数据和实际交易结果进行对比，以评价VaR的准确性和模型的有效性。本文采用Christoffersen（2003）给出的VaR回顾测试方法，下面对其作简单介绍。

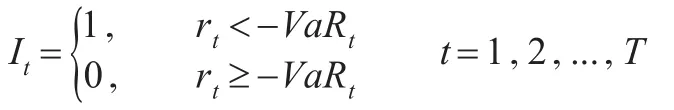
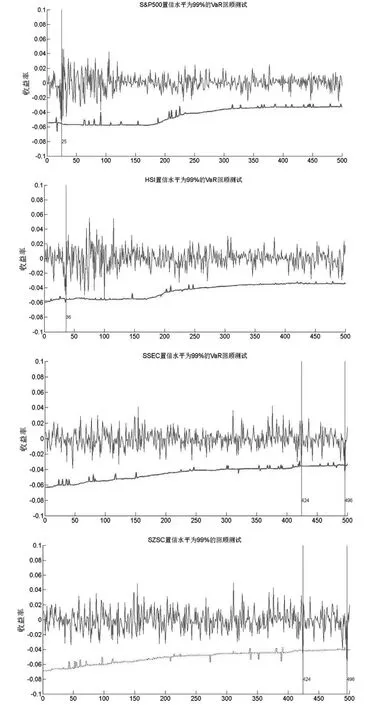
图2 四种股票指数动态VaR序列的回顾测试

从检验结果来看，S&P500和HSI各发生一次“VaR违背事件”，而SSEC和SZSC各发生两次“VaR违背事件”，都小于损失超过VaR估计值的5次理论值。由此说明，基于第一类分位数概率分布的动态VaR能够有效地度量四种证券指数的市场风险。另外，出于稳健性考虑，我们也采用Kuipec（2005）提出的LR统计量来检验VaR预测违背比率π是否显著不同于预设的显著水平 p，即H0: π=p；H1: π≠p。在零假设下LR似然比统计量服从自由度为1的卡方分布，即

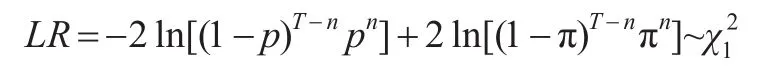
其中，T样本测试期，n为样本测试期内“VaR违背事件”的发生次数，=n T为测试失败率，p为显著性水平。若零假设成立，在99%的置信水平下的分位数为6.635，若LR＞6.635，则拒绝原假设，对应的VaR模型也被拒绝。表5显示LR似然比检验的结果。

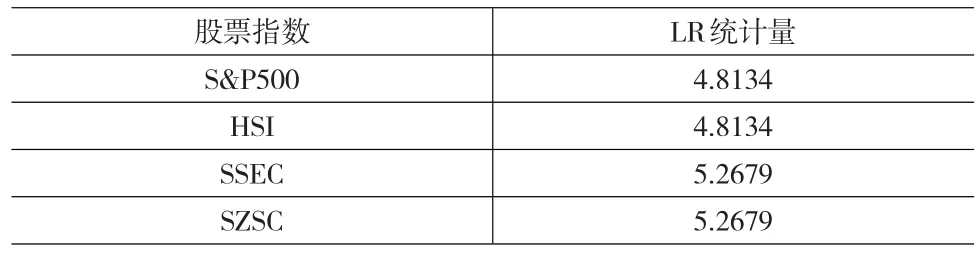
表5 LR统计量的检验结果

5 总结

本文在蒋文江教授和邓世杰教授提出的一类新型分位数概率分布的基础上，提出基于新型分位数分布的动态VaR模型，其优点在于其直接对条件分布的分位点进行建模，而不依赖于特定的分布形式和分布参数，体现由数据选择模型的思想，特别适合于厚尾分布数据的应用。通过对标准普尔500指数，香港恒生指数、上证综合指数和深证成分指数的实证检验，回顾测试显示，我们的分位数动态VaR模型能较好地度量证券市场风险，其该模型在发达证券市场的表现优于国内证券市场的表现。

[1]Press S J.A Compound Event Model for Security Prices[J].Journal of Business,1987,40(3).

[2]Mantegna R,Stanley H E.Scaling Behavior in the Dynamics of an Economics Index[J].Nature,1995,376.

[3]Verhoeven P,Mcaleer M.Fat Tails and Asymmetry in Fiinancial Volatility Models[J].Mathematics and Computers in Simulation,2004,64.

[4]潘家柱，丁美春.GP分布模型与股票收益率分析[J].北京大学学报（自然科学版），2000，（3）.

[5]卢方元.中国股市收益率分布特征实证研究[J].统计与决策，2004，（4）.