修正灰色模型在路基沉降预测中的应用

■ 薛志杰

0 引言

高铁路基沉降变形监测是高铁运营维护观测的重要内容[1]。合蚌高铁淮南东站路基观测地段位于淮南东站小里程方向，属高路堤地段。

灰色系统是指部分信息已知而部分信息未知的系统，灰色系统所要考察和研究的是对信息不完备的系统，通过已知信息来研究和预测未知领域从而达到了解整个系统的目的[2-3]。灰色模型[4]在进行趋势预测方面并不需要典型的和较长的数据列，为此将其引入淮南东站路基沉降监测中，进行沉降变形预测。

1 传统灰色预测模型简介

灰色模型是灰色理论中最常用的模型之一。它的建模是对生成数列的建模，对原始数据没有大样本的要求，只要原始数列有4个以上的数据就可以通过变换来建立模型。

灰色模型建模的思路是：将实测得到的离散的、随机的原始沉降－时间序列经过累加处理，得到规律性较强的累加生成序列；然后根据该序列建立灰色微分方程，通过对数据序列的拟合，求得灰色微分方程的参数，从而获得灰色预测微分方程；最后将灰色预测微分方程计算结果进行累减后即可得到预测值。灰色理论的微分方程型模型应用最广泛的就是G M（1，1）模型，即1阶1个变量的微分方程型模型，其建模过程如下[4]。

（1）对原始非负序列：

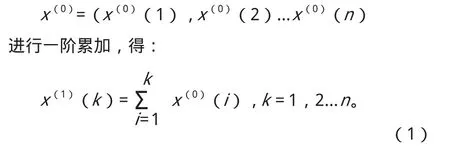
其中，一次累加序列的第k项由原序列的前k项和产生。

（2）利用此序列生成紧邻均值序列：

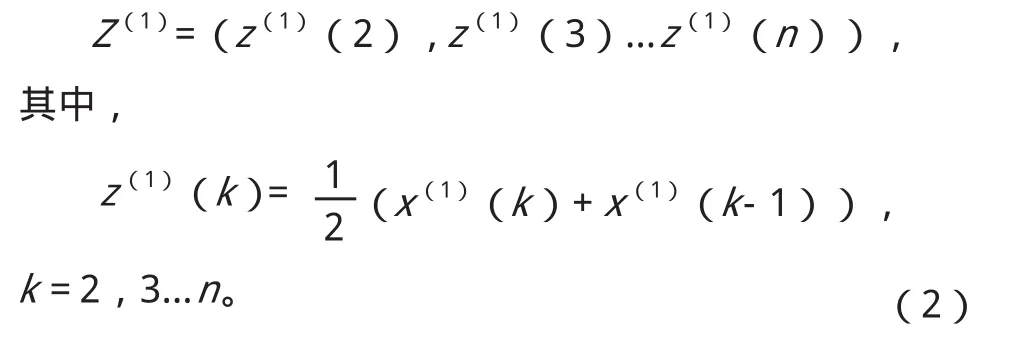
（3）建立灰色GM（1，1）模型的一级白化微分方程：

（4）构造G M（1，1）模型方程组的矩阵形式。令A=（a，b）T为参数列，且：

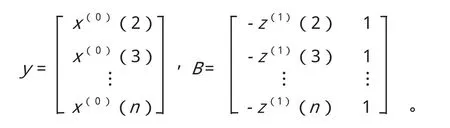
方程组的矩阵形式为：Y = B A。

按照最小二乘法估计参数列A=（a，b）T，得：

将计算求得的参数a、b带入式（3）求微分方程，取x(1)（1）= x(0)（1），可得到灰色G M（1，1）预测模型为：

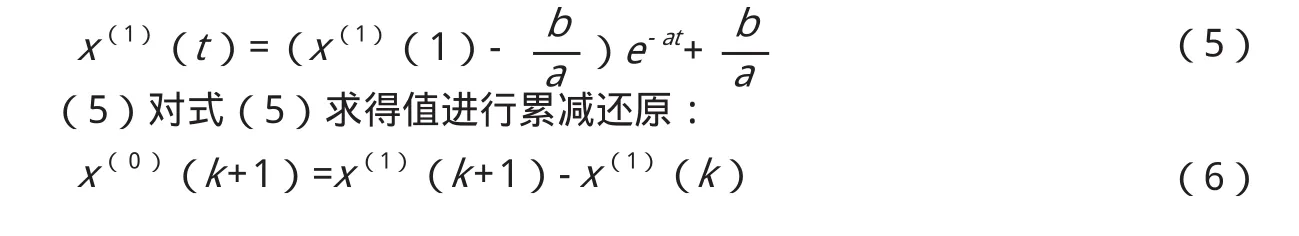
2 修正灰色预测模型简介

上述灰色预测模型是建立在观测时间基本相等（等时距）基础之上的，但由于施工、天气等因素影响，获得的沉降数据往往不是等时距的，这就要求对预测模型进行适当的修正[5]。

当沉降数据为非等时距时，对矩阵B 作相应处理。

设：

其中，△tj= tj+1- tj，j = 1，2…n - 1。B＊= T·B，用B＊代替原来的B得：

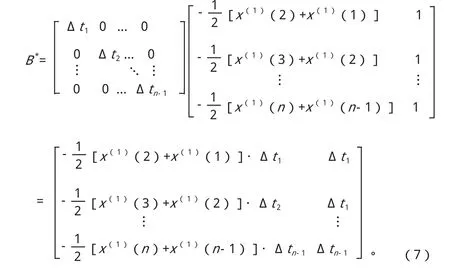
把B＊带入式（4）中就可以得到修正后的参数a、b。

3 灰度预测应用

3.1 工程概况

根据T B 1 0 6 0 1—2 0 0 9《高速铁路工程测量规范》路基地段在沉降较大区按照每块轨道板布设1个断面，在此区域外大小里程按照1 0、2 0、4 0 m布设断面。每个断面设置8～9个监测点：两侧路肩各1个、上下行线支承层各1个、上下行线左侧轨顶各1个、上下行线轨道板中各1个，另外线路间沉降板一并纳入监测断面。

以合蚌高铁淮南东站K 8 8 9+6 7 2重点路基地段断面3 0 3 9 2 3 C PⅢ点沉降实测数据进行灰度预测。该断面共监测7期，获得6次沉降量数据（见表1）。

表1 K889+672断面各期沉降量数据观测时间 沉降量/时间 备注mm序列2 0 1 3-0 5 5.1 1 2 0 1 3-0 6 2.5 1 2 0 1 3-0 7 1.3 1 2 0 1 3-0 8 1.8 1.6 相隔时间较长2 0 1 3-0 9 0.5 1 2 0 1 3-1 0 0.4 1 验证用

3.2 模型预测

首先，把表1中的沉降量数据通过式（1）、（2）依次进行变换，把变换结果带入式（4），求得参数a、b。通过式（1）、（2）、（7）依次进行变换，把变换结果带入式（4），求得修正参数a、b。

其次，将上述2种参数带入式（5），求得传统灰色预测模型和修正灰色预测模型（见表2）。

再次，将传统时间序列和修正时间序列数据带入2种预测模型，通过式（6）求得原始数据预测值（见表3）。

表2 2种预测模型计算公式及精度评估模型 传统模型 修正模型预测公式 -8.0 7 2 7e- 0.3 5 1 8 t + 1 3.1 7 2 7 -6.8 1 5 6e- 0.4 2 3 4t + 1 1.9 1 5 6均方差比值C 0.1 0 9 0.0 9 0小误差概率P/％ 1 0 0 1 0 0表3 原始数据与2种预测模型数据预测值观测时间 原始数据/mm 传统模型预测值/mm 修正模型预测值/mm 2 0 1 3-0 5 5.1 5.1 0 0 5.1 0 0 2 0 1 3-0 6 2.5 2.3 9 4 2.3 5 3 2 0 1 3-0 7 1.3 1.6 8 4 1.5 4 1 2 0 1 3-0 8 1.8 2.0 1 8 1.6 6 9 2 0 1 3-0 9 0.5 0.5 8 6 0.4 3 3 2 0 1 3-1 0 0.7 0 2 0.4 6 9 2 0 1 3-1 1 0.2 0 4 0.1 2 1

最后，将表1中的沉降量原始数据和拟合值带入式（8）、（9），即可求得C和P（见表2）。

通过以上数据分析可知，修改预估模型预估2 0 1 3年1 0月沉降量为0.4 6 9 mm，通过现场测量数据为0.4 mm，相符程度远高于传统模型预测值。

4 结束语

（1）修正预测模型突破了传统预测模型等间隔时序系统的限制，拓宽了模型在实际预测中的适用范围。

（2）采用传统预测模型和修正预测模型预测合蚌高铁淮南东站K 8 8 9+6 7 2断面处运营期的沉降量，结果表明经过修正的预测模型预测值精度更高，更符合工程实际运用。

（3）高速铁路运营期路基段沉降监测分析需综合考虑观测的时间不是等间隔的，通过使用合理的预测模型可以及时进行准确预测，为后续的观测频次调整及整治提供准确依据。

[1] T B 1 0 6 0 1—2 0 0 9 高速铁路工程测量规范[S].北京：中国铁道出版社，2 0 0 9.

[2] 兰孝奇，严红萍，刘精攀. 灰色系统预测模型在沉降监测中的应用[J]. 现代测绘，2 0 0 6，2 9(1)：2 4-2 6.

[3] 刘思峰. 灰色系统理论的产生与发展[J]. 南京航空航天大学学报，2 0 0 4，3 6(2)：2 6 7-2 7 2.

[4] 邓聚龙. 灰理论基础[M]. 武汉：华中科技大出版社，2 0 0 2：2 0 8-2 3 9.

[5] 杜彦良，姬来，刘新福. 高速铁路路基施工沉降量的灰色预测模型及应用[J]. 铁科学与工程学报，2 0 0 9，6(1)：3 6-4 0.