加入信道估计误差的MIMO双向中继最大和速率的研究*
卢雅哲,陈 宇,刘 璐,束 锋,2*
(1.南京理工大学电子工程与光电技术学院,南京210094;2.东南大学移动通信国家重点实验室,南京210096)
因为无线中继传输系统可以拓宽覆盖范围和提高系统容量,所以是一个有前景的研究课题。文献[1-3]都是研究分析中继系统容量的文章。为了提高中继网络的容量,我们需要考虑点对点多天线输入多天线输出(MIMO)的情况[4]。MIMO中继系统的容量在文献[5]中有研究。大部分中继系统都是假设工作在半双工情况下的,也就是中继不同时接受和发送信息,这样可以避免中继节点的环路干扰。
文献[6-7]中通过研究双向中继协议来克服半双工频谱效率损失。在第一个时隙,两个源节点同时发送信息给中继;在第二个时隙,中继节点传输先前的信号给用户终端。因为每个终端节点都知道其自身的信道状态信息,所以在终端节点可以消除自身的干扰[7]。相比于需要四个时隙传输信号的单向中继协议来说,双向中继协议只需要两个时隙。所以,双向中继协议可以从半双工中继信号中补偿一大部分的容量损耗。因此双向中继是目前研究的热点。
在实际中继系统中,因为放大转发AF(Amplify and Forward)方式中继节点只需要线性处理基带信号,不需要解码信号,所以它相比于解码转发方式易于实现而且有着较低的计算复杂度。文献[8]研究了一个基于奇异值分解SVD(Singular Value Decomposition)的线性方法去实现MIMO AF单向中继系统的系统容量。对于双向中继而言,迫零ZF(Zero Forcing)和最小均方误差 MMSE(Minimum Mean Square Error)算法在文献[9]中都有所研究。文献[10]研究用户单天线中继多天线的AF双向中继系统,文中利用迭代算法计算基于最大和速率的权值矩阵。文献[11]研究用户和中继都是多天线的MIMO AF双向中继系统,文中利用梯度下降法迭代运算得出最优权值矩阵F。
本文在文献[11]的基础上引入了信道估计误差,在非理想的状态下推导出更一般的最优权值矩阵F的计算公式,这是本文的一大创新点。计算系统和速率和相应的误码性能,对比不同估计误差下的通信性能,结合通信系统对性能的要求得出我们在进行信道估计中需要满足的精度。
在本文中(·)T、(·)H分布表示矩阵的转置和共轭转置,(·)*表示矩阵的共轭。ε表示期望,IN表示N×N的单位矩阵,tr(A)表示矩阵的迹,|A|表示矩阵的行列式。
1 系统基本模型
假定MIMO双向中继系统中用户有M根天线中继有N根天线如图1所示。两个用户通过一个中继相互通信,并且工作在时分双工模式。本文我们假设两个用户节点可以直接通信忽略大尺度衰落。
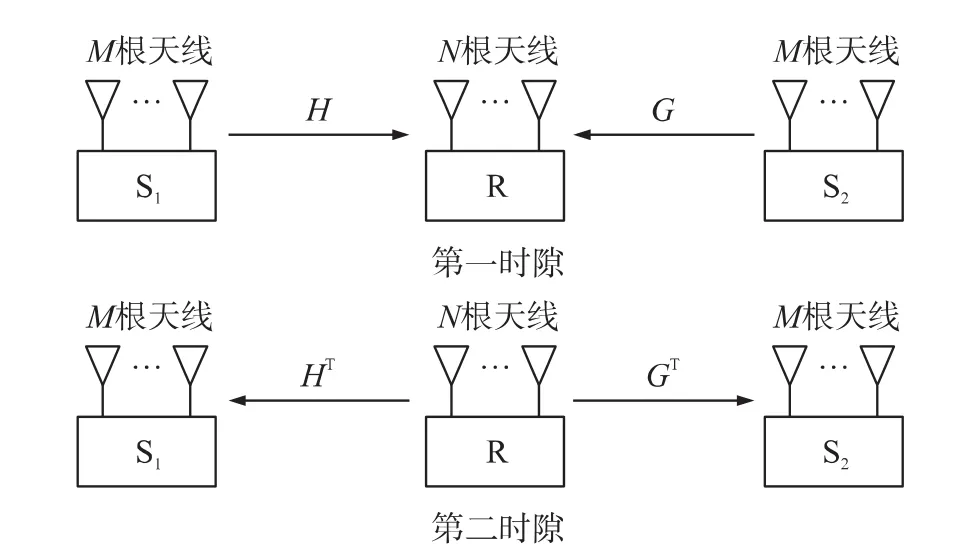
图1 系统信道模型
我们需要为信道估计误差建模,在本文中,我们引入文献[12]定义的Gauss-Markov模型。

其中H是真实信道,H^是估计信道,噪声E服从零均值单位方差高斯随机分布。标量β表征了节点对信道信息的了解情况。当β=0时,意味着知道完美的CSI,估计信道等于实际信道,当β=1时意味着完全不知道信道信息。这是两种极端的情况,实际的信道估计在这两种情况之间。
在第一个时隙,两个终端节点同时把它们的信号sA和sB传送给中继节点R。然后接收到的N维信号向量r为:

其中H和G是从终端S1和S2到中继端的N×M维信道矩阵,n是零均值复高斯随机噪声ε(nn+)=IN,sA和sB是M维传输信号向量其中PA和PB是终端S1和S2的功率。
在第二个时隙,中继端进行线性处理乘以权值矩阵F。那么中继节点要传输的信号向量x为:

其中 γ是功率规格化系数,满足功率约束条件ε{tr(xx+)}=PR,可以表示为:

中继端处理过后的信号x从中继节点传输到终端节点S1、S2,如图1所示,广播信道矩阵为HT和GT,所以在两个终端节点接收到的信号yA和yB可以表示为:
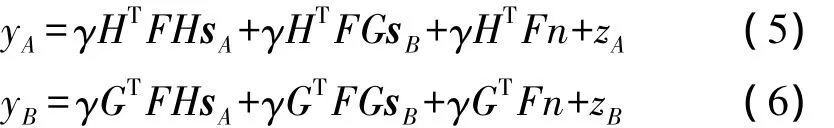
其中zA和zB是协方差矩阵为IM的复高斯白噪声。
因为在终端节点我们知道所估计的信道,但是由于信道存在估计误差,所以自干扰不可以完全消掉。自干扰项减去估计的信道,我们可以得到最终终端节点和为:
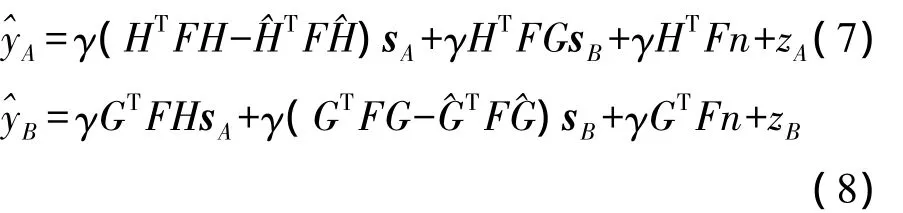
从式中我们可以得出双向中继的性能取决于权值矩阵F。下面一节我们将要计算一个满足和速率最大化的权值矩阵F。
2 最大化和速率
假设在式(7)、式(8)信号的总噪声是零均值圆周对称的复高斯分布,则MIMO双向中继系统的和速率可以表示为:
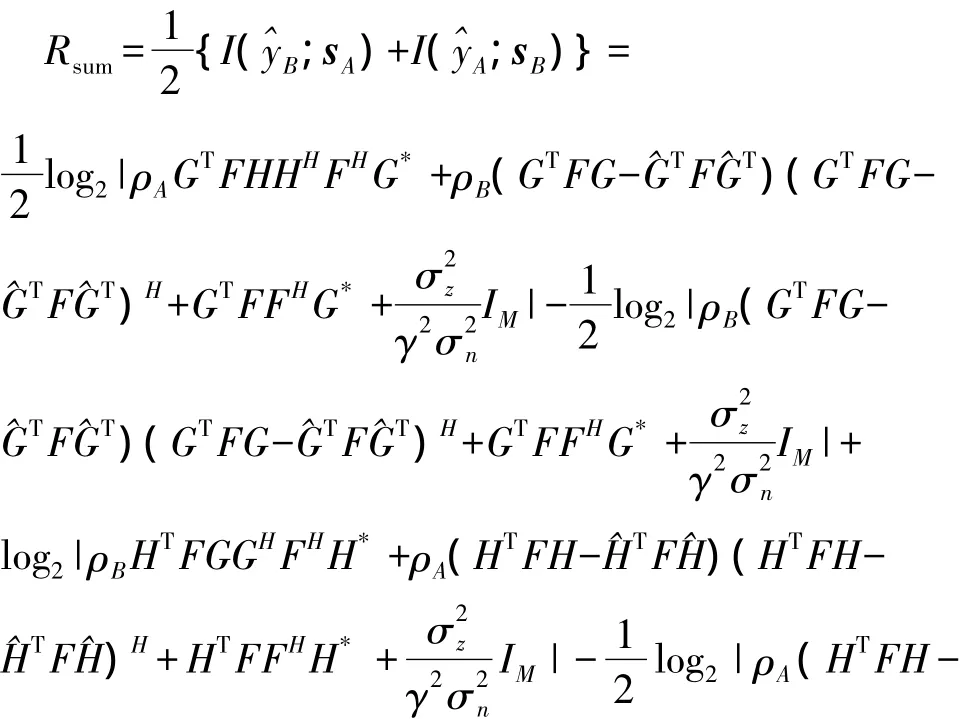
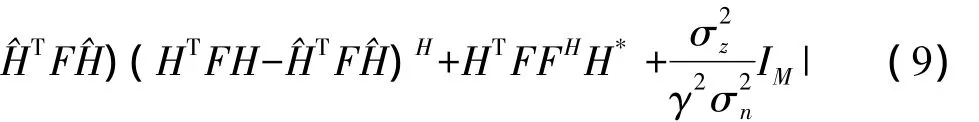
其中I(x;y)表示x和y的互信息量,因为它们工作在半双工的模式下,所以要乘以系数1/2,γ是由式(4)给出的值。
接下来,为了找到使得和速率最大的最优中继权值矩阵F,我们把问题描述成为:

因为函数Rsum不是关于F的一般凸函数或凹函数,所以它的最大化问题难以分析和解决。在本文中我们引入文献[11]所提出的梯度下降算法来解决式(10)最优化问题。
因为和速率Rsum是一个实函数,所以我们可以认为为了计算简便,我们设:
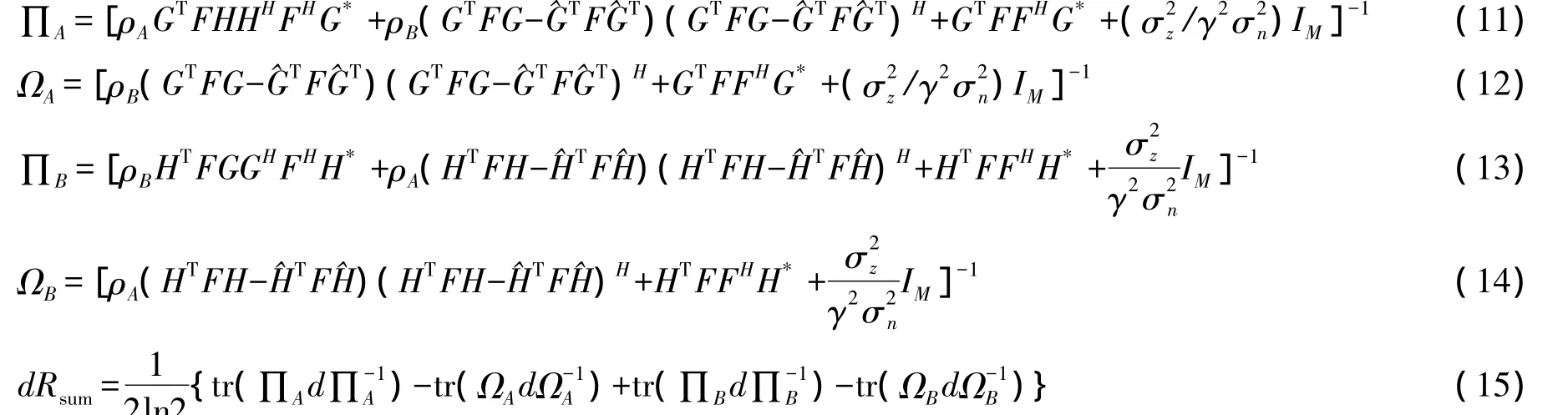
速率和的微分式(9)可以写为式(15)。在这里我们考虑了 γ也是 F的函数。这个结果可以用公式[∂tr(AXX+B)]/∂X+=BAX来证明。那么和速率的梯度可以表示成为:

得出梯度公式,我们运用迭代算法解决式(16)问题

在这个迭代过程中,ε是终止容忍值。文献[13]中给出了一些确定步长的线性搜索方法。我们采用Armijio’s Rule方法搜索步长,则步长δ可以表示为δ=vm,其中m是满足下面式子的最小整数

在这里v和μ是0到1范围内的一个确定的值。
因为该问题是一个非凸问题,所以迭代算法并不能保证全局最优,所以我们为了保证得到的矩阵最优,就要产生多个初始值多次迭代,然后从所得的结果中选出最优值。
3 仿真结果
在这个部分我们要仿真不同信道误差估计下的最大和速率和误码性能。在仿真中我们设PA=PB=P/4,,其中P是中继网络的功率。SNR=P/,其中H和G的元素是独立同分布的零均值单位方差复高斯信道。我们在仿真中初始化F权值矩阵10次以得到全局最优。
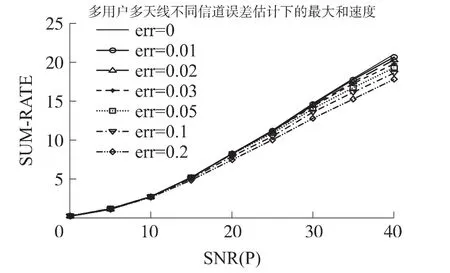
图2 不同估计误差下的最大和速率
在图2中,我们选择β的取值分别为0、0.01、0.02、0.03、0.05、0.1、0.2;选择用户天线个数M=2,中继天线个数N=4,噪声的方差==1,为了使得到的最优值为全局最优,我们设置20个初始值来计算并从中选择最优值。从图2中可以得出,随着信道估计误差的增大最大和速率均匀下降,所以我们要保证一定的信道估计误差来保障和速率。
在图3中,我们选择β的取值分别为0、0.01、0.02、0.05、0.1;天线数目和噪声与上面相同,从图3中可以得出,随着信道估计误差的增大误码性能随之下降,尤其在高信噪比的情况下下降更多,我们可以看出,当信道估计误差超过0.05的时候系统的误码性能就会变得非常差,所以我们要保证一定的信道估计误差不能超过这一值。

图3 不同信道估计
4 总结
在这篇文章里,我们研究了加入信道估计误差的最大和速率问题。我们运用了梯度迭代法计算波束成形矩阵F,对比了不同信道估计误差下的最大和速率和误码性能,得出在该算法下为了保证通信质量必须控制信道估计的误差不能太大。由于现实中,信道估计不可能完全没有误差,所以这个研究具有很强的现实意义,也是目前国内外学者的一个研究热点。
[1]Cover T M,El Gamal A A.Capacity Theorems for the Relay Channels[J].IEEE Trans Inform,1979,25(5):572-584.
[2]Gastpar M,Vetterli M.On the Capacity of Wireless Networks:The Relay Case[J].Proc IEEE Infocom,2002(3):1577-1586.
[3]Kramer G,Gastpar M,Guptar P.Capacity Theorems for Wireless Relay Channels[J].Allerton Conf Comm,Control and Comput,2003:1074-1083.
[4]Wang B,Zhang J,Host-Madsen A.On the Capacity of MIMO Relay Channels[J].IEEE Trans Inform Theory,2005,51(1):29-43.
[5]Bolcskei H,Nabar R U,Oyman O,et al.Capacity Scaling Laws in MIMO Relay Networks[J].IEEE Trans Wireless Comm,2006,5(6):1433-1444.
[6]Rankov B,Wittneben A.Spectral Efficient Signaling for Half-Duplex Relay Channels[C]//Proc IEEE Asilomar Conf on Signals,Systems and Comput,2005.
[7]Rankov B,Wittneben A.Spectral Efficient Protocols for Half-Duplex Fading Relay Channels[J].IEEE J Select Areas Comm,2007,25(2):379-389.
[8]Tang X,Hua Y.Optimal Design of Non-Regenerative MIMO Wireless Relays[J].IEEE Trans Wireless Comm,2007,6(4):1398-1407.
[9]Unger T,Klein A.On the Performance of Two-Way Relaying with Multiple-Antenna Relay Stations[J].IST Mobile and Wireless Comm Summit Budapest,2007.
[10]Namyoon Lee,Hyun Jong Yang.Achievable Sum-Rate Maximizing AF Relay Beamforming Scheme in Two-Way Relay Channels[C]//ICC Workshops’08.IEEE,Beijing,2008.19-23.
[11]Lee Kyoung-Jae,Lee Kwang Won,Sung Hakjea.Sum-Rate Maximization for Two-Way MIMO Amplify and Forward Relaying Systems[C]//Vehicular Technology Conference,IEEE 69th,Barcelona,26-29 April 2009.
[12]Wang C,Au E K S,Murch R D,et al.On the Performance of the MIMO Zero-Forcing Receiverin the Presence ofChannel Estimation Error[J].IEEE Trans Wireless Commun,2007,6(3):805-810.
[13]Bazaraa M S,Sherali H D,Shetty C M.Nonlinear Programming:Theory and Algorithms[M].3rd Ed.New York:John Wiley and Sons,2006.

