假设判定是列表法解决“鸡兔同笼”问题的捷径

鸡兔同笼是北师大版五年级上册第80～81页的内容，解决鸡兔同笼的方法很多，教材选“鸡兔同笼”这个题材，主要不是为了解决“鸡兔同笼”问题本身，而是要借助“鸡兔同笼”这个载体让学生经历列表、尝试和不断调整的过程，从中体会出解决问题的一般策略——列表。在后面相应的练习中，相关的题目也都附上了表格，能够让学生较好地运用这种基本的解题策略。

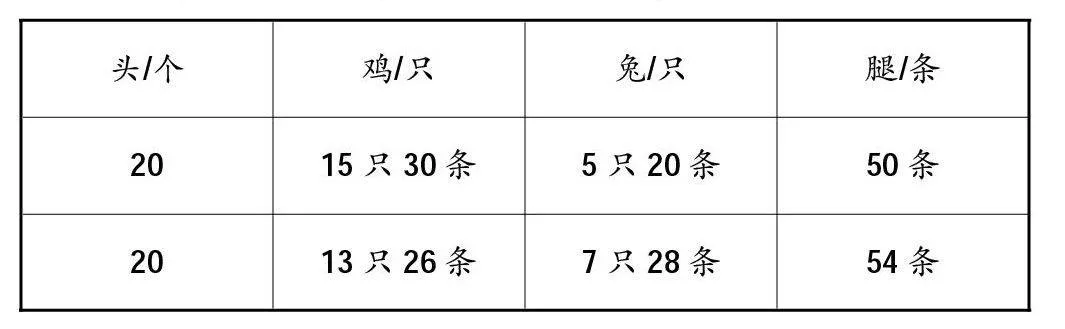
鸡兔同笼，有20个头，54条腿，鸡、兔各有几只？教材呈现了三种列表举例的方法。其中第一张表格是常规的逐一举例法，根据鸡与兔共20只的条件，假设鸡只有1只，那么兔就有19只，腿共有78条，从1只鸡开始一只一只地试。……经过了13次计算得到正确答案。第二张表格采用跳跃列举法。先从鸡只有1只，兔就有19只，腿共有78条尝试，再作一些分析，这么多腿，兔子太多了，第二次就改成5只鸡，15只兔来试，后面每次增加5只鸡，或者每次增加不同数量的鸡的只数，跳跃列举，以减小举例的次数。第三张表格是采用取中列举法。由于鸡与兔共20只，所以各取10只，接着在举例中根据实际的数据情况确定举例的方向，这样可以大大缩小举例的范围。

在实际教学中，以上三种方法，在我们成人看来看似简单，但由于每道题都要经过多次尝试列举，才能找到答案，不少孩子在解决问题时总是错误不断，思考方法也无序，列表怎么也列不清楚。怎样才能减少列举的次数，让孩子有序地思考呢？有一天，我突发灵感，何不把假设法和列表法结合在一起，先假设全部是鸡和兔分别求出腿数，谁接近已知腿数，谁的只数就多一些，再列表，岂不更简洁。经过多次尝试，如采用我的假设判定法后再列表，一般列举2～3次就能解决问题，很容易被学生掌握。下面以教材中的例子为例加以说明。

假设判定：

20×2=40（条）（假设全部是鸡）

20×4=80（条）（假设全部是兔）

54接近40一些，鸡多一些。列表时假设鸡取15只，兔5只，共50条腿，还少4条腿，说明兔子少2只，调整鸡减2只。

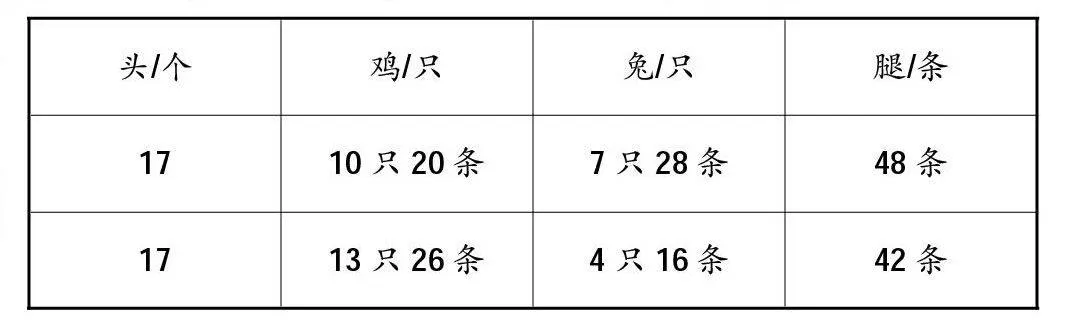
再举例：鸡兔同笼，有17个头，42条腿，鸡兔各有几只？

假设判定：

17×2=34（条）（假设全部是鸡）

17×4=68（条）（假设全部是兔）

42接近34一些，鸡多一些。列表时假设鸡取10只，兔5只，共48条腿，多了6条腿，说明兔子多3只，调整鸡加3只。

自从采用了我的假设判定再列表的方法后，学生很少出差错。

（作者单位 浙江省义乌市开发区宏迪路65号）