让图形直观成为学生思维的源泉

摘 要：直观是一种重要的教学手段。在小学数学教学中，合理利用图形直观，既充分体现出了数形结合的数学思想，也体现出数学学科的重要性质。利用图形直观，给学生一个思维的支点，能帮助学生的思维切入基本点、捕捉生长点、构造交接点、把握中心点。

关键词：图形直观；基本点；生长点；交接点；中心点

直观是一种重要的教学手段。在实际的小学数学教学中，合理利用图形直观，可以帮助学生找到思维的支点，能够更好地促进学生理解、掌握、建构知识，发展学生的思维。那么，在实际的教学中如何利用图形直观，让它成为一个有效的载体，真正成为学生思维的源泉呢？下面结合自己的教学实例，谈谈自己的一些做法和体会。

一、图形直观，切入基本点

利用图形直观，抓住概念的本质，以知识本身为基本点，可以帮助学生修正自己的猜测，感悟“做数学”，提升思维品质。如，教学四年级下册的“三角形三边关系”，有许多的教学案例出现，学生认为两边之和等于第三边的情况是能够做成三角形的。我通过观察、分析，发现问题就出在缺乏概念支撑上。当学生用小棒做三角形时，课堂上我就让学生反馈一下，做的三角形在哪里，让学生指一指边、角、顶点。用的材料是“围”成三角形，而不是拼搭，必须有三个角、三个顶点、三条边，缺其中之一都无法围成三角形。图形直观，概念抽象化出边、角，实现对三角形三边关系的真正意义的理解，让学生的判断力有所依靠，在否定自己的认识和推理过程中来建立、优化对数学知识的正确认识。利用图形直观，帮助学生切入到思维的基本点，培养学生探究意识的同时发展思维的正确性和深刻性。

二、图形直观，捕捉生长点

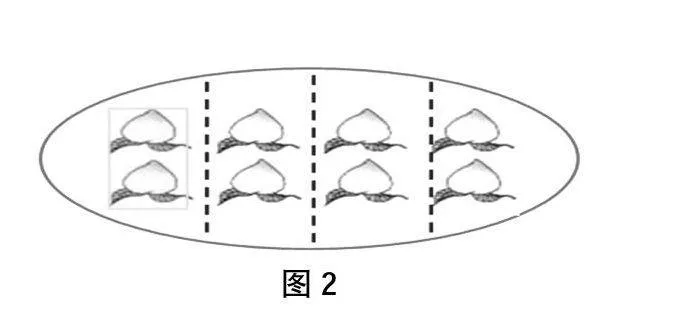
利用图形直观，发挥其符号意义的功能，以旧知识为生长点，能更好地促进学生对新知识的接纳和理解，实现“同化”与“顺应”。如，教学三年级下册“分数，认识几分之一”时，学生对把由许多个物体组成的整体来平均分，总会受个数的影响，难以理解把一个整体平均分成几份，每份是这个整体的几分之一。我看过的课例中都重新创新教材，回避把4个物体（桃）平均分的情况，直接出现8个物体平均分，仍会出现平均分成4份，每份是整体的八分之二。应对课堂，回避总不是问题。再回到4个桃平均分，如图1，学生很容易理解每份是1个，这1个是这个整体（4个桃）的四分之一，分母4表示的是平均分成4份，分子1表示的是1个1份，这1份是这个整体（4个桃）的四分之一。那8个桃平均分成4份，每份是这个整体的四分之一还是八分之二呢？关键还在于理解分数的意义。当学生出现理解为八分之二时，就反问学生从8等份中取2份，怎样画图？像图2的分法中还缺少什么？学生容易想到还要把这个整体（8个桃）平均分，要分成8份，还要画一条虚线，再取2份。利用图形直观，通过图式对比，变化虚线符号，让学生思维的由静态发展到动态，直观中精细化，帮助学生捕捉到思维的生长点，实现了新旧知识之间的迁移。

三、图形直观，构造交接点

利用图形直观，突出其新旧知识的联系，交织融会为交接点，能够更好地促进学生对数学学习的系统认识，思维方式、方法得以提升。如教学四年级下册“倍数和因数的知识”，教材呈现出对12个小正方形拼成的长方形（教材70页图）：其意义是从三种拼法中来揭示“倍数和因数”的知识。究竟基于的起点和路径是什么呢？我想还是反馈课堂来寻求吧。课堂上学生反馈出的拼法中就有把每一种情况都竖起来的得到的是六种拼法，及是学生一图两用了。我没有否定学生的想法，而是告诉学生拼成的长4，宽3的长方形，既可以看成12里面有3个4，也可以看成12里面有4个3。正是因为学生会一图两用，顺理成章就可以揭示出倍数的概念，更好地理解为什么12是4的倍数，也是3的倍数了。当然学生再理解研究倍数和因数时为什么不研究0呢，而是研究0以外的自然数才有意义，这也就成顺其自然的事了。利用图形直观，搭建起新旧知识的联系，为学生构造出思维的交接点，获取到新知识信息的途径，让学生的思维得到顺应，强化所学知识的系统性。

四、图形直观，把握中心点

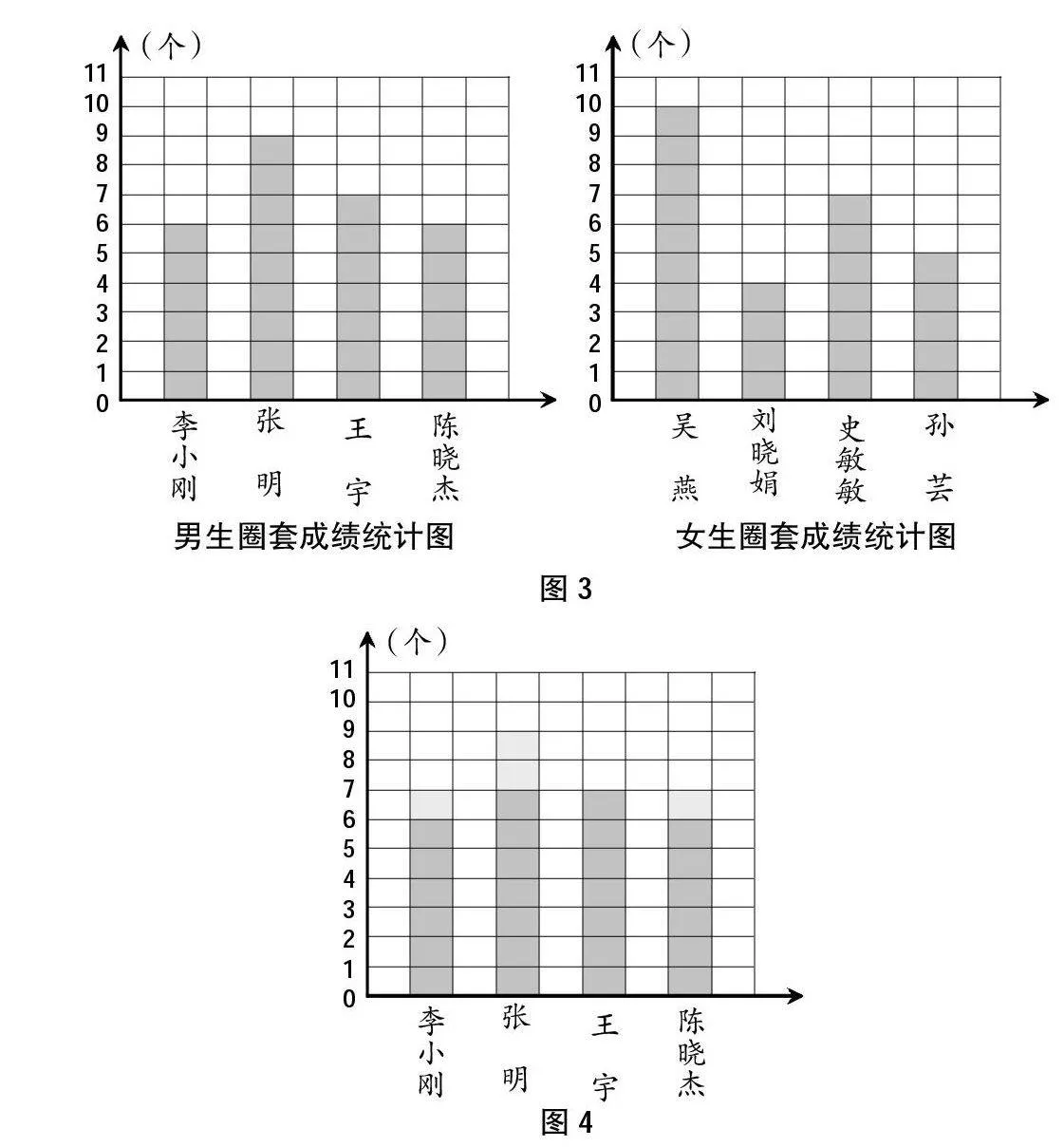
利用图形直观，强化数学知识学习的理解，以数学思维方法为中心点，培养了学生解决问题的意识。如教学三年级下册统计单元的“平均数”，处理这一部分内容时应该是一个整体性的把握，教学中应该把理解平均数的意义和求平均数的方法联系在一起，有效地整合。结合教材呈现的条形统计图，如图3，课堂上组织学生讨论男生和女生，哪一组套得准一些，究竟选取哪个数据来比较呢？学生会发现比总数、个别数据都不行，而要比整体的一般水平，即需要找到能够表示这一组数据集中趋势的一个统计量，这个统计量就是平均数。怎样求平均数呢？学生就可以借助图形直观，发现“移多补少”，这个就是求平均数的基本方法。课堂上教师及时追问学生从计算的角度来研究，怎样算呢？学生会联系学过的平均分的知识，先求和再平均分，进而得到求平均数的一般方法。再进一步追问学生平均数会不会超过最大的9个呢？如图4，为什么？学生会从移多补少的过程中，解释把最多的要移掉是减少，所以平均数不会比最大的9个大。同样，会比最小的6个少吗？为什么？学生会解释最少的是从多的那里得到的，不会比自己更少的了。变与不变，学生能够自主获得解释和理解平均数是介于最大值、最小值之间，主动形成“区间套”的数学思想。利用图形直观，知识承载思想与方法，帮助学生把握住了思维的中心点，使得学生能够“知其然，又知其所以然”，培养了学生解决问题的意识。

综上所述，图形直观是数形结合思想的重要体现，也是数学学科性质的重要体现。在实际的小学数学教学中，利用图形直观，给予学生一个思维的支点，能够帮助学生理解、掌握、建构知识，发展数学思考，促进学生的思维发展。给予儿童思维的源泉，这是苏霍姆林斯基提倡的发展儿童智力的建议。那么，在我们的数学课堂中，图形直观就是学生思维的重要源泉。

参考文献：

[1]中华人民共和国人民教育编辑部.教学大道：写给小学数学教师[M].北京：高等教育出版社，2010（04）.

[2]郑毓信.数学思维与小学数学[M].南京：江苏教育出版社，2008（08）.

[3][苏]B.A.苏霍姆林斯基.给教师的一百条建议.杜殿坤，译.北京：教育科学出版社，2010（02）.

（作者单位 江苏省张家港市合兴小学）