基于微分几何的永磁直线同步电机非线性控制方法研究*

刘 剑，崔柳月，龚志恒，刘美菊，高恩阳

(沈阳建筑大学信息与控制工程学院，沈阳110168)

永磁直线同步电机PMLSM(Permanent Magnet Linear Synchronous Motor)［1］具有机械结构简单、低摩擦阻力、无污染、无反冲、长距离高速高精度定位等优势，在很多领域发挥着重要作用。近几年来，将其应用于垂直升降系统引起了人们极大的关注。它作为电梯的曳引驱动系统，具有运行能耗低、传动效率高和占用空间小等优点，其工作状况直接影响着电梯的运行状态。然而，由于它的高精度运动会受到负载扰动、推力波动(齿槽力波动、磁阻力波动、端部效应等)的影响，因此对其控制器的设计提出更高的要求。

为了能够克服伺服系统所具有的非线性和不确定性，很多研究人员将滑模变结构控制算法［2］应用于PMLSM系统中，滑模变结构控制算法［3］具有响应速度快，稳定易实现等优点。文献［4］提出了二阶滑模控制方法，设计速度电流控制器，在出现参数和推力变化时，分别选取速度和直轴电流控制的滑模量，使系统具有良好的速度跟踪性能，并提高了鲁棒性。文献［5］提出了神经滑模控制方法，通过控制器实现位置跟踪，在线调整参数，实现了伺服系统的跟踪精度和低速平稳性。文献［6］提出自适应模糊滑模变结构控制算法，采用自适律和模糊逼近理论来逼近滑模控制器的输出，还应用自适应的切换控制器对滑模控制器的输出进行补偿。提高了系统在高加速度运动条件下的控制精度。但上述控制方法只能保证系统状态收敛到以滑模面为中心的边界层内，只能任意接近滑模，不能收敛滑模［7-8］，因此在一定程度上系统的精度得不到保证。

为此，本文采用了基于微分几何的最优控制理论(简称微分几何方法)［9-10］，它是一种没有使用任何近似线性化的方法，即可将非线性系统转化为线性系统，并完整地保留了系统的非线性特性，利用这一特点，设计一个针对线性系统的控制器完成对永磁直线同步电动机的最优控制。

1 永磁直线同步电机系统

PMLSM是一个非线性强耦合多变量的动态系统，PMLSM在d-q轴的动态数学模型可描述为:

式中ud、uq，id、iq，Ld、Lq分别为d、q轴动子电压、电流、电感;ψf为定子永磁体磁链;τ为定子极距;Rs为动子电阻;v为定子线速度;FΣ为包括负载阻力、端部效应阻力和摩擦力在内的总扰动力;M为动子和负载的总质量;Bv为粘滞摩擦系数;p为极对数。

设状态变量为x=［x1x2x3］T=［idiqv］T，输入为u=［u1u2］T=［uduq］T，输出为y1=h1(x)=x1=id，y2=h2(x)=x3=v，则PMLSM系统的数学模型可表示为

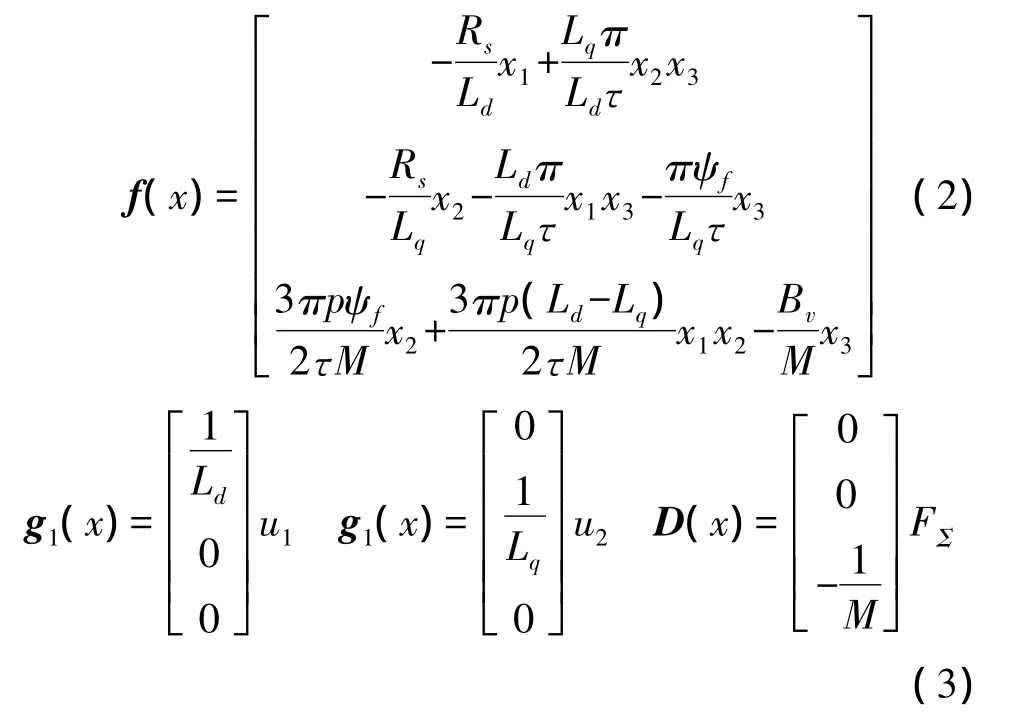
通过微分几何状态反馈精确线性化的方法把其转换成一个线性系统，再对其进行最优控制器的设计。

2 基于微分几何的状态反馈精确线性化

2.1 精确反馈线性化条件

定理1对于多输入多输出的仿射非线性系统，其表达式为:

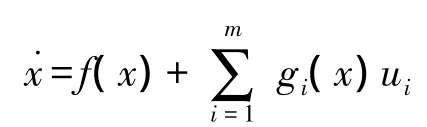
(1)n个向量场所组成的矩阵为:

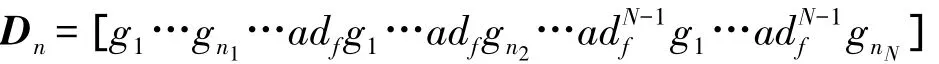
其中x0点是非奇异的;

(2)n个向量场集合中的每一个集合都是对合的。

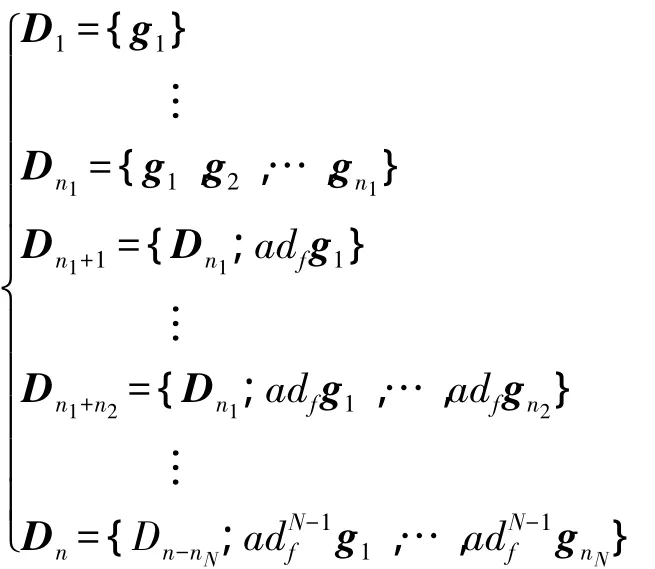
系统的输入个数m=2，故选n1=m=2，这时只能选n2=1才能使n1+n2等于状态变量的维数，从而知道N=2，nN=n2=1。根据定理1，组成3个向量场的集合为:

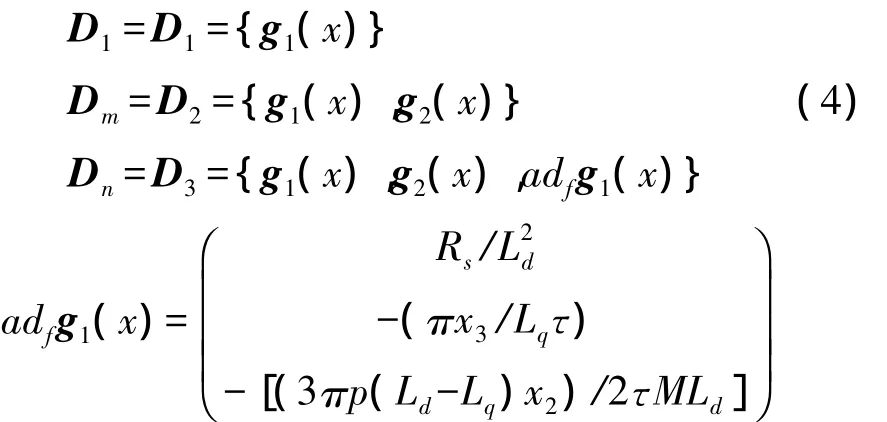
D1、D2、D3都是对合的，所以该系统可以精确反馈线性化。

2.2 精确反馈线性化原理

基于微分几何方法的精确反馈线性化是一种未使用任何近似线性化的方法，完整的保留了PMLSM系统的非线性特性，图1为其状态反馈精确线性化设计原理图。

图1 状态反馈精确线性化设计原理图

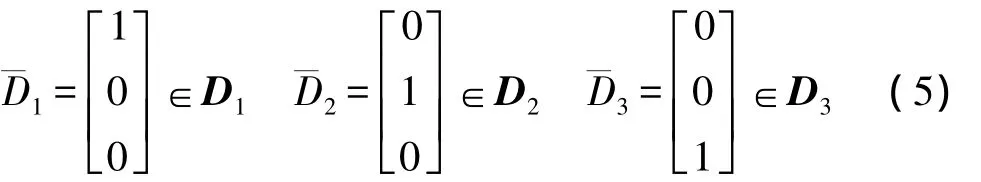
由积分曲线的概念及符号，求以新的坐标w表示的状态空间Rn到原来以x为坐标的状态空间Rn的映射x=F(w)，则:

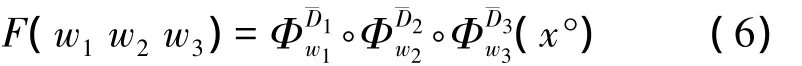
由此，解出定义的映射为:

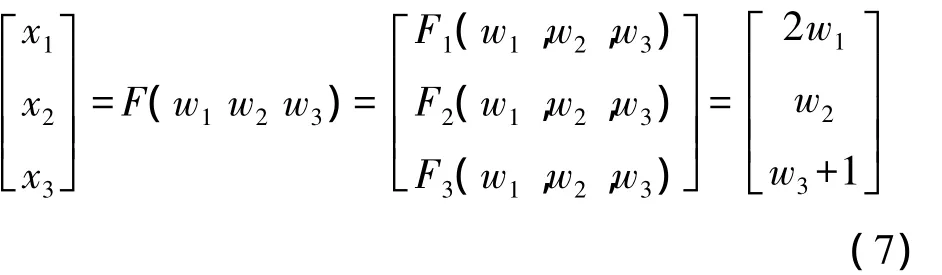
求出导出映射(f)，从而求得f(0)(w)，得到以下表达:

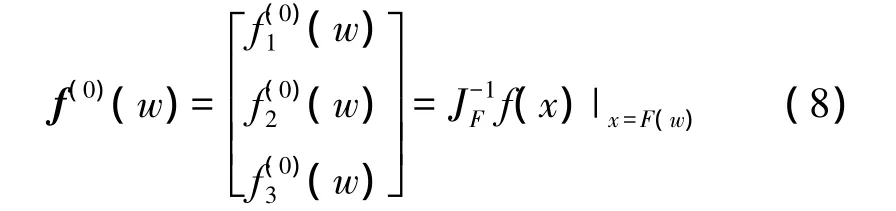
由于永磁同步直线电机系统中n1=2，n2=1，N=2，故只需求变换RN-1=R1。再相应的变换T=R1F-1应为:

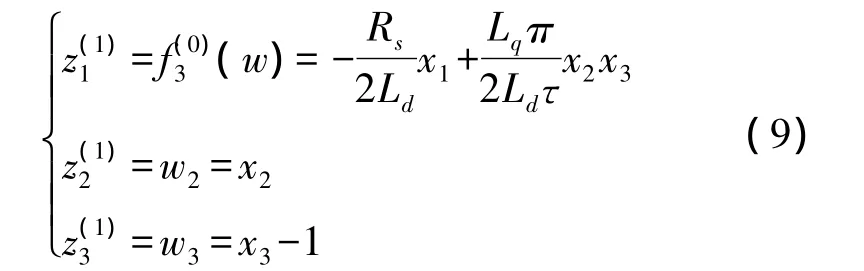
T的Jacobian矩阵为:

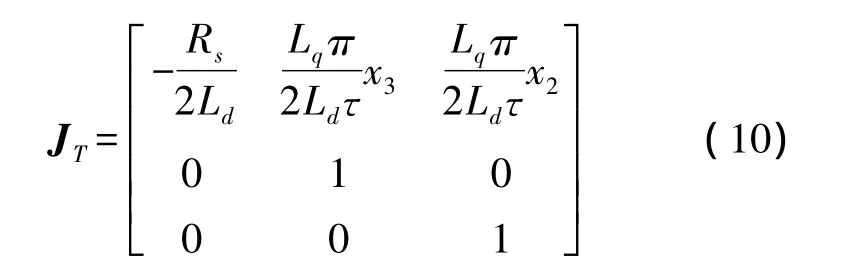
将T变换后，可求出最后一组变换，在该坐标变换下，原非线性系统的向量场 f(x)和 g1(x)、g2(x)可以重新写为:

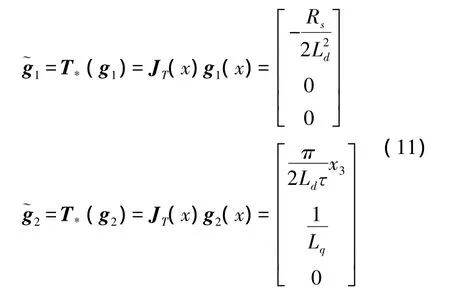
由此可得永磁同步直线电动机的非线性控制律为:

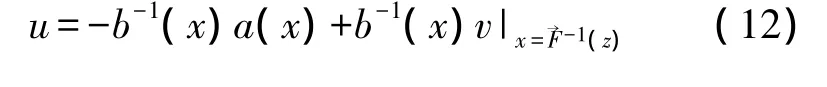
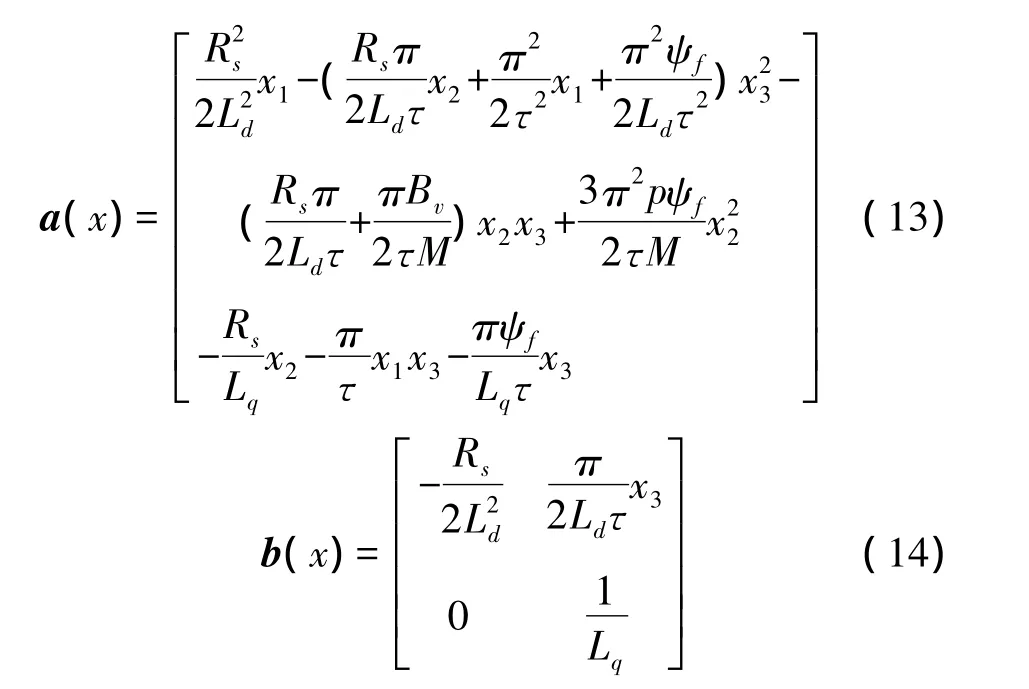
在新坐标及反馈变换下，永磁直线同步电机系统转化为线性系统:

它的Brunovsky标准型为:

3 最优控制器设计

通过求解ATP+PA-PBBTP+Q=0得出P*，通过K*=-BTP*求出K*，从而可得，永磁同步直线电动机系统的最优控制律v*为:

根据式(17)，可得永磁同步直线电机系统的非线性最优控制律为:

由式(9)可知:

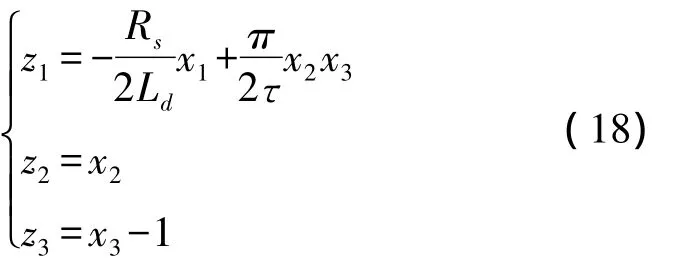
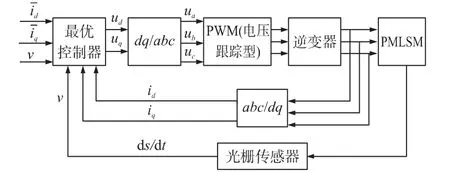
图2 控制系统结构原理图

基于微分几何的最优控制器结构如图2所示，以d、q动子电压作为输入，以d、q轴动子电流进行输出对最优控制器进行在线调节。

4 仿真及分析

为了验证微分几何最优控制动态性能的优越性，本文采用MATLAB对PMLSM系统进行实验仿真，永磁同步直线电动机的参数选取如表1。

为了对比分析，在相同参数及条件下，分别与传统PID控制进行仿真比较。当PMLSM空载起动时，阶跃响应参考线速度为1 m/s，在t=0.3 s时突加FΣ=120 N的负载阻力，Ld=Lq=120%L。通过反复的调节控制器的参数，使其达到了最佳效果，采用的微分几何最优控制器的参数为:k*1=0.87k*2=1.19。传统PID控制的参数为:kp=2.1，ki=3.6，kd=1.7。图3和图4为PMLSM系统在两种控制方法下参数变化前后的定子线速度响应曲线。

表1 实验数据参数表

图3 参数变化前定子线速度响应曲线

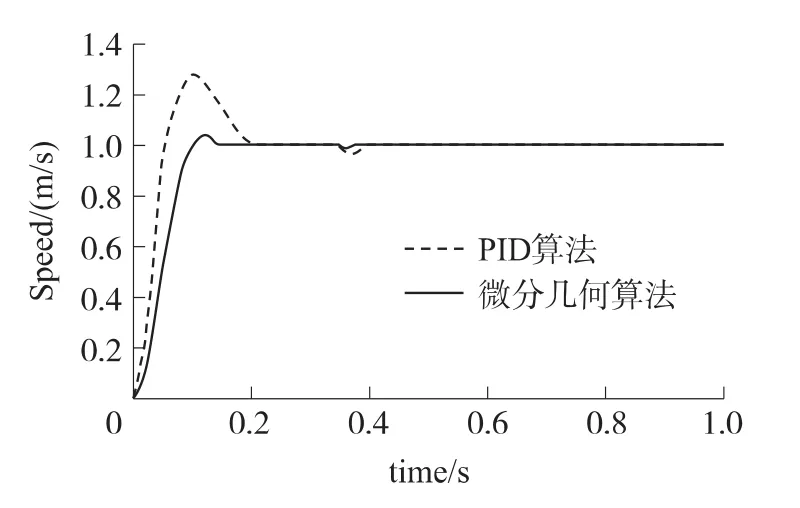
图4 参数变化后定子线速度响应曲线

通过对比参数变化前后的定子线速度响应曲线可以得出，在t=0.3 s时突加的负载阻力，基于微分几何的非线性最优控制方法对负载扰动的鲁棒性要明显的优于传统PID控制方法，参数的变化也对其影响较小。超调量较小，振荡也较小，其控制效果要明显优于传统PID控制。

5 结论

本文以PMLSM作为电梯的曳引驱动系统为背景，考虑其经常受到负载扰动、推力波动的影响。基于微分几何方法设计了稳定的最优控制器，改善了系统的跟踪性能，提高了系统的鲁棒性和控制精度。

［1］王华，邹积浩.基于模糊逻辑的直线永磁同步电机直接推力控制［J］.电子器件，2007，30(6):2279-2283.

［2］Tan S C，Lai YM，Tse CK.A Unified Approach to the Design of PWM-Based Sliding-Mode Voltage Controllers for Basic DC-DC Converters in Continuous Conduction Mode［J］.IEEE Trans on Circuit and Systems，2006.53(8):1816-1827.

［3］Jian Liu，Feng Qiao，Meiju Liu，et al.Neural Fuzzy Control to Minimise Torque Ripple of SRM［J］.Int J Modelling，Identification and Control，2010，10(1/2):132-137.

［4］孙宜标，魏秋瑾，王成元.永磁直线同步电机二阶滑模控制仿真研究［J］.系统仿真学报，2009，21(7):2037-2040.

［5］王武，白政民，姚宁.永磁直线同步电机神经滑模控制仿真［J］.电机与控制应用，2011，38(2):22-26.

［6］吴奎，高健，汪志亮，陈新.永磁同步直线电动机的自适应模糊滑模控制［J］.微特电机，2012，40(8):49-52.

［7］刘剑，孙成明，张大为等.变结构神经网络控制在SRD中的应用［J］.沈阳建筑大学学报(自然科学版)，2005，21(5):577-580.

［8］乔枫，张华，周悦等.滑模变结构控制在时滞系统中的应用［J］.沈阳建筑大学学报(自然科学版)，2009，25(2):399-403.

［9］Sira-Ramirez H J，Ilic M.A Geometric Approach to the Feed-Back Control of Switch Mode DC-to-DC Power Supplies［J］.IEEE Trans on Circuits on Systerns，1998，35(10):1291-1298.

［10］Knight J，Shirsavar S，Holderbaum W.An Improved Reliability Cuk Based Solar Inverter with Sliding Mode Control［J］.IEEE Transactions on Power Electronics，2006，21(4):1107-1115.

［11］Riccardo M，Patrizio T.非线性系统设计—微分几何、自适应及鲁棒性控制［M］.电子工业出版社，2006.

［12］王群，张桂香，陈杨等.双馈感应发电机的微分几何变结构控制方法研究［J］.机械制造与自动化，2009，38(6):133-136.

［13］桑建明，王亮，张世峰.基于微分几何方法的一种非线性控制器设计与仿真［J］.信息技术，2009，5(1):53-57.