基于改进粒子滤波的电力线载波通信语音增强*
崔恒志,王 翀
(江苏省电力公司信息通信分公司,南京210090)
电力线载波机利用输送电力的电缆线来传送话音及数据(远动信号),它在电力部门具有广泛的应用。根据有关约定,每4 kHz作为一个通道,高压电力线在40 kHz~500 kHz的频段内共分成115个信号通道。电力线两端的载波机利用两个不同频率的通道来发送本方和接受对方的信号。在一个通道内只传输一路话音和(或)一路数据的载波机称为单路载波机,而在一个通道内传输多于一路话音或数据信号的载波机称为多路载波机。单路载波机可以直接将模拟的话音信号和调制后的数据信号(通常采用FSK调制方式)合成一个4 kHz的信号通过功率放大后发送出去。多路载波机必须由话音/数据复接器将多路话音信号数字化压缩后,与多路数据一起打包调制发送出去。
语音增强是电力线载波机的一个重要组成部分,其主要任务是抑制背景噪声和干扰。电力线载波机在目标语音的实际拾取过程中,不可避免会受到外界环境噪声和其他说话人的干扰。如果干扰噪声过强对收听者而言则会觉得刺耳乃至听不清目标语音。针对这种情况,通常采用增强语音、去除背景噪声的方法来改善电力线载波机系统性能。在众多语音增强方法中,谱减法[1-2]是最常用的。但是其处理的语音会产生音乐噪声,而且在信噪比较低时残留噪声较大,不能得到很好的增强效果。另一类常见的语音增强方法是基于语音生成模型的方法,如卡尔曼滤波[3]。卡尔曼滤波的语音增强方法通过线性预测系数获得干净语音参数,并通过无语音帧获得噪声特性。当噪声是高斯过程时,卡尔曼滤波假设语音满足高斯分布,因此在对实际非高斯分布的语音的方面有其局限性。因而粒子滤波器也被用于语音增强。Vermaak[4]等人在采用语音的时变自回归(TVAR)基础上,提出一种基于Rao-Blackwellized粒子滤波的语音增强方法。金乃高[5]等到人在Vermaak算法的基础上通过子带分解降低了Rao-Blackwellized粒子滤波中采样空间的维数,达到减少计算量的目的。上述的两种方法在语音增强上获得了很好的效果,但是它们在建立语音的TVAR模型时未考虑模型的稳定性。此外,在选择重要性采样时将状态的先验分布作为建议分布进行状态估计,不能很好地逼近实际的后验分布,影响了估计精度,同时也导致了粒子的退化。本文提出了一种改进的基于粒子群优化的粒子滤波算法来进行语音增强,在分析语音信号TVAR模型的基础上对语音建模,引入粒子群优化的方法来产生建议分布,来近似估计未知状态变量的后验分布。使降噪结果更接近纯净语音,从而得到更好的语音增强效果。
1TVAR模型
实际语音信号处理中最常用的模型是自回归模型 AR(Autoregressive)[6],e(n)为激励信号,H(n)为全极点滤波器。该模型称为p阶自回归模型或AR(p)模型,其传输函数为:

假设语音和噪声信号相互无关,干净语音信号x(n)可以描述为一个由白噪声信号驱动、全极点线性自回归过程,将式(1)写成时域表达式,即:
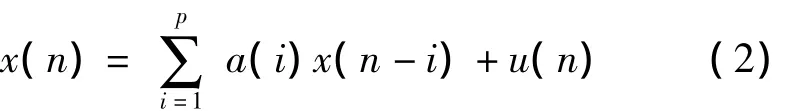
式(2)中,p为AR模型的阶数,{a(i)为AR模型的系数,u(n)为零均值且方差为的高斯白噪声。由式(2)可知,当前的测量值可以用过去的p个样本来进行预测,对于上述模型的参数估计通常使用的是线性预测分析的方法。首先对语音进行分段处理,当非平稳的段总是会出现,此时利用非平稳的信号模型,如TVAR模型,就可以对语音信号进行更好的跟踪,提供更加接近真实的估计。
TVAR模型可以认为是普通AR模型的扩展,其参数是时变的[7]。这其中包括激励源参数和声道模型参数,它们在短时间间隔内时变,为了更有效地描述语音信号的非平稳特性将式(2)改写成TVAR模型,即:
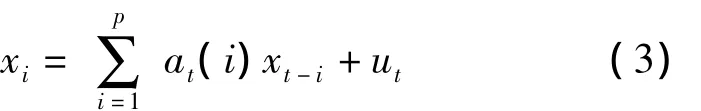
在此引入一个对数域偏差φut=lg(),并假设其变化规律满足高斯移动模型,则激励噪声的似然函数为在此,,α是小于1的系数。对于TVAR系数at(i)也采用高斯随机移动模型则有:
2 语音信号建模
语音信号xt和带噪的观测信号yt的TVAR模型如下:

式中,αt=(α1,t,α2,t,…,αp,t)T为t时刻p维的 AR系数矢量;et和vt为高斯白噪声,方差分别为σ2et和也是时变的。这样可以得到xt的条件概率密度为
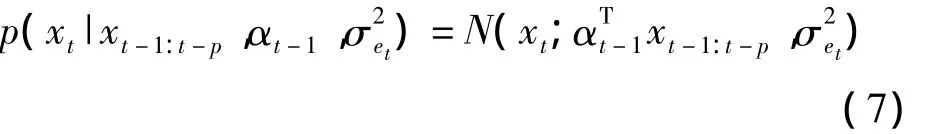
观测值yt的似然函数可以用均值为xt,方差为的正态分布加以描述
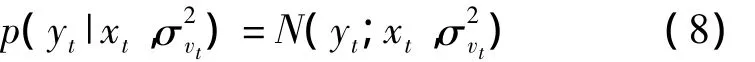
令Xt=(xt,…,xt-p+1)T,Yt=(y1:t),定义系统矩阵
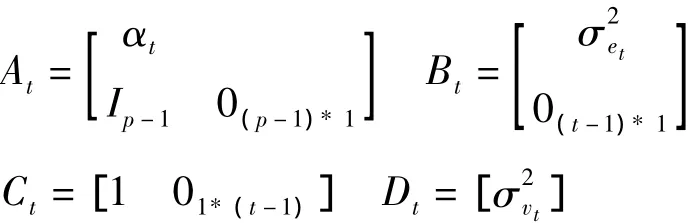
则语音信号模型可以表示为
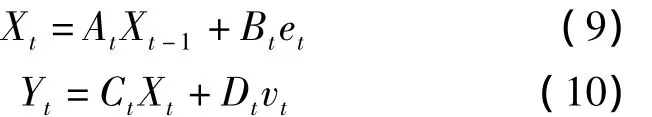
为了描述噪声{eti}和{vti}序列的时变特性,引入一个对数域的偏差,其对数域偏差的变化规律为高斯随机移动模型,即

这样,TVAR模型中的线性观测系数αt的时变特性描述最简单的方法也是使用高斯移动模型描述,即
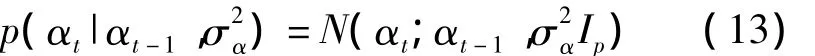
Ip为p阶单位矩阵。至此语音信号的TVAR模型已经完整定义了。上述所有的N(x;μ,σ2)均指变量x服从均值μ、方差σ2的高斯分布,未加说明的高斯分布均值为0。
信噪比是衡量针对宽带噪声失真的语音增强算法的常规方法。假设y(n)表示带噪信号,s(n)表示其中的纯净语音信号,s(^n)表示相对应的增强信号,所有这些信号都假设是能量信号,则时域误差信号为:
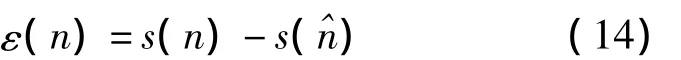
误差能量是:

纯净语音信号的能量是:

信噪比定义为:
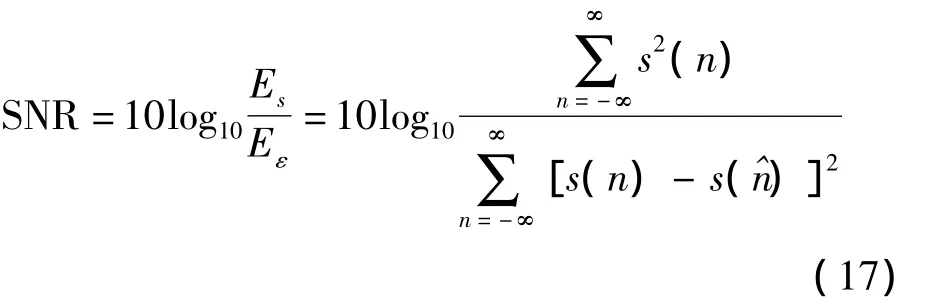
3 基于PSO-EPF粒子滤波的语音增强算法
基于语音参数模型的语音增强问题可以归结为从带噪语音y1:t={y1,y2,…,yt}中估计纯净语音x1:t={x1,x2,…,xt}的贝叶斯滤波问题,在此,我们利用粒子滤波器来实现对非线性非高斯序列的实时跟踪。
选取语音模型状态为
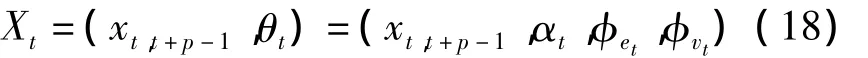
假设语音参数满足一阶马尔可夫随机过程p(Xt|Xt-1,Xt-2,…,X0)=p(Xt|Xt-1)
则上述状态变量的转移概率密度为
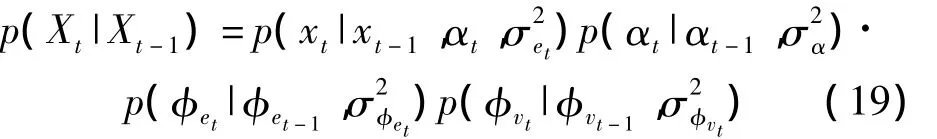
系统的观测模型为
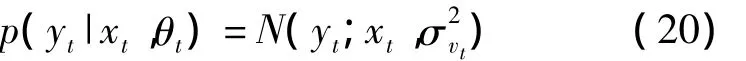
以下是基于改进粒子滤波的语音增强的算法流程:
(1)初始化
设置粒子数目N,指定N个初始权重,从先验分布p(X0)中采集粒子,其中,再设置粒子初速度,令=1/N;给定初始值 Δ^X0为常量;设置惯性权重λ,速度调节参数η,求解初始时刻全局最优解pg0
(2)重要性采样
①调整粒子的速度

②根据EKF算法对每个粒子状态进行更新,即在EKF算法重要性采样中将EKF算法重要性采样中状态k时刻的状态估计改为③求粒子集的均值和方差分别为和;
t;
⑤粒子权值更新
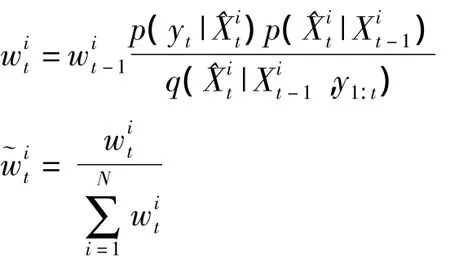
(3)重采样
消除权值较小的粒子,复制权值较大的粒子,当满足重采样条件时,获得N个随机样本,从近似服从分布p(X0:t|y1:t)为每一个再采样之后的样本粒子赋给相同的权值,即:当i=1,2,…,N,有=1/N。
(4)计算t时刻目标状态的后验概率估计Xt
(5)求解当前时刻全局最优解。
(6)t=t+1,返回重要性采样步骤,递推估计下一时刻的目标状态的后验概率。
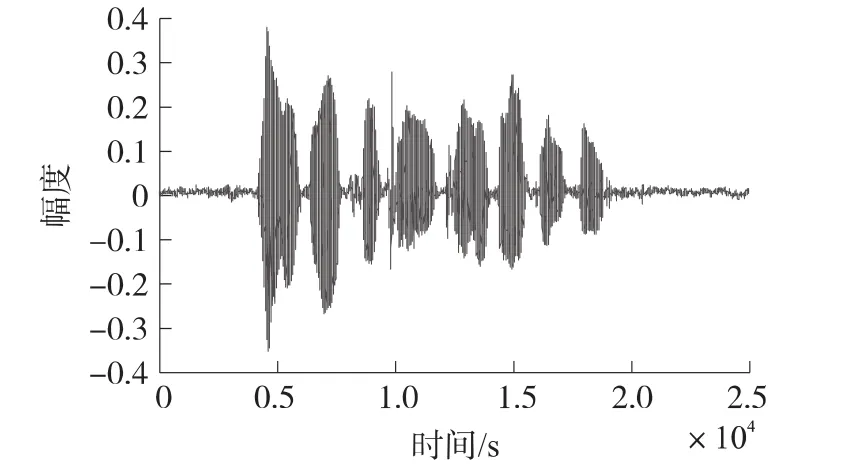
图1 纯净语音信号
4 实验仿真与结果分析
在本次实验中,分别利用EKF(Extended Kalman Filtering)算法、PF(Particle Filtering)算法、PSO-EPF(Particle Swarm Optimization-Extended Particle Filtering)算法对带噪语音信号进行增强,实验中,我们进行100次蒙特卡罗仿真。实验中采用的语音材料为自己录制,纯净语音为女声“人尽其才,团结合作”,噪声为录制的生活噪声,时长为2.5 s,语音和噪声信号经8 kHz采样、16 bit量化为数字信号,并在计算机中按一定比例混合生成不同信噪比的带噪语音,其信噪比变化范围为0~10 dB。使用的粒子滤波的粒子数为200,在实验中,TVAR模型的阶数为10,图1为纯净的语音信号,图2为带噪的语音信号,其初始信噪比为0.09 dB。
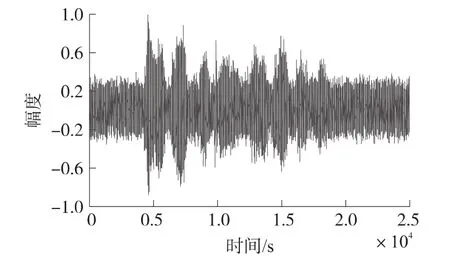
图2 带噪语音信号
在以上语音的基础上,使用MATLAB在PC上进行仿真实验,来比较带噪语音通过EKF算法、PF算法、PSO-EPF算法一次语音增强后的波形图(图3~图5)。由图3~图5可知,使用PSO-EPF算法处理后的带噪语音信号与纯净语音信号最为接近,也说明了它语音增强的效果最好。
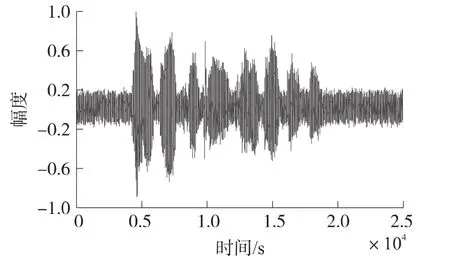
图3 EKF算法处理后的语音信号
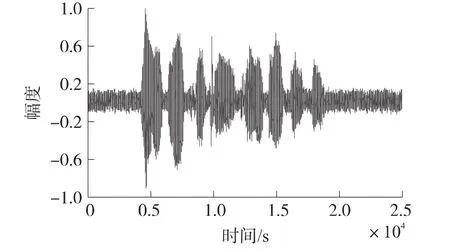
图4 PF算法处理后的语音信号
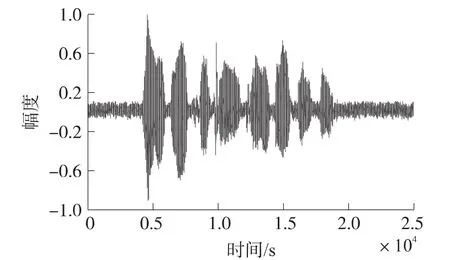
图5 EPF-PSO算法处理后的语音信号
下面从信噪比角度来说明,在不同的信噪比下,各种算法的语音增强效果如表1所示。

表1 不同方法和信噪比的语音增强效果
从表1可以看出,对于带噪语音信号,3种算法都能在一定程度上增强语音信号,表明TVAR模型可以很好描述语音信号的变化特性。而PSO-EPF算法对TVAR模型参数的估计能力比PF算法、EKF算法要有更好的效果,从而也具有更强的滤波降噪、增强语音的能力。
由前文可知,粒子数目对粒子滤波器的估计性能有很大的影响,因此我选择不同的粒子数来进行100次蒙特卡罗仿真,对带噪语音进行语音增强,输入信噪比设定在0.09 dB,增强效果如表2所示。

表2 不同粒子数的语音增强效果
由表2可见,随着粒子数目的增加,经过PF算法和PSO-EPF算法进行语音增强后,语音信号的信噪比得到增强,对TVAR模型参数的估计更加准确,但是增加粒子数目的同时,也将使得计算量增大[8]。所以,我们在选择语音增强算法时,要协调好粒子数目和SNR的关系,以便可以达到最好的语音增强效果。
5 结论
由于传统的基于粒子滤波语音增强算法不能很好地逼近实际的后验分布,影响了估计精度,同时也导致了粒子的退化。对此本文提出了一种基于粒子群优化的改进粒子滤波算法,它将语音增强问题转换为从带噪语音中对纯净语音的估计过程,引入粒子群优化的方法来产生建议分布,使降噪结果更接近纯净语音,从而得到更好的语音增强效果。
[1]Hu H T,YuC.Adaptive Noise Spectral Estimaton for Spectral Subtraction Speech Enhancement[J].Signal Processing,IET,2007,1(9):156-163.
[2]王振力,张雄伟.基于分数阶谱相减的语音增强方法[J].电子信息学报,2007,29(5):1096-1100.
[3]Kalman R E.A New Approach to Linear Filtering and Prediction Problem Trans[J].ASME J Basic Engineering,1960,82:34-45
[4]Vermaak J,Andrier C,Doucet A.Paticle Methods for Bayesian Modeling and Enhancement of Speech Signals[J].IEEE Transactions on Speech and Audio Processing,2002,10(3):173-185.
[5]金乃高,殷福亮.基于子带粒子滤波的一种语音增强方法[J].通信学报,2006,27(4):23-28.
[6]Lim J S,Oppenheim A V.A11—Pole Mmodeling of Degraded Speech[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1978,26(3):197-210.
[7]Grenier Y.Time—Dependent ARMA Modeling of Nonstationary Signals[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1983,1(4):899-911.
[8]赵力.语音信号处理[M].北京:机械工业出版社,2010.

