交叉张弦桁架预应力施工过程分析与索力实测
汤 磊 罗 斌 丁明珉
(东南大学土木工程学院,南京 210096)
预应力钢结构将高强拉索引入结构中,通过张拉拉索在结构中建立预应力,由于预应力改变了结构的内力状态和结构形状[1],因此,预应力钢结构的结构性能与普通钢结构相比存在较大差异.另外,由于预应力钢结构的施工相对于普通钢结构多一道预应力张拉工序,且大跨度预应力钢结构中拉索面广量大,无法实现整体一次性张拉到位,往往采用拉索分批、分级张拉的施工工艺,使得各施工工况下的结构状态与设计状态差别较大.由于上述预应力钢结构的结构性能和施工过程的特殊性,预应力钢结构施工的各个环节,从制作、安装到张拉,其结构受力性能均不同于普通钢结构工程[2].现阶段,通过有限元分析软件和国内部分学者自主开发的预应力钢结构设计与施工计算分析软件的应用,已经实现在预应力钢结构施工前对结构性能进行计算分析,并可通过模拟施工过程对各施工工况进行计算分析[3].
由于大多数预应力钢结构在其设计之初均为超常规结构,为验证理论分析方法的正确性和理论分析结果的可信度,以及验证预应力拉索施工方法的可行性和正确性等,需对预应力钢结构的拉索索力进行现场测试,常用的索力测试方法包括千斤顶压力表测定法[4]、压力传感器法、振动频率法[5]和磁通量测定法[6]等,其中基于拉索模态识别的振动频率法应用最为广泛且在不断地改进中.张宇鑫等[7]研究指出基于数值迭代求解方法识别张弦梁的索力精度无法保证.为提高精度及简化计算,文献[7]根据分析迭代计算得到的频率与索力相关关系的曲线和已有索力识别经验公式的特点,拟合出了基于索力频率测试结果的索力计算公式.文献[8]则在考虑减振装置的弹簧刚度对拉索边界条件的影响,着重研究减振装置弹簧刚度与等效索长的关系,提出考虑弹簧刚度影响的二次等效索长修正公式,并对该方法的误差敏感性、识别精度等进行了讨论.文献[9]给出了通过局部频率测试计算构件轴力的一种理论方法,并通过数值模拟和一系列实验验证了局部测试方法的正确性.文献[10]则结合预应力张弦结构的特点,根据已有研究成果提出了一种较为实用的张弦结构拉索索力平面外频率测试法,即通过测试张弦梁平面外拉索的频率,结合数值迭代和节点刚度修正,最终确定出拉索索力.本文以鄱阳湖模型试验研究基地后续工程模型试验大厅钢屋盖交叉张弦桁架为研究对象,结合施工全过程模拟分析结果,对其预应力实施全过程的索力测试结果进行了分析研究.
1 工程概况
鄱阳湖模型试验研究基地后续工程模型试验大厅钢屋盖采用交叉张弦桁架结构,预应力交叉张弦桁架共11榀,每榀预应力交叉张弦桁架由“X形”上弦桁架通过拉索及撑杆组成一榀空间预应力钢桁架,见图1(a).张弦桁架跨度110 m,中心间距15 m,截面高度11 m.上部桁架为变截面倒三角形立体钢管桁架,桁架高度从中部的3 m渐变为边部的2 m,桁架宽度从中部的2 m渐变为边部的1.4 m,见图1(b).
张弦桁架一端固定铰接于一侧混凝土柱边的框架梁顶,另一端设置单向滑动铰支座支承于另一侧混凝土柱边的框架梁顶.张弦桁架平面外设置适当数量的支撑桁架.张弦桁架支座处节点采用铸钢节点,桁架杆件间连接采用相贯线焊缝.该张弦桁架的拉索索体采用强度等级为fptk=1 670 MPa的φ7 mm高强度低松弛镀锌钢丝半平行钢丝束,拉索规格为φ7 mm×127,拉索理论张拉力为1 100 kN,索体两端可调.张拉端锚具采用冷铸镦头锚,且端部设置高阻尼黏弹性橡胶减震圈.
2 预应力施工分析
2.1 张弦桁架张拉时机的选择
选择合适的时机进行预应力张拉不仅可以建立有效的预应力值而且可以减少张拉的工作量.对鄱阳湖模型试验研究基地后续工程模型试验大厅钢屋盖的交叉桁架预应力拉索张拉采用荷载子步分析方法,对在支撑胎架上的单榀张弦桁架和整体结构分别进行了预应力拉索分级张拉的全过程分析,具体分级见表1,分析结果见图2.采用大型通用有限元分析软件ANSYS进行结构在支撑胎架上预应力拉索分级张拉的全过程分析.桁架部分采用梁单元Beam188, 撑杆采用两端铰接的杆单元Link8,拉索采用只受拉、不受压和不受弯的索单元Link10,支撑胎架采用仅受压、不受拉和不受弯的单元Link10.支座一端铰接,一端沿拉索张拉方向单向滑动铰接.材料弹性模量:钢材取206 GPa,拉索取195 GPa.荷载取结构自重标准值.为计算精确,分析中考虑应力刚化效应和几何非线性,采用Newton-Raphson方法迭代求解.
由分析结果可得,当索力张拉力达到约800 kN时,单榀交叉张弦桁架基本脱离了支撑胎架,而整体结构在索力达到1 000 kN时仍未脱离胎架.分析结果表明,采用单榀张弦桁架张拉,在较小的张拉力下桁架即可脱离胎架,可避免整体结构逐榀张拉时由于先后张拉顺序而导致的索力相互影响.此外,由图2可得在单榀张弦桁架张拉时,当索力平衡结构自重,桁架刚脱离支撑胎架后,竖向位移受张拉力影响非常敏感,因此在实际施工中,不仅要控制张拉力还要严格监控竖向位移.
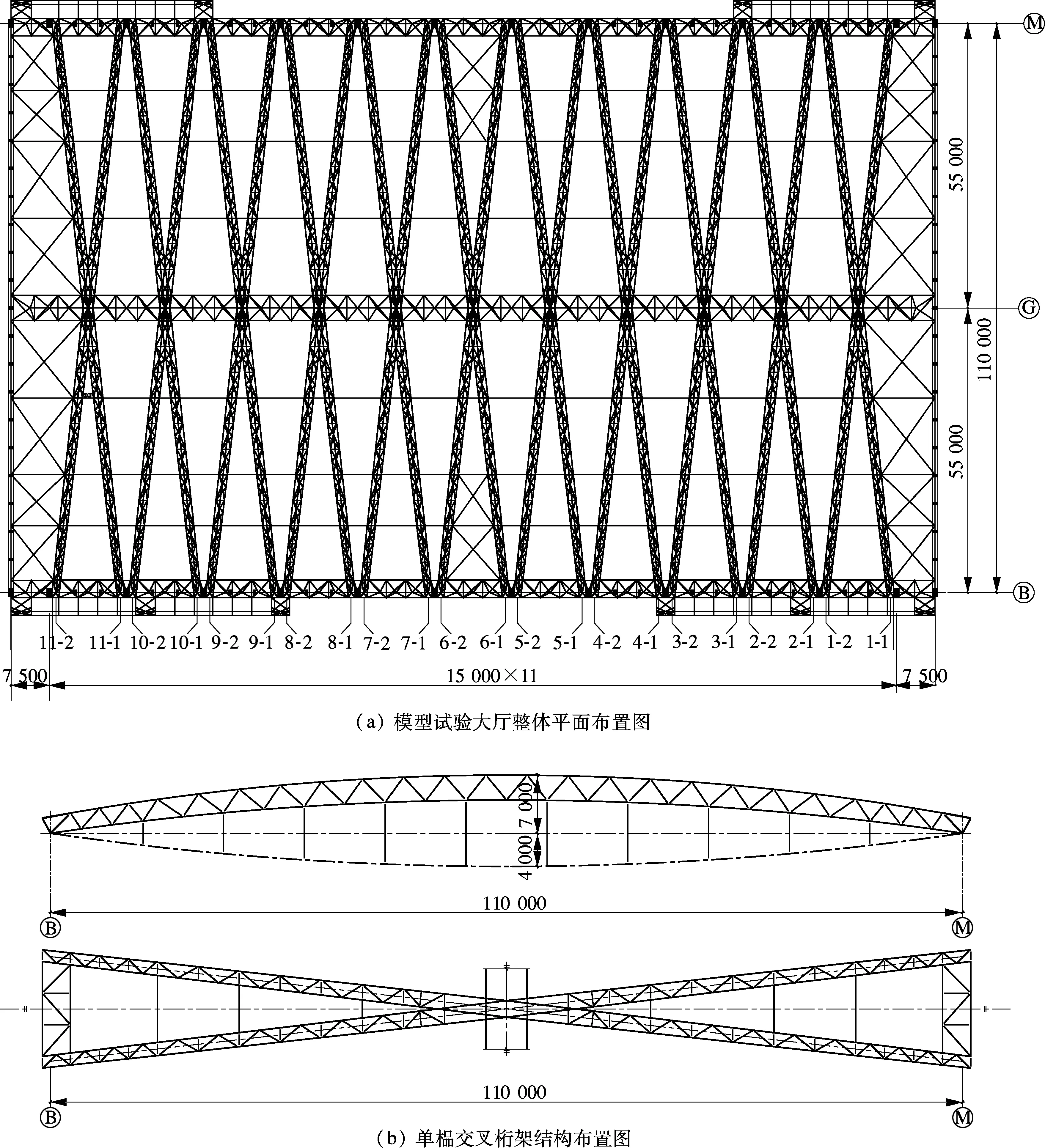
图1 模型试验大厅结构图(单位:mm)

表1 预应力拉索分级张拉索力
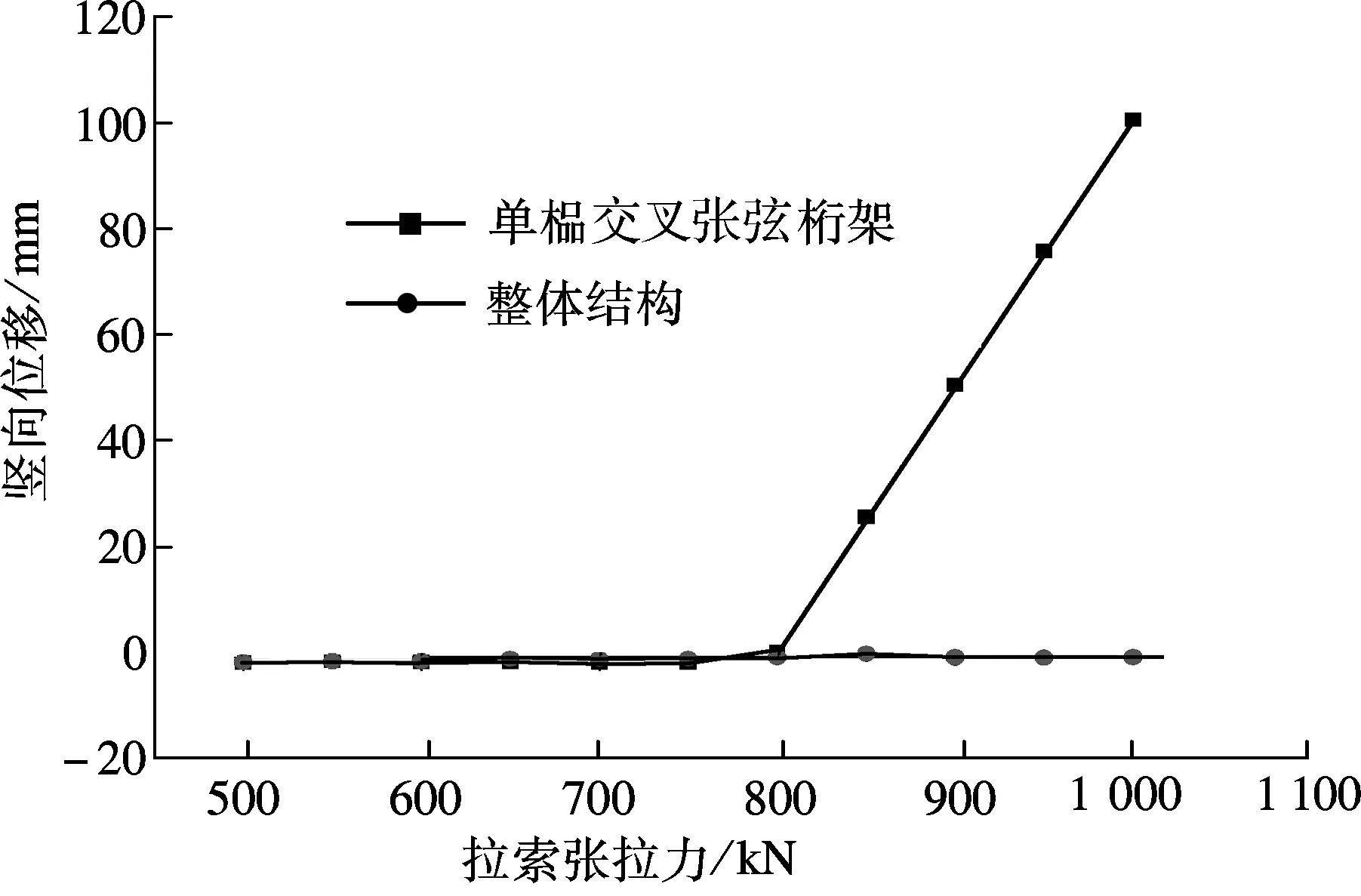
图2 拉索张拉力-结构竖向位移的变化曲线
2.2 单榀桁架与整体结构稳定性分析
相对整体结构逐榀张拉,单榀交叉张弦桁架独立张拉时的侧向稳定性较差,因此通过特征值屈曲分析进行稳定性验算.考虑到结构的非线性,取在拉索等效预张力、结构自重共同作用下的结构平衡态的刚度作为特征值屈曲分析的刚度矩阵.计算结果见表2和图3.
由分析结果可得:① 前4阶模态特征值,单榀交叉张弦桁架明显低于整体结构,但第5阶及之后两者的特征值比较接近.② 单榀交叉张弦桁架的最低阶屈曲荷载数为11.322,说明其仍具有良好的稳定性,单独张拉不会出现侧向失稳.

表2 单榀交叉张弦桁架和整体结构的前10阶屈曲荷载系数
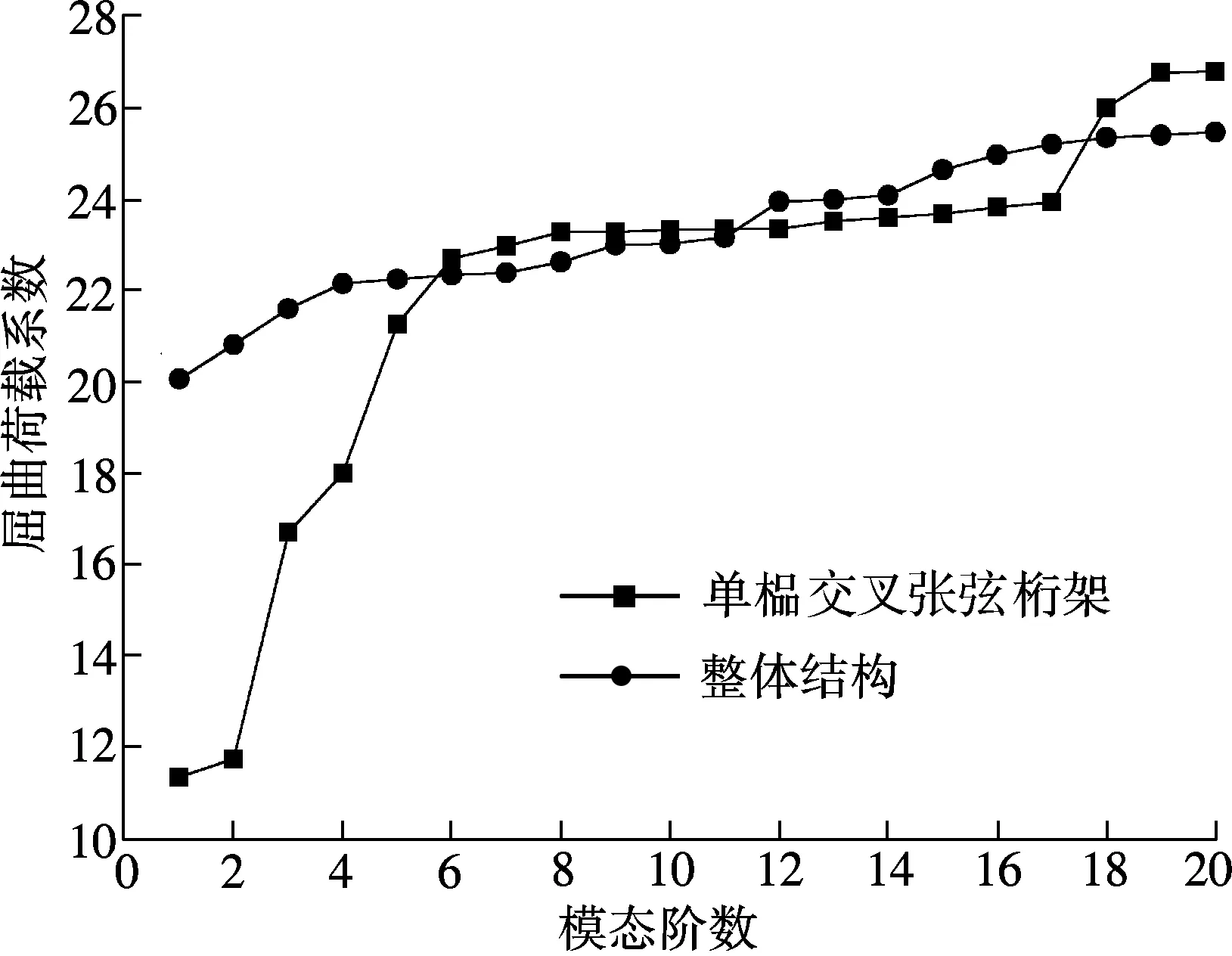
图3 单榀桁架和整体结构屈曲荷载系数曲线
3 索力测试与对比分析
拉索预张力施工过程是个动态的结构状态变化过程,是结构从零状态向成形初始态转变的过程.由于钢构件安装误差、拉索制作、安装和张拉误差、分析误差以及环境影响等因素,实际结构状态与分析模型有一定差异的.因此,有必要对拉索预应力施工过程予以监测,对比理论分析值和实际结构响应的差异,及时掌握各关键施工阶段的结构状态,保证拉索施工全过程处于可控状态,为下阶段施工和最后的施工验收提供依据.
3.1 监测内容和方法
工程共11榀交叉张弦桁架,共计22根拉索.对拉索索力的监测共分2次进行:① 考虑到采取的是单榀交叉桁架张拉方法,因此预应力施工过程中选择预应力张拉完成屋面檩条未安装时进行索力测试,校验千斤顶张拉力的精度.② 在纵向连系桁架安装完成,整体屋盖结构成型后,对所有拉索(22根)的索力进行测试,以便掌握整体结构成型时的索力状况,桁架和拉索编号见图1(a).该工程分别选择频率法来测试所有拉索的索力,压力传感器法测试第5榀和第6榀桁架的拉索索力,如图4所示.

图4 拉索索力测试方法
3.2 平面外的频率法测试步骤
该工程索力测试采用平面外自振频率法测试平面索杆系拉索索力.该方法通过将平面索杆系中的连续短索转化为平面外的长索,通过实测平面外自振频率和建立索力-平面外自振频率的关系来确定拉索索力.具体步骤为:① 进行平面索杆系有限元模型的模态分析,确定平面外计算长度;② 实测平面索杆系的平面外自振频率;③ 根据实测的多阶平面外自振频率,识别平面外抗弯刚度;④ 建立索力-平面外自振频率的关系;⑤ 计算索力.其中,拉索索力T可根据测得频率进行计算,其计算式为[11]
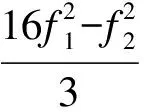
(1)
式中,m为索的线密度(可以通过产品规格查得);f1,f2分别为第1阶和第2阶自振频率(可以通过频率计测得);l为拉索计算长度.由于拉索端部的约束比较复杂,因此,拉索计算长度l的确定成为实际工程测量的难点.
该工程的拉索规格为φ7 mm×127,钢丝束外接圆直径为91 mm(不含外包PE厚度),被撑杆划分的索段长度约为11 m,索段长度与索体直径之比为120.9.与斜拉结构相比,张弦桁架撑杆间各索段较短,索段两端约束条件复杂,无法直接确定拉索计算长度,因此,通过在索头布设压力传感器,对两榀桁架的拉索索力进行校对来确定其计算长度.
3.3 压力传感器和频率法索力测试结果
对拉索5-2和6-1采用压力传感器和频率计进行索力校核测试.由压力传感器测试的索力见表3.
假定各测试索段的计算长度系数相等, 根据式(1)可得出本工程频率法索力测试的平均计算长度系数为0.974.由于计算长度系数约等于1,说明撑杆下端对拉索的约束作用近似固定铰接.具体计算步骤如下:

表3 压力传感器测试的索力 kN
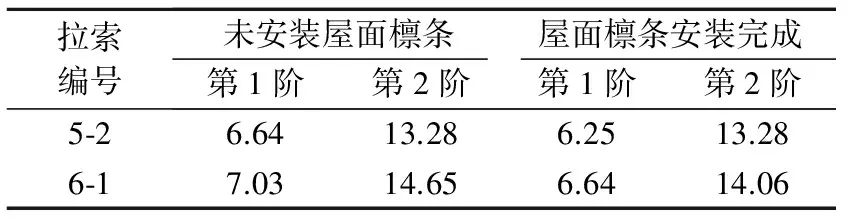
表4 频率法测得索段振动频率 Hz
通过修正索段的计算长度,得出频率法测试索力结果,如表5和表6所示.测试结果表明:在拉索张拉完成和安装屋面檩条后,测试索力与理论值的偏差在±10%以内,因而符合设计要求.

表5 屋面檩条未安装时的各索索力测试结果
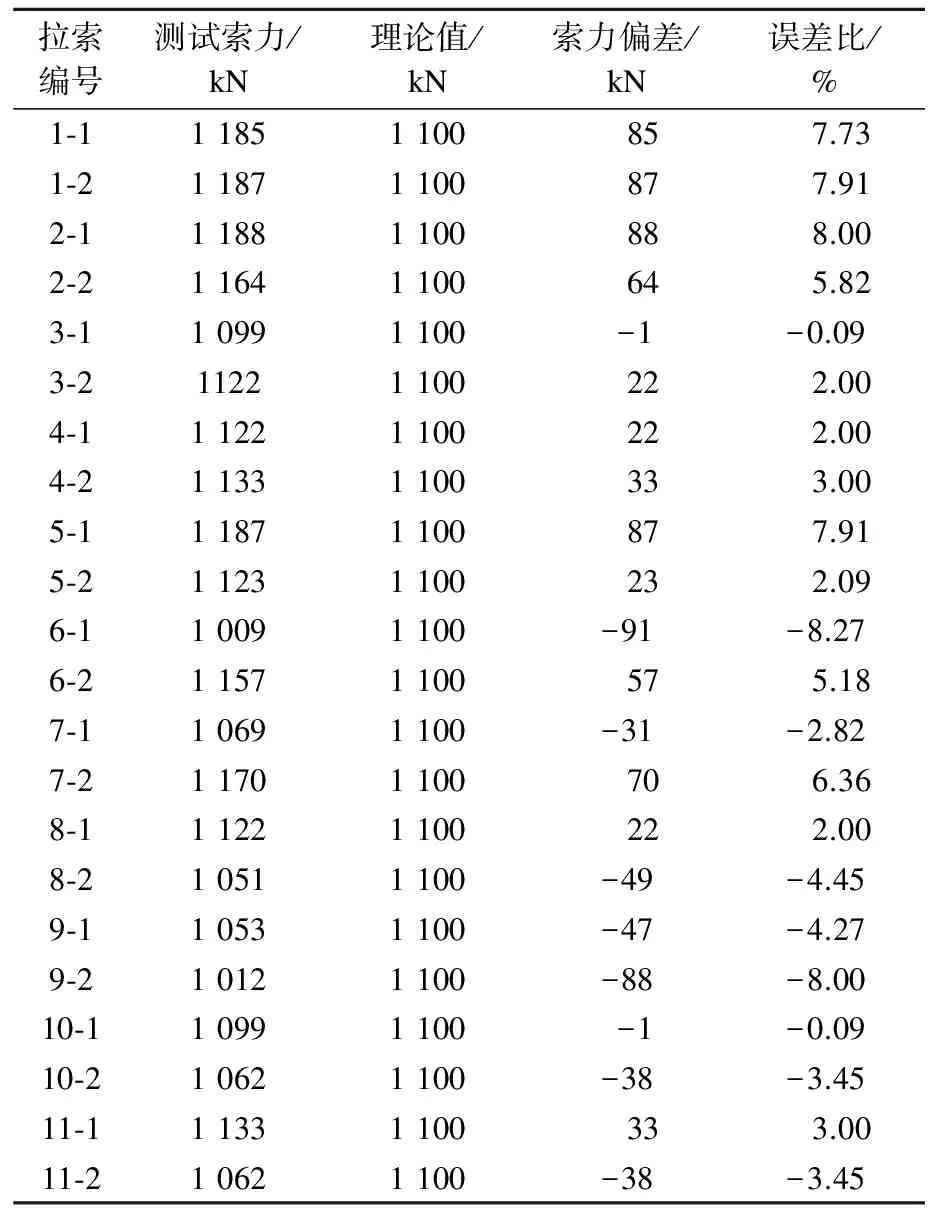
表6 屋面檩条安装完成的各索索力测试结果
4 结论
1) 本工程采用单榀交叉桁架张拉方法是切实可行的,张拉时索力控制分为11级是合理的.实测表明,张拉过程中索力与理论分析相符,张拉完成后结构状态满足设计初始态的要求.
2) 单榀交叉张弦桁架具有良好的平面外稳定性,独立张拉不仅脱架时的拉索张拉力较小,而且可避免各榀间先后张拉导致的索力相互影响,因此对交叉张弦桁架采用单榀独立张拉是合理的.
3) 由于张弦桁架的索段长度短,采用频率法测试索力时,通过取前两阶自振频率计算索力来考虑索体抗弯刚度的影响,另通过压力传感器测试索力修正计算长度来考虑索端约束刚度,可达到较好的测试精度.
4) 本工程采用频率法索力测试的计算长度系数为0.974<1,说明撑杆下端对拉索的约束作用近似固定铰接,因此对计算长度的修正是必要的.
)
[1] 董石麟,罗尧治,赵阳,等.新型空间结构分析、设计与施工[M].北京,人民交通出版社,2007:506-531.
[2] 王永泉,郭正兴,罗斌,等.空间预应力钢结构拉索等效预张力确定方法研究[J].土木工程学报,2013,46(6):53-61.
Wang Yongquan, Guo Zhengxing, Luo Bin, et al. Study on the determination method for the equivalent pre-tension in cables of spatial prestressed steel structure[J].ChinaCivilEngineeringJournal, 2013,46(6): 53-61.(in Chinese)
[3] 卓新,袁行飞.预应力索分批张拉过程中张力的仿真分析[J].土木工程学报, 2004,37(9):27-30.
Zhuo Xin, Yuan Xingfei. Emulational analysis of the tensile forces of prestressed cables during multistage tensioning construction[J].ChinaCivilEngineeringJournal, 2004,37(9): 27-30. (in Chinese)
[4] 段波,曾德荣,卢江.关于斜拉桥索力测定的分析[J].重庆交通学院学报,2005, 24(4):6-8,12.
Duan Bo, Zeng Derong, Lu Jiang. Analysis with determining cable tension of cable-stayed bridges[J].JournalofChongqingJiaotongUniversity, 2005,24(4): 6-8, 12. (in Chinese)
[5] Kim Byeong Hwa, Park Taehyo. Estimation of cable tension force using the frequency-based system identification method[J].JournalofSoundandVibration, 2007,304(3/4/5): 660-676.
[6] 陈鲁,宋杰,张其林.EM法测量索张力的理论与工程实践研究[J].施工技术, 2008,37(5):144-153.
Chen Lu,Song Jie,Zhang Qilin. Theory and engineering practice research on cable tension measurement with EM method[J].ConstructionTechnology, 2008,37(5): 144-153. (in Chinese)
[7] 张宇鑫,李国强,赵世峰.张弦梁结构振动方法索力识别(Ⅱ):实用公式及误差分析[J].振动与冲击,2009,28(3):158-160,181.
Zhang Yuxin, Li Guoqiang, Zhao Shifeng. Vibration-based cable tension identification of a beam string structure (Ⅱ): practical formula & error analysis[J].JournalofVibrationandShock, 2009,28(3): 158-160, 181. (in Chinese)
[8] 黄侨,胡健琛,黄志伟,等.考虑减振装置弹簧刚度的斜拉索等效索长及索力测量[J].东南大学学报:自然科学版,2012,42(4):724-728.
Huang Qiao, Hu Jianshen, Huang Zhiwei, et al. Equivalent length of stayed-cable considering spring stiffness of damping device and measurement of cable-force[J].JournalofSoutheastUniversity:NaturalScienceEdition, 2012,42(4): 724-728. (in Chinese)
[9] Maes K, Peeters J, Reynders E, et al. Identification of axial forces in beam members by local vibration measurements[J].JournalofSoundandVibration, 2013,332(21): 5417-5432.
[10] 潘杰,罗斌,郭正兴.东南大学九龙湖体育馆轮辐式张弦梁结构施工技术研究[J].施工技术,2012,41(375):65-67,102.
Pan Jie, Luo Bin, Guo Zhengxing. Beam string structure construction study of the southeast university gymnasium[J].ConstructionTechnology, 2012,41(375): 65-67, 102. (in Chinese)
[11] 刘文峰,应怀樵,柳春图.考虑刚度及边界条件的索力精确求解[J].振动与冲击,2003,22(4):12-14,25.
Liu Wenfeng, Ying Huaiqiao, Liu Chuntu. Precise solution of cable tensile force in consideration of cable stiffness and its boundary conditions[J].JournalofVibrationandShock, 2003,22(4): 12-14, 25. (in Chinese)

