基于基因扰动及变分逼近技术的基因调控网络推断

董自健 宋铁成 袁 创

(1东南大学信息科学与工程学院, 南京 210096)(2淮海工学院电子工程学院, 连云港 222005)(3香港理工大学医疗科技及信息学系, 香港)

基因调控网络(GRN)结构的推导对理解基因功能和复杂疾病的致病原因至关重要．基因调控网络的推断需要识别出基因之间的相互作用,而仅使用实验方法确定基因之间的相互作用需要进行大量的实验．由于计算技术和计算能力的快速提高,现在通常不是单纯使用实验手段,而是根据有限的实验数据,使用统计方法推断基因调控网络．

由于引入了扰动信息,基因扰动技术可有效提高GRN推断的精度．基于基因表达数据,可以把基因调控网络建模为图结构[1], 其中基因用节点表示,节点之间的边表示基因之间的调控关系．另外高斯图模型[2]、线性回归模型等[3]都可以用于基因调控网络的推断．但这些方法的准确度都不高．结构方程(SEM)模型也可用于推断基因调控网络[4-5],如Logsdon等[5]使用SEM对基因网络进行建模,并使用Adaptive Lasso (AL-based)算法推导网络参数．通过仿真,作者认为AL-based算法优于已有的其他各种算法．

基于基因表达和eQTLs数据,本文把基因调控网络建模为SEM结构．由于这2类数据均已知,故不存在潜变量,因此本文把SEM模型转化为验证性因子分析(CFA)结构,并进而简化为线性回归模型．为降低算法对数据的敏感性,本文使用贝叶斯推断方法代替常用的最大似然以及各种Lasso方法求解线性回归模型;为了降低计算量,不使用通常的马尔科夫-蒙特卡洛(MCMC)方法,而是采用变分逼近方法(VAM)进行贝叶斯推断．仿真结果表明CFA模型和VAM算法都是有效和可靠的．VAM算法的性能较好,在误检率和检测率上都远高于AL-based算法;与最大似然等方法相比,变分逼近方法无需准确估计初始参数，对数据适应性较好．

1 基因网络结构的CFA模型

假设有Ng个基因,Nq个标记,N个测量样本．基因网络结构服从如下结构方程模型:

Y=AX+BY+ε

(1)

式中,Y为Ng×N矩阵,其中ykj为基因k在第j次测量中所获得的表达数据;B为Ng×Ng矩阵,包含所有的网络参数;X为Nq×NeQTLs数据矩阵,Nq≥Ng；A为Ng×Nq矩阵,表示每个eQTLs对每个基因的影响;ε为Ng×N矩阵,其中εkj表示第j次测量中基因k的表达误差．

假设基因自身不存在相互作用,因此矩阵B的对角元素值为0．另外,假设所有的eQTLs位点已根据已有的方法确定出来,但是每个eQTLs的影响未知,因此A中有Nq个位置已知的未知参数,剩下的NgNq-Nq个元素都是0．不失一般性,假设Ng=Nq．

式(1)中所有未知参数都在B和A中,因此模型可变为

Y=ΛΩ+ε

(2)

式中,Λ=[BA],Ω=[YX]T．现在模型已变为一类特殊形式的SEM模型,即CFA模型．将式(2)作如下分解:

(3)

由于已知数据均在Ω和Y中,所以可逐行求解Λ中参数,因此问题分解为

Yk=ΛkΩ+Υkk=1,2,…,Ng

(4)

2 CFA模型的变量逼近推断

假设Λ矩阵稀疏,即Λ中大部分数据为0,因此可假设Λ中所有参数服从均值为0的高斯分布,且Υk服从N(0,σ2I)．

将式(4)转化为

(5)

式中,Ωj为Ω的第j行参数,D=2Ng．现在问题转化为一个标准的线性回归问题．如前所述,在贝叶斯推断中,如果采用MCMC方法,在变量较多的情况下,计算量将非常大．因此本文使用变分逼近替代MCMC方法用于网络调控参数的推断．变分逼近技术已得到很多应用,如Logsdon等[6]和Carbonetto等[7]把该方法用于多位点的基因组关联分析．

2.1 调控参数后验概率计算

根据变分理论[8],限制p(θ|Ω,Yk,υ(m))≈q(Λk,Zk),且q(Λk,Zk)可分解为

(6)

其中,每个分项可表示为如下形式[9]:

(7)

根据变分逼近理论可得出迭代参数为[7,10]

(8)

(9)

(10)

2.2 基于重要性抽样技术的包含概率计算

为考察基因k和基因j之间的关系,还需判断每个参数(Λkj)是否包含在模型中,即计算

(11)

该积分计算非常复杂,需要近似计算．已知p(zkj=1|Ω,Yk,θ)=αkj,为了计算Λkj是否包含在模型中,需要根据式(11)计算其后验概率．这里使用重要性抽样,即

(12)

式中,w(υ(m))为重要性抽样系数,

(13)

式(13)中的p(Yk|Ω,υ)很难计算,Carbonetto等[7]使用Jessen不等式获得了其下界:

(14)

式中,αk.×μk表示αk和μk两个行向量的点乘．在计算时可使用这个下界代替p(Yk|Ω,υ)．

(15)

算法具体过程如下:

输入:X,Y,抽样样本序列{sπ,sσ,sΛ},以及α(0),μ(0),ξ．

1 根据式(2)计算Ω;

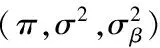
3 fork=1∶Ng(对调控参数矩阵逐行求解)

form=1∶M

置υ=υ(m);令flag=1;根据式(8)计算s2;

while flag

forj=1∶D

根据式(9)、(10)分别更新μkj和αkj

endj;

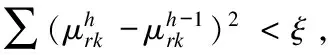
end while

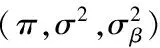
endm

根据式(13)、(14)获得重要性系数w(υ(m));

根据式(12)获得后验概率p(zkj=1|Ω,Yk);

根据式(15)计算调控网络参数Λk;

endk

3 仿真结果

本文分别仿真了含有30个基因的有向无环和有向有环网络．每个基因节点平均有3条边,即NE=3．如果从节点j到节点k有边,则从(-1,-0.5)∪(0.5,1)中均匀抽样;否则Bkj置为0．eQTL中每个xij以概率(0.25,0.5,0.25)从集合 {1,2,3}中抽取．测量噪声服从N(0,0.1)分布．不失一般性,设A为单位阵．Y通过式 (1)计算获得．在仿真中,如果算法返回的p(zkj=1|Ω,Yk)>0.95,且Λkj>0.10,则认为从节点j到节点k之间有一条边,其他情况均判为2个节点之间无调控关系．

本文主要与AL-based算法在检测率和误检率上进行性能比较,图1给出了仿真结果．可以看出,在检测率和误检率2个方面,VAM算法均优于AL-based算法．

图1 VAM算法在30个基因调控网络中的性能

4 酵母基因调控网络的推断

本节使用VAM算法对一酵母基因网络进行推断．数据来自对酵母菌株BY4716和RM11-1A进行交叉实验所获得的112组基因表达数据,以及基因标记数据[11]．数据中共包含5727个基因．由于测量数据样本有限,且存在一定的误差,不可能用这些数据较为准确地推断出全部5727个基因之间的调控关系,因此需要使用预处理技术,选择具有较强表达数据差异的基因进行分析[5]．本文采用Logsdon等[5]提供的经过预处理的基因表达数据以及相应的eQTLs数据进行网络参数推导．这些数据共包含35个基因的相关测量数据,具体酵母基因名称见图2．

图2 部分酵母基因调控网络结构图

所推导的调控网络结构如图2所示．其中8个基因与其他基因之间没有相互关系,其他27个基因之间有43条有向边．实线表示基因之间是正调控,共18条,其中ORC5与NUP60之间有相互作用的正调控;虚线表示负调控,共25条边．

为了验证算法推导的结果,本文使用YEASTRACT网站的Generate Regulation Matrix工具[12],得到了包含上述35个基因的调控网络图,其中包含3个基因调控对,分别是HAL9调控HIM1[13], PHD1调控YEL073C[13],PHD1调控FYV6[14],这些基因调控关系都经过已有实验验证．VAM算法推导出的43条边中,包含了HAL9调控HIM1和PHD1调控YEL073C这2组调控关系对．

5 结语

本文把基因调控网络建模为没有潜变量的验证性因子分析模型,并把模型分解为线性回归模型,逐行求解．在处理线性回归模型时,首先采用变分逼近技术推导参数的后验概率分布,在此基础上,使用重要性抽样技术计算参数包含在线性模型中的后验概率,并得出网络参数的加权平均．将VAM算法与AL-based算法进行比较,验证了VAM算法的有效性和可靠性．最后使用实验数据,针对一种酵母基因调控网络进行了推导,得出了一个具有43条边的参考基因调控网络结构．

)

[1] Friedman N. Inferring cellular networks using probabilistic graphical models [J].Science, 2004,303(5659):799-805.

[2] Schafer J, Strimmer K. An empirical Bayes approach to inferring large-scale gene association networks [J].Bioinformatics, 2005,21(6):754-764.

[3] Schafer J, Strimmer K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics [J].StatisticalApplicationsinGeneticsandMolecularBiology, 2005,4(1):1175-1189.

[4] Xiong H, Choe Y. Structural systems identification of genetic regulatory networks [J].Bioinformatics, 2008,24(4):553-560.

[5] Logsdon B A, Mezey J. Gene expression network reconstruction by convex feature selection when incorporating genetic perturbations [J/OL].PLoSComputationalBiology,2010,6(12). http://www.ploscompbiol.org/article/info%3Adoi%2F10.1371%2Fjournal.pcbi.1001014.

[6] Logsdon B A, Hoffman G E, Mezey J G. A variational Bayes algorithm for fast and accurate multiple locus genome-wide association analysis [J/OL].BMCBioinformatics, 2010,11. http://www.biomedcentral.com/1471-2105/11/58/.

[7] Carbonetto P, Stephens M. Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies [J].BayesianAnalysis, 2012,7(1):73-107.

[8] Jordan M I, Ghahramani Z, Jaakkola T S, et al. An introduction to variational methods for graphical models [J].MachineLearning, 1999,37(2):183-233.

[9] Attias H. Independent factor analysis [J].NeuralComputation, 1999,11(4):803-851.

[10] Beal M J. Variational algorithms for approximate Bayesian inference [D]. London: University of London, 2003.

[11] Stranger B E, Forrest M S, Dunning M, et al. Relative impact of nucleotide and copy number variation on gene expression phenotypes [J].Science, 2007,315(5813):848-853.

[12] Knowledge Discovery & Bioinformatics Research Group.YEASTRACT [EB/OL]. [2013-03-10]. http://www.yeastract.com/index.php.

[13] Lee T I, Rinaldi N J, Robert F, et al. Transcriptional regulatory networks in Saccharomyces cerevisiae [J].Science, 2002,298(5594):799-804.

[14] Borneman A R, Leigh-Bell J A, Yu H, et al. Target hub proteins serve as master regulators of development in yeast [J].GenesandDevelopment, 2006,20(4):435-448.