证据权模型中两种预测单元划分方式对比

张道军，成秋明，左仁广

1.中国地质大学地质过程与矿产资源国家重点实验室，武汉 430074

2.中国地质大学资源学院，武汉 430074

3.中国地质大学地质过程与矿产资源国家重点实验室，北京 100083

0 引言

自国际地球科学联合会1978年推荐6种矿产资源定量预测方法以来［1］，各种方法被引入到矿产资源定量预测与评价。这些方法可归为数据驱动和知识驱动两大类：数据驱动模型如证据权［2－3］、神经网络［4－6］、贝叶斯网络分类器［7］和支持向量机［8］，该模型主要是研究矿床（点）与多源找矿信息的关系，通过定量分析建立起区域成矿的后验概率、成矿有利度等与多参数地质信息的统计规律，根据数学模型进行资源潜力评价；知识驱动模型，如布尔逻辑［9］、二值图层叠加［9］、多值图层叠加［9］、模糊逻辑［10］、证据理论［11］等，是通过综合勘查资料，研究区域矿床成矿规律，系统而全面地考察矿床形成机制、控矿因素和找矿标志，根据地质和已有经验对地质变量赋值，进而圈定预测远景区。

证据权方法是一种基于贝叶斯定理的数据驱动方法，20世纪80年代加拿大Agterberg和Bonham－Carter等数学地质学家将其引入到矿产资源预测与评价［2，12－14］。证据权模型具有结构清晰和易于理解等特点［14］，因而成为目前使用最为广泛的矿产预测与评价方法之一。对该模型本身的研究一直是国际数学地球科学协会研究的热点。成秋明等提出了基于分形理论的证据权法［15］和模糊证据模型［16］；Journel［17］从如何解决数据冗余角度提出了Tau模型；Krishnan［18］对 Tau模型进行了发展；Porwal等［7］在模糊证据权方法基础上结合模糊逻辑方法发展了基于专家知识的模糊证据权模型；张生元等［19］将模糊证据权方法进一步扩展，发展了双重模糊证据权方法；Coolbaugh等［20］发展了基于地质勘探程度模型的证据权方法；张生元［21］等在双重模糊证据权和基于勘探程度模型的基础上发展了综合证据权方法；成秋明［22］提出了奇异性证据权方法，并给出证据权校正模型；张生元等［23］发展了加权证据权方法和逐步证据权方法；Deng［24］提出了校正证据权模型；Agterberg［3］结合空间加权逻辑回归发展了改进证据权模型；张道军等［25］比较了多种加权证据权模型对证据图层条件独立性克服程度以及实际应用效果；成秋明［26－27］对条件独立性问题采取了完全不同的解决方案，提出了增强证据权模型。除了矿产资源定量评价［28－32］，证据权法在滑坡敏感性评价［33－36］和生态环境［37－40］等多个领域也得到了应用。

当前有很多专业GIS软件包含证据权建模工具，亦有一些地学工作者在商业GIS平台上开发证据权模块。它们有的基于栅格数据［21，28，41－42］，有的则基于矢量数据并通过划分规则格网建立预测单元［32，43－47］。这2种做法的共同之处是预测单元为规则的正方形，虽然栅格（规则格网）数据结构简单、易于计算机处理和实现，但存在以下不足：1）单个栅格（格网）预测单元没有明确的地质含义；2）预测单元大小的确定受主观影响，且不可避免地会出现边界误差；3）先验概率及证据权重的计算基于预测单元，而预测单元采用统一的格网大小，严格来说格网值（有或无矿）反映的是其几何中心的属性，而矿点不可能完全落在格网中心，也就是说该格网单元不能很好地代表落在其内部的矿点，且矿点越分布在预测格网边缘，该问题越严重。为此，笔者提出了采用矢量模型及思想进行模糊证据权建模的方法，以期对解决上述难题有所帮助。

1 基于矢量的证据权方法

1.1 证据权模型

证据权模型的基本原理是把每一种成矿信息看作是二值证据图层，取值为“1”（表示有利成矿，下同）或“0”（表示不利成矿，下同），每个证据图层对成矿预测的贡献就由该证据图层取值状态（“1”或“0”）的权重来确定。证据权重值（即W＋、W－）的计算依赖于二值图层2种取值状态各自对应面积、研究区域总面积以及二值图层中2种取值状态各自包含的矿床面积和整个研究区域的矿床总面积，然后通过贝叶斯公式综合各个证据图层权重，计算得到预测区域的后验概率。这里矿床面积是在假设每个矿点代表一定面域范围的前提下计算得到的。

如图1，对整个研究区来说，先验概率可表示为P（D）＝area（D）/area（A）。其中A表示整个研究区，area（）表示取面积。当考虑证据图层影响时，研究区被分为2个子集合B和B～，它们的后验概率分别为：①P（D｜B）＝area（D∩B）/area（B）＞P（D）；②P（D｜B～）＝area（D∩B～）/area（B）＜P（D）。当引入多个证据图层时，研究区将被分为更多子区域，称为唯一值区域。在普通证据权条件独立性假设前提下，对后验概率进行对数变换可得

对于每个证据图层，有

对照图1，可以很方便地求出W＋、W－的值，其中：

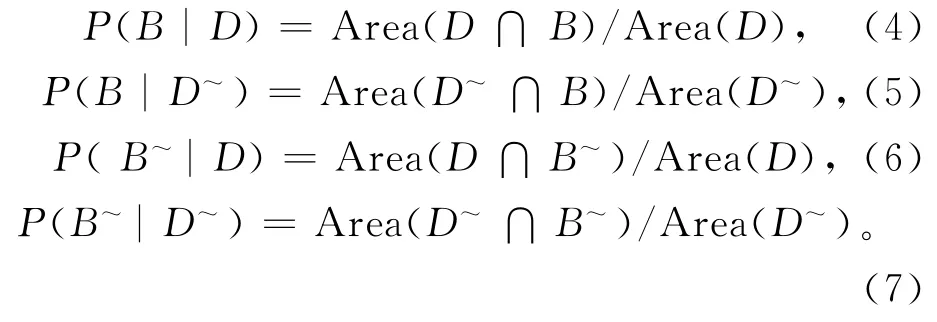
其中：Area（）表示取特定集合的面积，各集合含义见图1。

图1 二值证据图层与预测目标图层关系示意图Fig.1 Relationship between binary evidential layers and the targeting layer

一般有2种方法划分证据图层属性值取值“1”或“0”：一是根据知识或经验划分，二是采用统计方法。后者是通过引入对比值C（contrast）＝W＋－W－，当C取最大值时作为图层二值化的依据，更多时候以标准化C，即作为划分依据［2，12－13］。

1.2 模糊证据权模型

证据图层二值化过程中一个不容忽视的问题是信息丢失，特别是在处理大量地球物理、地球化学和遥感数据等连续型数据时更是如此。成秋明和Agterberg［16］提出使用多值图层代替传统的二值或三值图层，有效解决了信息丢失问题。

模糊证据权模型在实现过程中与普通证据权模型最大的区别在于计算每个证据图层的权重，其他步骤类似。模糊证据权首先计算出“最有利”（仍然表示为“1”）单元集合和“最不利”（仍然表示为“0”）单元集合各自的权重，在此基础上通过模糊隶属度计算介于二者之间的子集合权重［16］。

成秋明等［16］给出了如下公式用于计算模糊权重：

其中，隶属度函数为

当满足B1（x）与B2（y）关于D条件独立时，有

其中：B1和B2表示2个证据图层；B1（x）与B2（y）表示这些图层对应的不同属性取值状态。因为B1（x）和B2（y）对应更小的子集，式（10）只需要在更小的范围内满足条件独立性即成立；它所需要满足的条件独立性比普通证据权所满足的弱条件独立性还要弱，这也从另一方面证明模糊证据权模型降低了后验概率总体上的不确定性。此外，从后验概率方差角度，也可证明在大部分情况下模糊证据权降低了后验概率的不确定性［16］。

1.3 基于矢量的模糊证据权建模过程

基于矢量的模糊证据权应用流程如图2所示。

图2 基于矢量证据权模型流程图Fig.2 Flow chart for the modeling of vector－based WofE

1）对每个证据图层进行数据预处理。对于连续型数据进行离散化，形成多值的分级数据。统一数据格式为矢量的多边形数据。

2）依次叠加证据图层，形成综合证据图层。综合图层由许多多边形混合对象构成，混合对象的属性由叠加前的n个图层共同决定，即混合对象拥有n组属性，分别反映了n类地学要素，因此矢量模型在处理矿产资源评价时可称之为基于不规则地质单元法模型［48］，在只考虑这n个要素时，它是性质均一的。

3）确定有矿地质单元。由于已知矿点是点数据，点没有面积，无法计算空间分布频率，需要将其转化成面数据：以每个矿点为中心，生成半径为固定值的圆，落在圆内的地质单元或地质单元的部分作为有矿单元，最终得到的成矿单元是规则的圆；也可以先把有矿点落入的地质单元作为有矿单元，在此基础上结合空间邻近及语义邻近进行扩展，把扩展后的区域也作为有矿单元。考虑到与基于栅格的证据权模型进行对比，两者的先验概率最好尽可能相等，因此本文采取前一种策略。

4）计算每个证据图层权重。将综合证据图层与矿点缓冲图层进行叠加，形成综合图层，导出其属性，即可计算每个证据图层的证据权重，包括“最有利于成矿”、“最不利于成矿”子集合的确定，它们各自的权重，以及处于“中间状态”子集合隶属度和权重计算。

5）在先验概率基础上，进行证据权重综合及后验概率计算，进而进行靶区圈定。数据处理过程中的各参数计算同上文公式。

需要注意的是，在不确定性计算方面略有差别：令研究区总面积为A，已知矿点数为N，有矿区域面积（即所有矿点代表面积总和）为Area（D），平均矿点代表面积d＝Area（D）/N，研究区总评价单元数可表示为n＝A/d。对于任意证据图层j，Bj和B～j分别表示“有利成矿”和“不利成矿”子集合面积，则有

式中：S2（）表示方差。进而得到对比度C的标准差：

以及标准化C：

式（11）、（12）的右边分别有两项相加组成，后一项相比前一项一般很小，可以忽略不计，前一项的分母关于D互为补集，在D确定的情况下，单独考虑“有利成矿”或“不利成矿”的最优化，都会造成其对立面的非最优化；因而在证据图层二值化的时候，要考察C和t，即式（13）和（14）。而在模糊证据权下，由于隶属度的引入，对于“最有利成矿”子集合，其隶属度为“1”，可以只考虑W＋的最优化；同理，对于“最不利成矿”子集合，可以只考虑W－的最优化。有关隶属度为“1”和“0”的具体划分方法详见下节“数据处理”部分。

2 数据处理

使用文献［22］的实例数据，用本文方法圈定金矿远景靶区。研究区有已知金矿点20处，根据前人研究成果并结合该区具体情况，选取4个证据图层：背斜轴缓冲区、有利岩性接触面缓冲区、化探元素第1主成分经S－A滤波后的结果图层以及化探元素第2主成分经S－A滤波后的结果图层。具体提取过程如下：

背斜轴缓冲区：缓冲区间距为0.5km，共设置20个缓冲带，剩余部分统一赋值为2km（图3）。

图3 背斜轴缓冲区与已知金矿点Fig.3 Spatial relationship between buffer of anticline and the known gold deposits

Goldenville组地层和Halifax组地层的接触线缓冲区：缓冲区间距为0.5km，缓冲带个数为20，剩余部分统一赋值为2km。

组合异常：采用主成分分析方法提取与金矿成矿相关元素的有效组合信息，选取第1主成分和第2主成分，通过S－A滤波分解，分别得到组合异常信息（详见文献［22］）。

由于矿点是点状地物，没有面积，也就无法计算空间分布概率，需要转化为面。以矿点为圆心，0.57 km为半径，生成圆形区域，以此区域代表矿点，这样就可以计算出研究区内有矿单元面积为20.409 3 km2，而研究区面积为7 696.313 1km2，进而得到先验概率为0.002 7。本研究的空间分析部分在ArcGIS软件中进行，属性数据分析借助于ExcelVBA工具和Access数据库，最后再连接回ArcGIS中，做进一步可视化分析和成图工作。

1）证据图层权重计算及模糊化。以背斜轴缓冲区图层为例，如表1所示。首先确定“最有利成矿”子集合，在缓冲距离为1.5km以内时，正权重（W＋）达到最大值，其对应标准化值为2.90，一般认为标准化值大于1.96（对应显著性水平a＝0.05）统计结果是显著的；因此，该值可以作为“最有利成矿”子集合的阈值。再看“最不利成矿”子集合，负权重（W－）的最小值为－3.38，但是其标准化值的绝对值1.57小于1.96，转而寻找次小值为－2.27，其标准化值的绝对值2.27满足0.05的显著性水平，而其对应缓冲距离为5.5km；因此，将缓冲距离5.5 km及以上作为“最不利成矿”子集合。从而确定隶属度为“1”和“0”的子集合所对应权重分别为0.92和－2.27，然后根据式（9）和（10）计算介于二者之间的子集合隶属度及模糊权重。

2）证据图层综合与制图。经过证据图层叠加后，生成的不规则地质单元共26 823个，分为3 660类。计算出每个证据图层不同子集合的证据权重后，即可利用式（10）对4个证据图层进行综合，进而计算后验概率。由于证据权方法的基本假设是各证据图层间满足条件独立性，而在实际应用中这一假设很难得到满足，从而造成后验概率的偏差。成秋明［22］给出了一种解决方案：将后验概率由高到低进行排序和分组，统计不同分组所对应的计算后验概率和观察后验概率，并进行函数拟合，进而对计算后验概率进行校正，在ArcGIS中对校正后验概率大小进行颜色拉伸渲染（图4a）。根据成秋明的研究［22］，后验概率可以看作是多重Cascade过程产生的结果，因而服从多重分形分布，以C－A模型确定后验概率分类，概率阈值0.016 6和0.001 9的两边分别对应不同的直线拟合斜率，从而圈定两级找矿远景区，面积分别占总研究区的6.56%和12.63%（图4b）。可以看到，大部分已知矿点落在后验概率高的区域，那些高后验概率而目前尚未发现矿床的区域应该成为下一步找矿的优先考虑对象。

表1 背斜轴缓冲区图层子集合划分及模糊证据权确定Table 1 Subsets dividing and fuzzy weights determining for the evidential layer of anticline－axes buffering

3 对比研究

采用同样的证据图层和训练样本数据，在GeoDAS软件中进行了基于栅格的试验。为了与矢量模型进行比较，预测网格大小设置为1km×1km，即矿点代表面积为1km2，其先验概率为0.002 6，与矢量模型下的先验概率0.002 7非常接近。4个证据图层分辨率均为0.2km×0.2km，得到后验概率图（图5a）。按相同的方法用栅格证据权圈得远景靶区（图5b）。从后验概率分布的整体形态上看，图5a和图4a基本一致；从靶区范围看，图5b和图4b除局部界线不一致，整体上仍然接近，但图4b在数处已知矿点吻合方面优于图5b（图4b黑圈处）。

通过比较2种数据格式各自模糊权重的计算过程，发现栅格模型在计算面积时存在小于±1%的误差（表2）；从4个证据图层的栅格误差统计结果（图6）可以看出，随着面积减小，整体误差增大，且误差的波动也越大，这反映了栅格模型在面积误差方面具有随机性（相同面积情况下）和趋势性（随面积增大误差变小）。对原始分辨率为0.3km×0.3km的栅格数据进行分析，出现更大误差（表2），21个分组中，14个面积误差超过±3%，6个超过±5%，等级为“2”的组面积误差达到了76.36%。增大的误差来源于“套合”，因为预测网格边长（1.0km）不是栅格分辨率（0.3km）的整数倍；因此，建议栅格模型的预测格网大小最好取原始栅格分辨率的整数倍。矿点数计算方面误差更大（表3），这是因为基于栅格方法的预测格网一般是正方形，而已知矿点不可能刚好落在正方形中心，有的甚至落在边缘，从而导致有矿单元不能很好地代表已知矿点。图7a中，黑色圆点为已知矿点，矩形表示基于栅格证据权模型的有矿单元，该有矿单元代表性较差；而在图7b中，缓冲圆更好地代表了处于圆心处的矿点，这样能最大程度地减小矿点计算误差。表3列举了采用矢量和栅格2种不同方法计算得到的矿点数，有7组误差超过5%。图8为4个证据图层的矿点计算误差统计结果。可以发现，这种误差的分布与该组矿点数之间没有表现出明显的规律性，应该对应于栅格模式下矿点在预测单元内部的随机分布性。因此目前基于栅格的预测单元划分方法所造成的矿点面积计算误差不可避免且具有随机性。

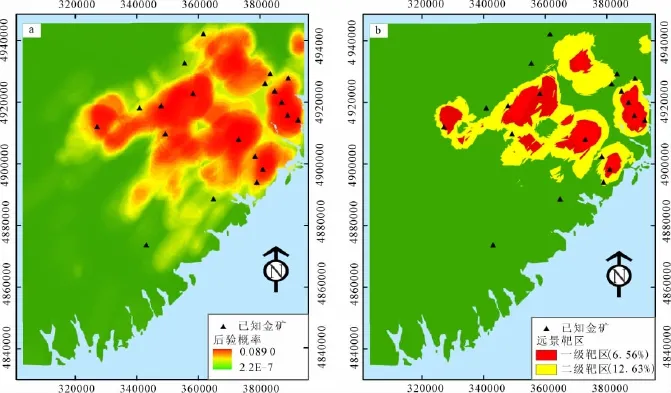
图4 基于矢量的后验概率分布图（a）和远景靶区图（b）Fig.4 Posterior probability map（a）and delineated target（b）for further mineral exploration by vector－based WofE

图5 基于栅格的后验概率分布图（a）和远景靶区图（b）Fig.5 Posterior probability map（a）and delineated target（b）for further mineral exploration by grid－based WofE

图6 基于栅格模型证据权方法单元划分误差分布Fig.6 Distribution of area error from grid－based WofE

这种误差在栅格模式下也是可以控制的：方案一是以矿点为中心扩展一个与预测单元大小相同的正方形区域，设之为A，则A最多可与周围4个预测单元（可用Bi表示，i＝1～4）相交，相交部分的栅格数（或面积）表示为 Area（Bi），可将 Area（Bi）/Area（A）作为第i个预测单元的矿点数；方案二，采用本文基于矢量方法的思路，使用不规则预测单元划分方法代替目前的规则预测单元划分方法，则在忽略原始栅格误差前提下，其结果也将与基于矢量方法一致。

4 结束语

证据权模型是矿产资源定量预测与评价的重要方法，目前证据权建模多是基于栅格实现的，其优点在于表达直观，运算速度快，易于编程实现，但也存在一些不足。本文采用矢量模型代替规则格网划分方法，具有如下优点：1）用具有明确地质含义的地质单元代替规则的网格单元，消除了边界误差，结果便于地质分析、解释；2）以矿点缓冲区作为训练集，可提高矿床（点）代表性，进一步提高预测精度。本文也给出了在格网模式下提高矿点代表性的解决方案，在此基础上矢量和栅格2种建模方式的结果将非常接近，因此使用者可以根据实际情况灵活选用数据格式建立证据权模型。

表2 栅格数据下预测单元面积计算误差Table 2 Calculating errors of prediction unit

表3 栅格数据下矿点数计算误差（栅格）Table 3 Calculating errors of ore occurrences for 200km×200km grid cell

图7 栅格证据权模型（a）和矢量证据权模型（b）有矿单元示意图Fig.7 Schematic diagrams of mine unit for vector－based WofE（a）and grid－based WofE（b）respectively

图8 基于栅格模型证据权方法矿点面积计算误差分布Fig.8 Distribution of ore occurrences error from grid－based WofE

（References）：

［1］Cargill S M，Clark A L.Report on the Activity of IGCP Project 98［J］.Mathematical Geology，1978，10（5）：411－417.

［2］Bonham－Carter G F，Agterberg F P，Wright D F.Weights of Evidence Modelling：A New Approach to Mapping Mineral Potential［C］//Bonham－Carter G F，Agterberg F P.Statistical Applications in the Earthsciences.Ottawa： Geological Survey of Canada，1989：171－183.

［3］Agterberg F P.A Modified Weights－of－Evidence Method for Regional Mineral Resource Estimation［J］.Natural Resources Research，2011，20（2）：95－101.

［4］Singer D A，Kouda R.Application of a Feedforward Neural Network in the Search for Kuruko Deposits in the Hokuroku District，Japan［J］.Mathematical Geology，1996，28（8）：1017－1023.

［5］Brown W M，Gedeon T D，Groves D I，et al.Artificial Neural Networks：A New Method for Mineral Prospectivity Mapping［J］.Australian Journal of Earth Sciences，2000，47（4）：757－770

［6］Oh H J，Lee S.Application of Artificial Neural Network for Gold－Silver Deposits Potential Mapping：A Case Study of Korea［J］.Natural Resources Research，2010，19（2）：103－124.

［7］Porwal A，Carranza E，Hale M.A Hybrid Fuzzy Weights－of－Evidence Model for Mineral Potential Mapping［J］.Natural Resources Research，2006，15（1）：1－14.

［8］Zuo Renguang，Carranza E J M.Support Vector Machine：A Tool for Mapping Mineral Prospectivity［J］.Computers ＆ Geosciences，2009，37（12）：1967－1975.

［9］Bonham－Carter G F.Geographic Information Systems for Geoscientists：Modelling with GIS［M］.Oxford：Pergamon Press，1994.

［10］Ahmed O.Practical Application of Fuzzy Logic and Neural Networks to Fractured Reservoir Characterization［J］.Computers ＆ Geosciences，2000，26（18）：953－962.

［11］Moon W M.Integration of Geophysical and Geological Data Using Evidential Belief Function［J］.IEEE Transactions on Geoscience and Remote Sensing，1990，28（4）：711－720.

［12］Agterberg F P.Computer Programs for Mineral Exploration［J］.Science，1989，245：76－81.

［13］Agterberg F P，Bonham－Carter G F，Wright D F.Statistical Pattern Integration for Mineral Exploration［C］//Gaal G，Merriam D F.Computer Applications in Resource Exploration and Assessment for Mineraland Petroleum.Oxford：Pergamon，1990：1－21.

［14］Bonham－Carter G F，Agterberg F P，Wright D F.Integration of Geological Datasets for Gold Exploration in Nova Scotia［J］.Photogrammetric Engineering ＆Remote Sensing，1988，54（11）：1585－1592.

［15］Cheng Q，Agterberg F P，Bonham－Carter G F.Fractal Pattern Integration for Mineral Potential Estimation［J］.Natural Resources Research，1996，5（2）：117－130.

［16］Cheng Q，Agterberg F P.Fuzzy Weights of Evidence Method and Its Application in Mineral Potential Mapping［J］.Natural Resources Research，1999，8（1）：27－35.

［17］Journel A G.Combining Knowledge from Diverse Sources：An Alternative to Traditional Conditional Independence Hypothesis［J］.Mathematical Geosciences，2002，34（5）：573－596.

［18］Krishnan S.The Tau Model for Data Redundancy and Information Combination in Earthsciences：Theory and Application［J］.Mathematical Geosciences，2008，40（6）：705－727.

［19］张生元，武强，成秋明，等.基于模糊预测对象的证据权方法及其在土地沙漠化评价中的应用［J］.地球科学：中国地质大学学报，2006，31（3）：389－393.Zhang Shengyuan，Wu Qiang，Cheng Qiuming，et al.Weights of Evidence Method Based on Fuzzy Training Layer and Its Application in Desertification Assessment［J］.Earth Science：Journal of China University of Geosciences，2006，31（3）：389－393.

［20］Coolbaugh M，Raines G，Zehner R.Assessment of Exploration Bias in Data－Driven Predictive Models and the Estimation of Undiscovered Resources［J］.Natural Resources Research，2007，16（2）：199－207.

［21］Zhang S，Cheng Q，Chen Z.Omnibus Weights of Evidence Method Implemented in GeoDAS GIS for Information Extraction and Integration［J］.Earth Science：Journal of China University of Geosciences，2008，19（4）：404－409.

［22］Cheng Q.Non－Linear Theory and Power－Law Models for Information Integration and Mineral Resources Quantitative Assessments［J］.Mathematical Geosciences，2008，40（5）：503－532.

［23］张生元，成秋明，张素萍，等.加权证据权模型和逐步证据权模型及其在个旧锡铜矿产资源预测中的应用［J］.地球科学：中国地质大学学报，2009，34（2）：281－286.Zhang Shengyuan，Cheng Qiuming，Zhang Suping，et al.Weighted Weights of Evidence and Stepwise Weights of Evidence and Their Application in Sn－Cu Mineral Potential Mapping in Gejiu，Yunnan Province，China［J］.Earth Science：Journal of China University of Geosciences，2009，34（2）：281－286.

［24］Deng M.A Conditional Dependence Adjusted Weights of Evidence Model［J］.Natural Resources Research，2009，18（4）：249－258.

［25］张道军，成秋明，左仁广，等.加权证据权模型的应用与对比［J］.地球科学：中国地质大学学报，2012，37（6）：1160－1168.Zhang Daojun，Cheng Qiuming，Zuo Renguang，et al.Application and Comparation of Weighted Weights of Evidence Models［J］.Earth Science：Journal of China University of Geosciences，2012，37（6）：1160－1168.

［26］Cheng Qiuming.Integration of AdaBoostand Weights of Evidence Model for Mineral Potential Probabilistic Mapping［C］//Session MG3 “Geo－Process Modeling”at IAMG 2011Annual Conference.Salzburg：［s.n.］，2011.

［27］成秋明.增强证据权（BoostWofE）新方法在矿产资源定量评价中的应用［J］.吉林大学学报：地球科学版，2012，42（6）：1976－1984.Cheng Qiuming.Application of a Newly Developed Boost Weights of Evidence Model（BoostWofE）for Mineral Resources Quantitative Assessments［J］.Journal of Jilin University：Earth Science Edition，2012，42（6）：1976－1984.

［28］成秋明，陈志军，Ali Khaled.模糊证据权方法在镇沅（老王寨）地区金矿资源评价中的应用［J］.地球科学：中国地质大学学报，2007，32（2）：175－184.Cheng Qiuming，Chen Zhijun，Ali Khaled.Application of Fuzzy Weights of Evidence Method in Mineral Resource Assessment for Gold in Zhenyuan District，Yunnan Province，China［J］.Earth Science：Journal of China University of Geosciences，2007，32（2）：175－184.

［29］成秋明，赵鹏大，张生元，等.奇异性理论在个旧锡铜矿产资源预测中的应用：综合信息集成与靶区圈定［J］.地球科学：中国地质大学学报，2009，34（2）：243－252.Cheng Qiuming，Zhao Pengda，Zhang Shengyuan，et al.Application of Singularity Theory in Prediction of Tin and Copper Mineral Deposits in Gejiu District，Yunnan，China：Information Integration and Delineation of Mineral Exploration Targets［J］.Earth Science：Journal of China University of Geosciences，2009，34（2）：243－252.

［30］Cassard D，Billa M，Lambert A.Gold Predictivity Mapping in French Guiana Using an Expert Guided Data－Driven Approach Based on a Regional－Scale GIS［J］.Ore Geology Reviews，2008，34（3）：471－500.

［31］Porwal A，González－Álvarez I，Markwitz V，et al.Weights－of－Evidence and Logistic Regression Modeling of Magmatic Nickel Sulfide Prospectivity in the Yilgarn Craton，Western Australia［J］.Ore Geology Reviews，2010，38（3）：184－196.

［32］薛顺荣，肖克炎，丁建华.基于MRAS的证据权重法在香格里拉地区的综合信息成矿预测［J］.吉林大学学报：地球科学版，2008，38（5）：738－744.Xue Shunrong，Xiao Keyan，Ding Jianhua.Multi－Source Information Metallogenic Prognosis with Weighting of Evidence Based on MRAS in Shangri－La［J］.Journal of Jilin University：Earth Science Edition，2008，38（5）：738－744.

［33］Neuhäuser B，Terhorst B.Landslide Susceptibility Assessment Using“Weights－of－Evidence”Applied to a Study Area at the Jurassic Escarpment（SW－Germany）［J］.Geomorphology，2007，86（1/2）：12－24.

［34］王志旺，李端有，王湘桂.证据权法在滑坡危险度区划研究中的应用［J］.岩土工程学报，2007，29（8）：1268－1273.Wang Zhiwang，Li Duanyou，Wang Xianggui.Zonation of Landslide Hazards Based on Weights of Evidence Model［J］.Chinese Journal of Geotechnical Engineering，2007，29（8）：1268－1273.

［35］Regmi N R，Giardino J R，Vitek J D，et al.Modeling Susceptibility to Landslides Using the Weight of Evidence Approach：Western Colorado，USA［J］.Geomorphology，2010，115（1/2）：172－187.

［36］Cervi F，Berti M，Borgatti L，et al.Comparing Predictive Capability of Statistical and Deterministic Methods for Landslide Susceptibility Mapping：A Case Study in the Northern Apennines（Reggio Emilia Province，Italy）［J］.Landslides，2010，7（4）：433－444.

［37］Romero－Calcerrada R，Luque S.Habitat Quality Assessment Using Weights－of－Evidence Based GIS Modelling：The Case of Picoidestridactylus as Species Indicator of the Biodiversity Value of the Finnishforest［J］.Ecological Modelling，2006，196（1/2）：62－76.

［38］Cho S H，Poudyal N C，Roberts R K.Spatial Analysis of the Amenity Value of Green Open Space［J］.Ecological Economics，2008，66（2/3）：403－416.

［39］Romero－Calcerrada R，Barrio－Parra F，Millington J D A，et al.Spatial Modelling of Socioeconomic Data to Understand Patterns of Human－Caused Wildfire Ignition Risk in the SW of Madrid（Central Spain）［J］.Ecological Modelling，2010，221（1）：34－45.

［40］Gorney R M，Ferris D R，Ward A D，et al.Assessing Channel－Forming Characteristics of an Impacted Headwater Stream in OHIO，USA［J］.Ecological Engineering，2011，37（3）：418－430.

［41］Sawatzky D L，Raines G L，Bonham－Carter G F，et al.Spatial Data Modeller（SDM）：ArcMAP 9.3Geoprocessing Tools for Spatial Data Modelling Using Weights of Evidence，Logistic Regression，Fuzzy Logic and Neural Networks［EB/OL］.（2008－11－26）［2012－06－18］.http：//arcscripts.esri.com/details.asp？dbid＝15341.

［42］雷静.地下水环境脆弱性的研究［D］.北京：清华大学，2002.Lei Jing.Study on Groundwater Vulnerability［D］.Beijing：Tsinghua University，2002.

［43］陈永良，刘大有，王全明.基于矢量结构GIS的证据加权模型［J］.地质论评，2000，46（增刊1）：141－145.Chen Yongliang，Liu Dayou， Wang Quanming.Weights of Evidence Modeling Based on Vector－Structure GIS［J］.Geology Review，2000，46（Sup.1）：141－145.

［44］胡光道，陈建国.金属矿产资源评价分析系统设计［J］.地质科技情报，1998，17（1）：45－49.Hu Guangdao，Chen Jianguo.Design of the Metallic Mineral Resources Assessment and Analysis System［J］.Geological Science and Technology Information，1998，17（1）：45－49.

［45］陈永清，夏庆霖，黄静宁，等.“证据权”法在西南“三江”南段矿产资源评价中的应用［J］.中国地质，2007，34（1）：132－141.Chen Yongqing，Xia Qinglin，Huang Jingning，et al.Application of the Weights－of－Evidence Method in Mineral Resource Assessments in the Southern Segment of the“Sanjiang Metallogenic Zone”，Southwestern China［J］.Geology in China，2007，34（1）：132－141.

［46］肖克炎，张晓华，宋国耀，等.应用GIS技术研制矿产资源评价系统［J］.地球科学：中国地质大学学报，1999，24（5）：525－528.Xiao Keyan，Zhang Xiaohua，Song Guoyao，et al.Development of GIS－Based Mineral Resources Assessment System［J］.Earth Science：Journal of China University of Geosciences，1999，24（5）：525－528.

［47］肖克炎，杨东来，严光生，等.矿产资源评价系统（MRAS）的一些改进［J］.矿床地质，2002，21（增刊1）：75－78.Xiao Keyan，Yang Donglai，Yan Guangsheng，et al.Some Improving of Mineral Resource Appraise System（MRAS）［J］.Mineral Deposits，2002，21（Sup.1）：75－78.

［48］成秋明，刘江涛，张生元.GIS中的空间建模器技术及其在全国矿产资源潜力预测中的应用［J］.地球科学：中国地质大学学报，2009，34（2）：338－346.Cheng Qiuming，Liu Jiangtao，Zhang Shengyuan.Application of GIS－Model Builder Technology for National Mineral Resource Assessment［J］.Earth Science：Journal of China University of Geosciences，2009，34（2）：338－346.