裂缝等效介质模型对裂缝结构和充填介质参数的适应性

沈金松，詹林森，马 超

1.中国石油大学地球物理与信息工程学院，北京 102249

2.油气资源与探测国家重点实验室，北京 102249

3.中国石油集团公司物探重点实验室，北京 102249

0 前言

依据地震响应特征识别和描述储层的裂缝分布、孔隙中的流体性质等，已成为裂缝性含油气储层探测和评价的中心议题。地震波动理论［1］、大型物理模拟实验［2］和生产实践［3］均证实：地层中裂缝的规模分布会引起介质中地震波传播的各向异性特征，不同方向上P波、S波和转换波的传播模式和传播速度具有明显的差异；这也为地震勘探实现裂缝分布预测和定量评价提供了物理基础。

然而，限于裂缝各向异性地层地震响应的复杂性，目前对裂缝性地层的研究大多采用各种假设下的等效介质模型或对应的近似解［4－5］。例如，目前应用最广的 Hudson［6－8］裂缝模型是单一方向裂缝平行排列的近似模型，它基于小裂缝密度和小纵横比薄圆片裂缝的假设，导出了裂缝参数与等效弹性参数的一阶和二阶渐近关系。对于大裂缝密度，Hudson的二阶渐近关系中二阶修正项的影响大于一阶修正项的影响，导致二阶渐近关系计算的等效弹性模量与实际介质弹性特性不符。因此，Hudson［8］的二阶渐近关系不适用大裂缝密度介质的评价和描述。Cheng［9］基于Eshelby的长波长静态解析解给出了与Hudson二阶渐近展开相似的展开项，放宽了裂缝小纵横比的限制，解决了Hudson二阶渐近展开在大裂缝密度情况下无法得到有物理意义解的问题。

为了更好地定量考察Hudson［8］裂缝模型的精度和适用范围，笔者在简单回顾裂缝各向异性介质弹性参数关系的基础上，分析了Eshelby理论响应、Hudson裂缝模型和Liu含裂隙介质模型的弹性响应关系；通过与Eshelby模型理论响应的比较，在饱水和干裂缝状态下，考察了Hudson一阶和二阶渐近关系对不同裂缝密度、裂缝孔隙纵横比的适用范围；分析了Cheng［9］等的Pade二阶渐近关系与Hudson模型二阶修正关系在模拟裂缝性地层等效弹性响应特征方面的适应性；对比了Liu含裂隙介质模型和Hudson模型对裂缝密度、裂缝孔隙纵横比的适用范围的差异；指出了Liu含裂隙介质模型中法向柔度和切向柔度对裂缝孔隙结构和其中充填介质的敏感性差异，为裂缝性储层流体识别和定量评价提供了理论基础。

1 各向异性介质中弹性参数与速度的关系

基于线性弹性理论，应力τ和应变ε的9个分量存在如下线性关系［1］：

式中，C为4阶张量的刚度系数阵。

由切应力互等原理知道，应力和应变具有对称性。因此，描述任意各向异性介质最多需要21个弹性刚度分量。C［1］可以退化为

对于横向各向同性（VTI）介质（图1a），地震波的波速只与传播方向有关。根据对称性原理，其弹性刚度系数有C22＝C11，C44＝C55，C23＝C13，C12＝C11－2C66，其他元素均为0，其刚度系数阵［9］退化为

若将VTI介质的对称轴旋转90°，就变为水平对称轴的垂向各向同性（HTI）介质（图1b），其由单组平行于垂直裂缝的各向同性介质构成，相应的弹性刚度阵［9］为

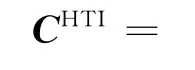
当S波垂直入射到HTI介质时，会产生快S波和慢S波，发生横波分裂。快S波的偏振方向平行于裂缝平面，慢S波的偏振方向垂直于裂缝平面。

由关系式（3）可知：对于横向各向同性介质，仅需要5个独立弹性参数（C11，C13，C33，C44，C66）即可描述其弹性性质；相应的四阶弹性张量中的参数为C1111，C1133，C3333，C2323和C1212，其他分量为0。

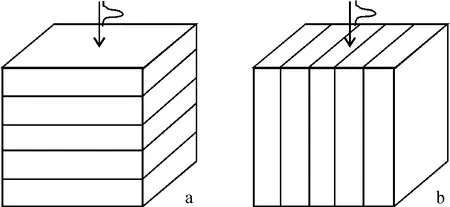
图1 VTI（a）和 HTI（b）介质示意图Fig.1 Illustration of VTI（a）and HTI（b）medium

根据各向异性介质中的弹性本构方程，得到介质中准纵波和两类准横波的相速度［10］：

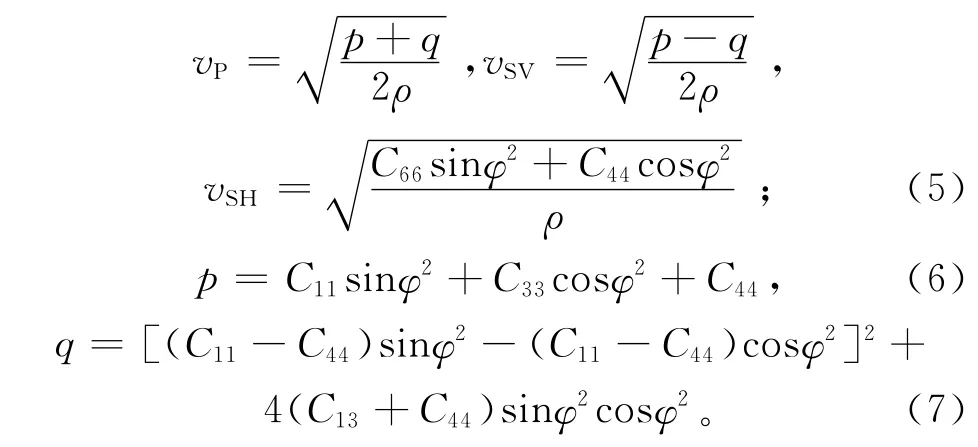
式中：ρ为裂缝介质的等效密度；φ为入射角，即入射波与裂缝介质对称轴的夹角。

对于介质中的垂直裂缝，笔者均采用水平对称轴的HTI介质模拟。对于实际地层模型的裂缝分布，用不同纵横比的椭球近似薄硬币形或圆片形裂缝嵌入各向同性基质形成裂缝性介质模型，再用等效介质模型计算近似的等效刚度张量C，进而模拟研究各向异性速度随入射角和裂缝密度变化的响应规律。

2 基于等效介质理论的裂缝模型及数学表达

2.1 Eshelby模型的弹性系数关系

1957年Eshelby［11］应用常应力和应变得到了椭球形包裹体嵌入各向同性基质中形成的混合介质内部应变的解析解。考虑混合介质内整个体积域V的位能最小，可以得到等效弹性模量。若混合介质的均匀应变为εA，则混合介质的等效弹性张量C＊满足如下关系：

式中，Eint是由于裂缝存在而产生的能量变化，且为包裹体的自由应变，通过包裹体的体积方程和纵横比组成的矩阵与实际应变联系起来，且有

其中：Φ为孔隙度为无裂缝均匀介质的弹性系数为应变对应的一阶近似弹性系数，由Cheng［9］导出（附录 A）。

2.2 Hudson模型的渐近展开式

Hudson模型［6－7］的假设为：1）裂缝存在于均匀各向同性介质中，且裂缝中的介质可看成基质中的包裹体，能适用Eshellby的经典包裹体理论；2）地震波长范围内裂缝均匀且呈不连续稀疏分布，裂缝可用小纵横比的扁椭球体近似且其体积占介质整体的比例很小，即裂缝孔隙度很小；3）介质中包含的定向排列裂缝比地震波长小得多，可用长波长近似导出裂缝各向异性介质的近似表达式。

基于上述假设，Hudson［6－7］运用散射理论分析了包含薄币型椭球体裂缝的弹性固体介质的平均波场，将含裂缝介质的弹性系数等效为各向同性介质中的弹性系数及裂缝存在而产生的一阶和二阶扰动量之和。该理论将裂缝的微观结构参数，包括裂缝的半径、密度及纵横比等参数，与裂缝介质的宏观弹性性质相联系，为裂缝介质的定量评价奠定了理论基础。若介质中只有一组平行排列且均匀分布的薄圆币型裂缝，且裂缝的尺度和分布间距都远小于波长，对于裂缝面法线方向为水平的垂直裂缝，裂缝介质中平均波场的等效刚度模量为

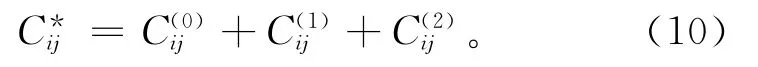
式中：为无裂缝均匀介质的弹性系数为一阶校正量，即单个裂缝独立作用时对弹性参数影响的修正项为二阶校正量，表示不同裂缝间耦合作用对弹性参数影响的修正项。

一阶和二阶修正量具有如下关系：

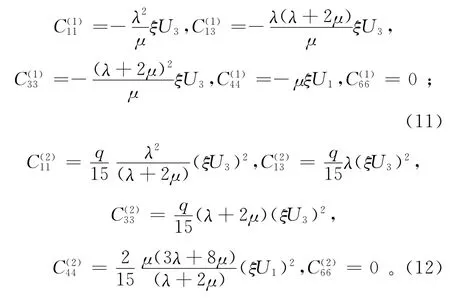
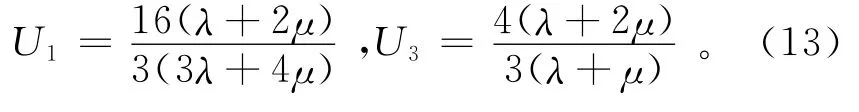
需要注意的是，上述近似关系的导出假设了裂缝密度不受张开度影响，且一阶、二阶校正量遵守TI介质的对称关系。裂缝中的填充物为“弱”的标准取决于填充物的形状、纵横比及填充物和基质模量的相对比值。干裂缝的填充物模量可设为0，饱含流体的裂缝其填充物的剪切模量为0。对于Hudson的大纵横比裂缝和多组裂缝排列时裂缝介质等效弹性的计算关系见文献［6－7］。

2.3 Liu含裂隙介质模型的近似关系

刘恩儒等［12］在Hudson模型假设的基础上，提出了计算裂缝柔度系数Z的模型［13］，导出了裂隙介质弹性本构关系式。利用该弹性本构关系，可将几种常用的裂缝模型（如孤立滑移面裂缝模型、非连续接触裂缝模型、液体薄层裂缝模型等）用统一的弹性关系表示，且当已知裂缝表面的一些信息时，可将宏观测得的柔度系数直接与裂隙的微观结构参数联系起来。

对于平行裂缝的情况，设体积为V的含流体介质中包含Nf个表面积为Sr的裂缝，其弹性介质的平均应变ε可表示为

式中：σ是基质的平均应变张量；s（0）是基质的柔度张量；s（1）是由裂缝的存在而引起的柔度张量扰动量。则等效介质的应变表达式为

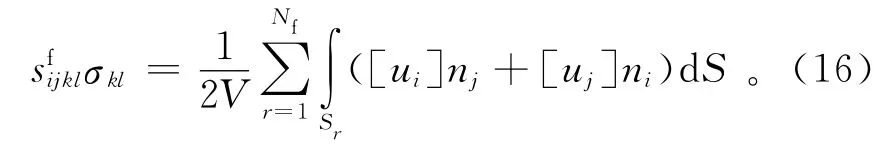
式中：sf表示由于裂缝存在而引起的额外柔度张量；［ui］是与Sr相关的滑动位移的第i个分量；ni为第i个裂缝面法向分量，当所有的裂缝都定向排列时，其法向为n。可以将V内每一个裂缝替换成平均裂缝，表面积为S，其线性滑动边界条件为［13］

式中：t为裂缝面上的张力是裂缝平面的平均滑动位移量；为了与不考虑线性滑移效应的裂缝柔度矩阵s相区别，遵照文献中的惯用符号，在线性滑动模型中换用｛Z｝表示与裂缝的内部充填物和互连情况相关的柔度矩阵。

根据Liu等［13］的简单无约束裂缝模型导出的结果，等效介质的应变表达式可写为

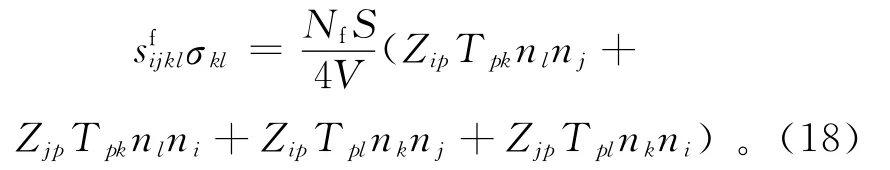
式中：｛T｝为介质中一点的应力，取决于｛Z｝。由于裂缝的存在而引起的柔度扰动量为

(2)地下水的径流。地表水通过岩体风化网状裂隙及节理裂隙缓慢下渗，并逐步汇聚到F1、F2断裂带中，再沿F1、F2断裂带渗流，并以地下水为载体，在长距离的运移过程中吸收周围岩石骨架中的热能及矿物质，形成载热流体赋存于F1、F2断裂带中。F2断裂在深部被F1所阻后，地热水沿F1断裂带上涌，在地势低洼处排泄形成温泉。

其中，Df＝（NfS）/V。

若统计意义上裂缝法向均为n，则只需用切向和法向柔度ZT和ZN即可表示裂缝的弹性参数：

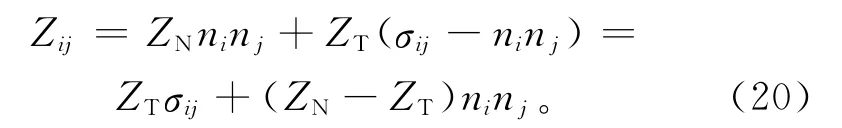
式（19）可改写为

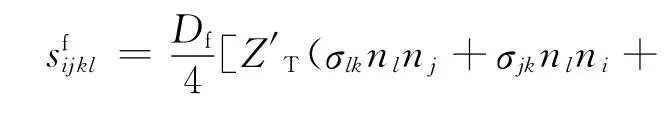
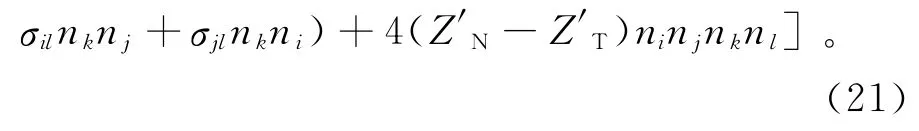
其中：Z′N＝ZNTN；Z′T＝ZTTT。将四阶张量简化为二阶张量，则sijkl＝spq。对柔度矩阵s求逆即可得到等效弹性常量或刚度矩阵C［16］。其中与裂缝相关的参数为Z′N和Z′T。

下边以Hudson裂缝模型［8］为例，考虑不同裂缝接触情况下柔度系数的具体表达式。对于孤立滑移面裂隙模型，裂缝被模拟成为平均半径为ac的孤立圆形域，均匀分布于介质中，则切向和法向柔度ZT和ZN与裂缝参数的关系为

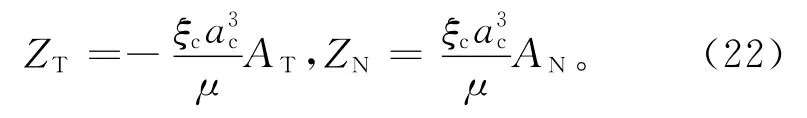
式中：ξc为单位区域内的裂缝数，即裂缝面密度；AN和AT与裂缝结构参数关系如下：

3 Eshelby模型和Hudson模型响应特征的数值模拟

3.1 Hudson一阶、二阶近似和Eshelby静态解的对比

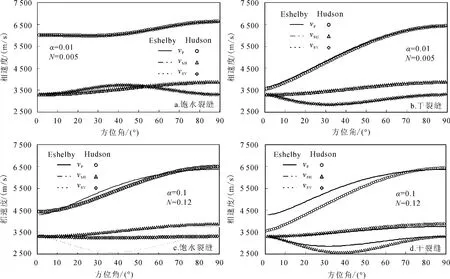
图2 Hudson二阶模型和一阶模型qP、qSV、qSH波随入射角的变化Fig.2 Comparison of the phase velocities of qP，qSV，qSH wave based on the Eshelby analytic expression and Hudson first order approximation

基于Eshelby长波长近似理论和椭球包裹体模型导出的解析解适用的裂缝密度极限约为0.24［11］，适用的椭球体长短轴比（纵横比）理论上为0→∞，Hudson模型适用的裂缝密度范围随其修正阶数的提高而增大，其一阶修正项适应的裂缝概率密度约为0.1，二阶修正项适应的裂缝密度范围相对增大。图2给出了Eshelby模型和Hudson一阶修正项模型计算的准纵波（qP）、准横波（qSV、qSH）波速随入射角的变化关系。基质为泊松体，拉梅常数均取39 GPa，裂缝饱水时的体积模量为2.25GPa。从图2a，b可以看到，探讨弱填充物情况下，Hudson一阶修正［6］和Eshelby模型［11］的结果完全吻合。因此，对于裂缝纵横比小于等于0.01的情况，Hudson模型的一阶近似即能适用于裂缝性地层的等效参数计算。由于对比结果与图2a，b相似，限于篇幅，纵横比为0.01～0.10的对比结果在此没有给出。对于大纵横比的情况，从图2c，d可以看出，纵横比为0.1时，两模型的模拟结果出现差异。这说明Hudson一阶近似只适用于纵横比小于0.1的小纵横比裂缝介质；大纵横比时，需要考虑裂缝之间散射耦合的影响。

图3比较了饱含水和干裂缝岩石情况下，一阶、二阶Hudson修正模型即计算的纵横波速度。对于Hudson二阶近似［8］的情况，从图中结果看到，尽管二阶项的校正效应对于含水情况下影响有限，但是对于干裂缝影响很显著，尤其是qSH波。

为了理解Hudson模型一阶和二阶修正项的相互影响，下边定量分析2个修正项与微观裂缝参数的关系。Hudson模型只能在小裂缝密度下才能收敛，其数学含义是Hudson模型［8］的二阶项相对于一阶项在小裂缝密度时渐近于0。以基质为泊松体的干裂缝为例进行分析。对于基质为泊松体的干裂缝，λ＝μ，U3＝2，U1＝16/7，q＝58，则 Hudson模型的一阶和二阶项为相应的等效介质的弹性刚度系数为

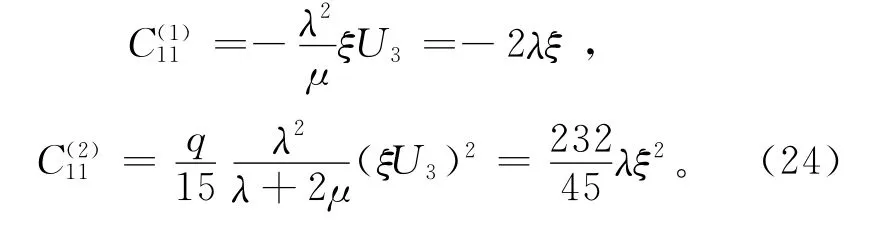
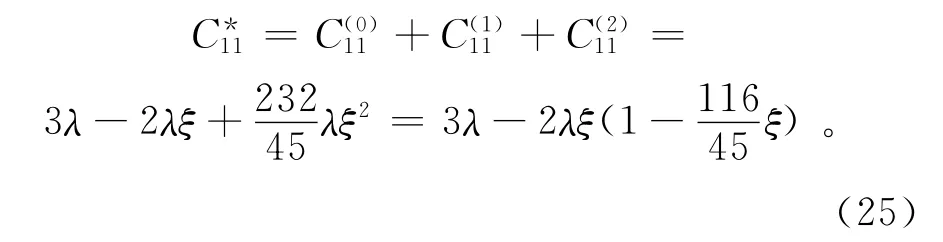
由式（25）知道，当ξ＝45/116≈0.39时，Hudson模型的二阶修正项与一阶项抵消了。更严重的是，等效介质的弹性刚度系数在某特定裂缝密度ξ＝45/232≈0.19时存在一个拐点，此后等效模量随裂缝密度的减小而增大，这与事实不符。

图4是干裂缝情况下，Hudson模型的一阶和二阶修正项对应的刚度模量随裂缝密度变化，等效刚度模量用与背景介质的弹性模量比值表示。从图4中看到：裂缝密度为0.1以内时，一阶修正项和二阶修正项的模拟结果基本接近；随着裂缝密度增大，刚度模量比值的差异增大；对应于二阶修正项，裂缝密度大于0.19时，刚度模量比值在出现极小值后单调增大，与实际介质的响应特征不符。因此，干裂缝介质中，在裂缝密度小于0.19的条件下，Hudson二阶近似是有效的。

3.2 Hudson模型和Cheng的Pade近似解的对比

为了克服Hudson二阶修正项在裂缝密度大于0.19之后的物理不可实现响应特征，Cheng等［9］使用Pade近似给出了一个新的二阶修正模型：

对Eshelby的解析解有如下Pade近似［9］：

对比式（26）和式（27），得到如下Pade近似修正项的系数：

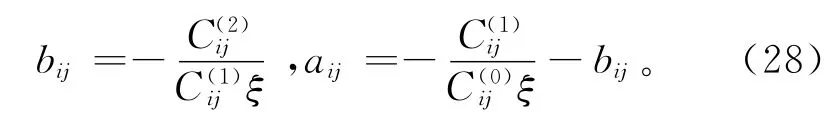
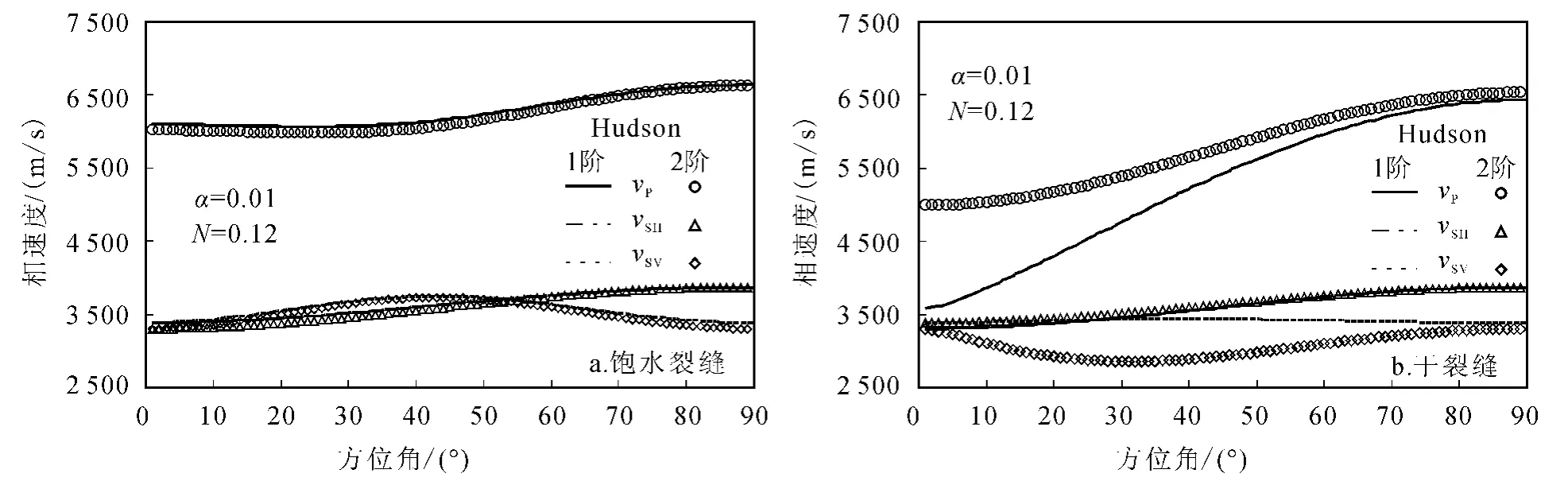
图3 Hudson二阶模型和一阶模型qP、qSV、qSH波随入射角的变化Fig.3 Comparison of the phase velocities of qP，qSV，qSH wave based on the Hudson first and second order approximations

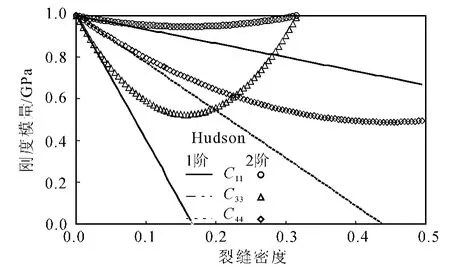
图4 干裂缝介质中Hudson一阶和二阶模型计算的弹性波标准化刚度模量随裂缝密度的变化Fig.4 Comparison of the elastic stiffness of the wave propagated in medium with dry fracture based on the Hudson first and second order approximations，fracture aspect is 0.01

图5是干裂缝和饱水裂缝情况下Hudson二阶修正和Pade近似的标准化刚度系数C11、C33和C44随裂缝密度的变化情况。对比图5可知，对于干裂缝的情况，基质的刚度模量和含裂缝介质的刚度模量的对比度更大。因此，用干裂缝的模型讨论Pade近似对大裂缝密度和纵横比的适应性更具实用意义。模拟结果看到，Pade近似在0.2以上的大裂缝密度情况下，依然可得到收敛结果。

3.3 Hudson模型刚度模量对裂缝孔隙结构（纵横比）的响应

从上面的分析可见，无论是纵横波速度还是刚度张量都与裂缝的含流体情况、裂缝密度相关，除此之外，还与裂缝孔隙形状有关。从图6的饱水裂缝模拟结果可见：纵横比越小，Hudson二阶近似［8］越容易收敛，且发散对应的拐点裂缝密度越大；裂缝张开度为0.1时，拐点最小，此时的裂缝密度为0.19左右。对于实际的裂缝介质，裂缝密度一般不超过0.40，纵横比大多小于0.02；因此，对于 Hudson二阶近似几乎都能使用。

4 Liu含裂隙介质模型和Hudson模型适用性对比分析

4.1 Liu含裂隙介质模型和Hudson模型的对比分析

考虑到Eshelby理论的解析解对裂缝包裹体作了椭球形近似且忽略了裂缝之间的耦合作用。从20世纪60年代开始，人们一直探索研究能够实用的等效介质模型，提出了Hudson模型等［10］。对于Hudson模型，其小裂缝密度和小纵横比假设限制了它的适用性，前述模拟结果知道，对于干裂缝介质，Hudson模型适用的裂缝密度为0.2以下，裂缝纵横比低于0.02。Pade近似［9］使裂缝密度和纵横比限制范围放宽到0.3左右。

鉴于 Hudson模型上述问题，Liu等［12－13，15－16］直接应用Hudson等的假设条件，基于裂隙柔度系数Z导出了裂隙介质中弹性本构关系式，而后，利用该关系将孤立滑移面裂隙模型、非连续接触裂纹的裂隙模型和液体薄层裂隙模型等用一个统一关系表示。该模型的特点是当已知裂隙表面的一些信息时，可以将宏观的柔度系数直接与裂隙的微观结构信息联系起来，即将裂隙的微观参数与介质的弹性常数直接相联系。

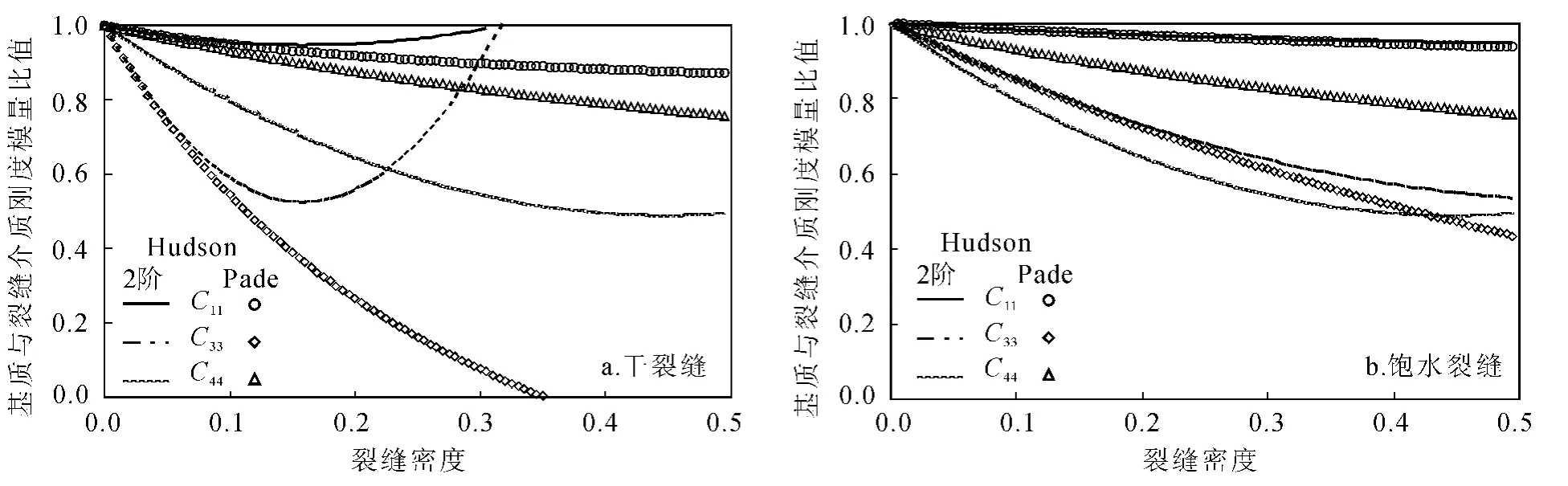
图5 干裂缝和饱水裂缝时Hudson二阶模型和Pade近似随裂缝密度变化的刚度模量响应Fig.5 Comparison of the elastic stiffness of the wave propagated in medium with water saturated and dry fracture based on the Hudson second order and Pade approximation，fracture aspect is 0.01

图6 饱水裂缝介质中Hudson二阶近似时C11随裂缝密度的变化Fig.6 Comparison of the elastic stiffness of the wave propagated in medium with water saturated based on the Hudson second order approximation，fracture aspect is variable

图7显示的是饱气裂缝和孤立分布饱水裂隙情况下，Hudson二阶近似［8］、Pade近似［9］和 Liu含裂隙介质模型［15－16］的标准化刚度模量C11、C66随裂缝密度的变化情况。从图7a中看到，Hudson模型二阶近似最先出现无物理意义的发散结果，而Liu含裂隙介质模型在裂缝密度达0.35还是收敛的。从图7b中可见：对于C11，Hudson模型近似与Liu含裂隙介质模型的结果基本一致；而对于C66，3个模型的结果与饱气情况总体一致。从图7a，b看到，饱气和饱水2种情况下，对于C66曲线的3个模拟结果在裂缝密度为0.05附近开始出现偏差，Liu模型［15－16］在裂缝密度大于0.28后出现较大偏差，而Hudson模型二阶近似与Pade近似在裂缝密度0.25～0.28时还基本一致，之后Hudson模型二阶近似结果开始发散。因此，综合C11、C66随裂缝密度变化的模拟结果知道，Liu含裂隙介质模型［15－16］考虑了散射体之间的影响，在通常裂缝密度范围内，不出现发散的问题，具有较高的精度。

4.2 Liu含裂隙介质模型对裂缝密度、孔隙结构及流体的敏感性

为了分析Liu含裂隙介质模型对裂缝密度、孔隙结构及流体的敏感性，利用裂缝半径a与单位长度上的裂缝数Hf（线密度）的比值a/Hf，考察Liu含裂隙介质模型的弹性响应特征。图8给出了饱水裂缝介质中Liu含裂隙模型标准化刚度模量C11和C66随裂缝密度a/Hf的变化，裂缝的平均纵横比为0.01。从图8中看到：C11随a/Hf变化幅度极小，可以认为基本不受a/Hf变化的影响；而C66随a/Hf变化幅度较大，尤其在a/Hf为0.01时，即密集分布的小开度裂缝介质中，C66随裂缝密度增大，标准化刚度模量急剧减小。

图9为饱含水情况下，a/Hf取0.01和0.50时，标准化刚度模量C11、C66随裂缝密度和纵横比的变化。从图9中可见：C66标准化刚度模量对a/Hf值比较敏感，但对纵横比不敏感；C11标准化刚度模量对a/Hf值和纵横比极为敏感。在纵横比极小且裂缝密度不大时，裂缝各向异性的影响可以忽略。

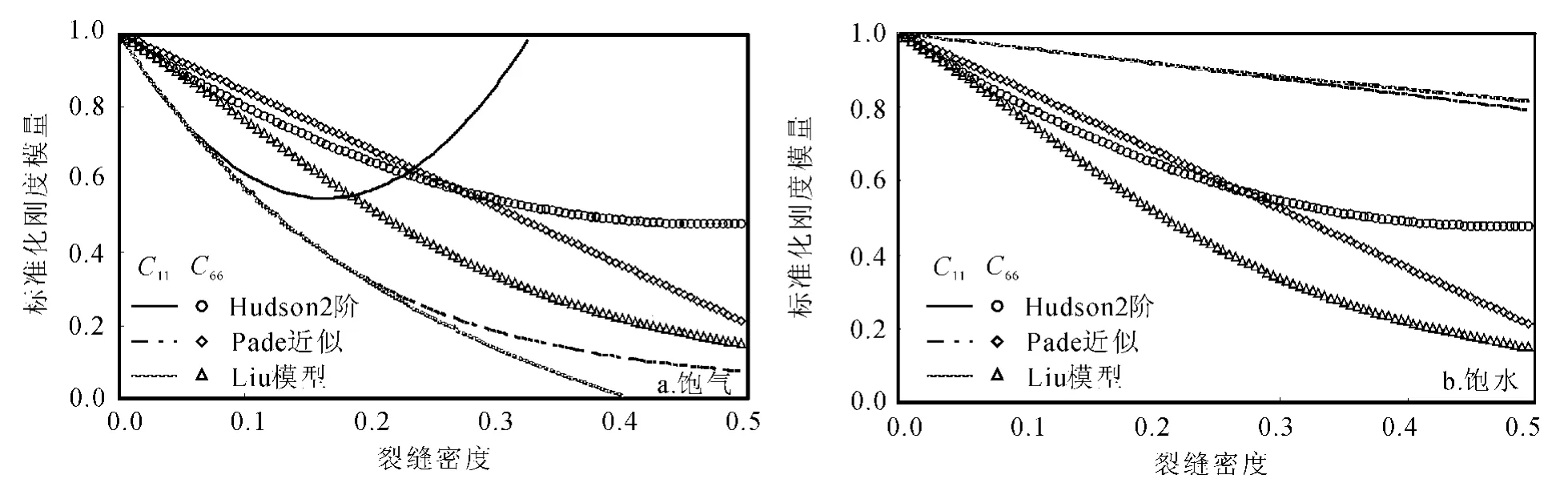
图7 饱气和饱水裂缝时三类等效介质裂缝模型计算的标准化刚度C11、C66随裂缝密度的变化Fig.7 Comparison of the elastic stiffness of the wave propagated in medium with gas saturated and water saturated medium based on the Hudson second order，Liu and Pade approximation，fracture aspect is 0.01

图8 饱水裂缝介质中Liu模型计算的标准化刚度模量随a/Hf的变化Fig.8 Comparison of the elastic stiffness of the wave propagated in medium with water saturated fractures as a function of a/Hfbased on the Liu approximation

图9 饱水裂缝介质中标准化刚度模量C11、C66随裂缝密度和纵横比变化Fig.9 Comparison of the elastic stiffness C11and C66of the wave propagated in medium with water saturated fractures as a function of a/Hfand fracture density based on the Liu approximation

图10是不同纵横比、不同裂缝密度时含裂隙模型（Liu）计算得到的准纵横波速度随方位角的变化情况。由于含气和干裂缝对纵波速度各向异性的影响几乎相同，所以没有显示。图10中对比了饱水和饱气时对纵横波速度的影响，可以看出饱气时对纵波速度各向异性的影响更加明显；而当纵横比和裂缝密度比较小时，两类准横波也有差异。

5 结论

采用数值模拟分析方法，讨论了Hudson模型对裂缝各向异性介质的适用范围，利用Pade近似导出的Hudson模型近似关系，明确了Hudson二阶展开对大裂缝密度的适应性，且可以得到比Hudson模型精度高的结果。由Liu含裂隙介质模型和Hudson模型模拟结果的对比可知，Liu和Hudson二阶近似在裂缝密度小于0.1时精度相近，Liu模型和Pade近似可以在裂缝密度小于等于0.2范围内得到一致的结果。

数值模拟结果对比分析表明，对于小纵横比（小于等于0.01）的情况，Hudson模型和基于Eshelby理论的近似解析解在小裂缝密度的情况下吻合得很好，即Hudson的“弱介质填充物”假设只适应于小纵横比和小裂缝密度的介质。而Liu含裂隙介质模型和Hudson模型的Pade近似可以适用于大纵横比和较大裂缝密度的情况。模拟结果还显示，干裂缝时，纵横比对标准化刚度模量的影响极小，而饱含水时，纵横比对标准化刚度模量的影响显著；这为裂缝性储层中流体判识和定量评价提供了物质基础。另外，标准化刚度模量依赖于a/Hf变化，a/Hf值越小，刚度模量衰减越快；这也是利用弹性参数定量评价裂缝参数的物理基础。Liu模型的模拟结果表明，在裂缝饱含水时，准纵波速度对裂缝各向异性敏感，当裂缝孔隙纵横比和裂缝密度均较小时，准横波速度对饱水裂缝各向异性表现一定敏感性。

图10 Liu模型饱水和饱气介质纵横波相速度随方位角的变化Fig.10 Comparison of the phase velocities of the compressive and shear waves propagated in medium with water and gas saturated fractures based on the Liu approximation

（References）：

［1］Biot M A.Theory of Propagation of Elastic Waves in a Fluid Saturated Porous Solid：I： Low－Frequency Range［J］.J Acoustic Soc Ame，1956，28（2）：168－178.

［2］魏建新，狄帮让.裂隙张开度对地震波特性影响的模型研究［J］.中国科学：D辑：地球科学，2008，38（增刊I）：211－218.Wei Jianxin，Di Bangrang.The Model Study of the Influence on the Characteristics of Seismic Waves by Fracture Apertura［J］.Science in China：Series D：Earth Sciences，2008，38（Sup.I）：211－218.

［3］Thomsen L.Weak Elastic Anisotropy［J］.Geophysics，1986，51（10）：1954－1966.

［4］Hashin Z，Shtrikman A.A Variational Approach to the Theory of the Elastic Behavior of Multiphase Materials［J］.Journal of the Mechanics and Physics of Solids，1963，11：127－140.

［5］Kuster G T，Toksoz M N.Velocity and Attenuation of Seismic Waves in Two－Phase Media：Part I：Theoretical Formulation and Part II：Experimental Results［J］.Geophysics，1974，39：587－618.

［6］Hudson J A.Overall Properties of a Cracked Solid：Math Proc［J］.Cambridge Phil Soc，1980，88：371－384.

［7］Hudson J A.Wave Speeds and Attenuation of Elastic Waves in Material Containing Cracks［J］.Geophys J Roy Astr Soc，1981，64：133－150.

［8］Hudson J A.Seismic Wave Propagation Through Material Containing Partially Saturated Cracks［J］.Geophys J Ro Astr Soc，1988，92：33－37.

［9］Cheng C H.Crack Models for a Transversely Anisotropic Medium［J］.Journal of Geophysical Research，1993，98：675－684.

［10］Hudson J A，Liu E，Crampin S.Transmission Properties of a Plane Fault［J］.Geophys J Int，1996，125（2）：559－566.

［11］Eshelby J D.The Determination of the Elastic Field of an Ellipsoidal Inclusion，and Related Problems［R］.［S.l.］：Proceedings of the Royal Society，1957，41：376－396.

［12］刘恩儒，曾新吾.裂缝介质的有效弹性常数［J］.石油地球物理勘探，2001，36（1）：37－44.Liu Enru，Zeng Xinwu.Effiective Elastic Constant of Fractured Medium［J］.Oil Geophysical Prospecting，2001，36（1）：37－44.

［13］Liu E，Hudson J A，Pointer T.Equivalent Medium Representation of Fractured Rock［J］.J Geophys Res，2000，105（2）：2981－3000.

［14］Pointer T，Liu Enru，Hudson J A.Seismic Wave Propagation in Cracked Porous Media［J］.Geophys J Int，2000，142，199－231.

［15］Liu E，Hudson J A，Crampin S，et al.Seismic Properties of a General Fracture［EB/OL］（1995－10－05）［2012－03－29］.http：//www.eap.ac.uk/publications/papers/p1995/1995eliusc.pdf.

［16］Liu E，Chapman M，Zhang Z J，et al.Frequency Dependent Anisotropy：Effects of Multi－Fracture Sets on Shear－Wave Polarizations［J］.Wave Motion，2006，44（1）：44－57.