实现复频移完全匹配层吸收边界条件的递推卷积方法

田 坤，黄建平，李振春，李 娜，孔 雪，李庆洋

1.中国石油大学地球科学与技术学院，山东 青岛 266580

2.中石油东方地球物理公司研究院，河北 涿州 072750

0 引言

由于计算能力的快速发展，在过去几十年里对地震波在复杂介质中传播数值模拟方法的研究也越来越广泛和深入，其中应用最广泛的是有限差分法［1］。在有限差分算法中，计算模型不可能无限大，也就是模拟区域都是有界的，这样就需要在人工边界处对波进行吸收衰减。吸收边界条件有许多种，其中比较有效的是Bérenger［2］在电磁波模拟中提出的完全匹配层（perfectly matched layer，PML）吸收边界条件。其后Chew等［3］引入复数伸展坐标系对PML吸收边界条件进行公式化，指出PML的本质是在复数伸展坐标系中进行坐标变换。Rappaport［4］证明了PML介质等价于在吸收边界区域引入各向异性介质。近年来，PML吸收边界条件也被应用到声波和弹性波的有限差分正演模拟中［5－7］。大量研究［3，8］表明，PML 吸收边界条件比旁轴近似吸收边界条件［9］、Higdon吸收边界条件［10］、廖氏吸收边界条件［11］和指数衰减吸收边界条件［12］等具有更优越的吸收性能。此外，Teixeira等［13］和Chew等［14］在柱坐标系和球坐标系中实现了PML吸收边界条件。在国内，研究者对PML吸收边界条件也做了一些讨论［15－17］。

但是，传统的PML也存在一定的缺陷，离散后的PML反射系数不严格为0，尤其在大入射角的情况下更为严重；在这种情况下，相当一部分能量以反射波的形式被送回到主研究区域［18－20］。而大入射角的情况是普遍存在的，比如薄片区域、震源位置接近研究区域边缘、大偏移距接收等等。传统PML对窄区域的面波吸收也有一定的问题。为了克服这些问题，Kuzuoglu等［21］提出了复频移拉伸函数以改进坐标变换关系，在复频移拉伸函数中引入了额外的2个衰减参数，从而改善PML的吸收性能，称之为复频移PML（CFS－PML）。采用复频移拉伸函数后，PML算法不易用传统的分裂变量的形式实现，而不分裂变量计算卷积又大大增加计算成本。Drossaert等［22］提出了基于递归积分的不分裂复频移PML边界条件，实际上就是采用复频移拉伸函数，通过引入2个新的辅助张量，用递归积分的方法对其进行实现，从而避免直接计算卷积，减少计算量。张显文等［23］推导了基于递归积分的不分裂复频移PML弹性波方程交错网格高阶差分法，并对其进行了实现。Qin Zhen等［24］利用辅助差分方程技术实现了复频移PML的计算。无论是递归积分还是辅助差分方程，都可以在不分裂的情形下避免直接计算卷积，减少计算量；但是这2种方法推导过程复杂繁琐，不易实现。笔者推导了一种递推卷积方法，在交错网格情形下利用递推的形式计算卷积，推导过程直观易懂，易于编程，应用方便简单，计算成本没有太大变化。采用这种方法来求解弹性波方程，与常规PML的结果进行比较，可知，利用递推卷积计算的复频移PML能够有效地改善困难情况下的吸收效果，证明了本文方法的正确性和有效性。

1 基本原理

PML技术本质上是将波动方程在PML层内进行复坐标变换［3］。对于变换后的坐标，方程及其解的形式不变，但对于原坐标，解是衰减的。传统的PML中频率域坐标变换关系（以x方向为例）为

式中：sx是复拉伸函数；x是原坐标是变换后的坐标；ω是圆频率是衰减系数。复频移拉伸函数则是对式（3）进行了扩展，使其形式更一般化［19］：

其中：αx≥0；Κx≥1。可以看出，复拉伸函数是复频移拉伸函数在αx＝0、Κx＝1情况下的特例。

将坐标变换关系变换回时域，用sx（t）表示1/sx的傅里叶反变换，可以得到

可以看出，坐标变换在时域是卷积关系，重要的是如何避免直接计算卷积。

对式（4）取倒数并进行傅里叶变换可得

式中：δ（x）为冲激函数；H（t）为单位阶跃函数。

这样，时域坐标变换关系就分为2部分：其中第一部分容易计算，只要计算空间偏导除以系数Κ就可以了；最主要的是计算第二部分的卷积。

在离散情况下，将nΔt时刻的卷积写为［20］

由于采用交错网格，则

其中，

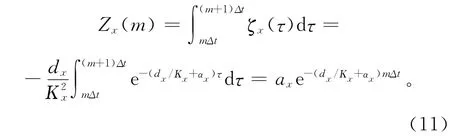
因为式（11）是简单的指数形式，所以可以把式（10）写成递推的形式：

其 中：为的简记形式；为的简记形式。

这样，在物理区域进行正常计算，在PML内通过下面的关系进行坐标变换后的计算就可以了：

其中，Ψx可以通过式（12）的递推得到。

值得注意的是，式（12）与（13）中的场变量在时间上不满足交错布局性。笔者采用如下策略：

1）首先进行坐标变换：

将式（12）代入式（14）可得

2）利用式（12）更新。

这就是复频移PML的递推卷积实现的基本原理。其实就是直接将卷积替换，在离散交错网格情形下通过递推计算，直观易懂，方便简单。它可以很容易地推广到y，z方向。4个角上的情形与传统的PML类似，所有方向同时考虑就可以了。

2 正演模拟计算与对比

2.1 模拟无限大区域时复频移PML和常规PML的吸收性能

为了验证本方法的正确性与有效性，对各向同性弹性介质进行了试算，并与传统的PML的计算结果进行了对比。所有算例均采用交错网格高阶有限差分法进行计算，时间二阶，空间六阶。图1是层状介质模型，采样点为301×301，网格间距5m×5 m，上层纵横波速度分别为3 000m/s、1 600m/s，下层纵横波速度分别为3 300m/s、1 900m/s，密度均为2 800kg/m3，震源网格点坐标为（150，5），为与z轴成逆时针135°夹角的集中力震源，道间距5 m，采样率0.5ms，采样时间1.5s。图2是震源主频为20Hz的z分量炮记录对比。如图中箭头所示，可以清楚地看到，常规PML的炮记录在远偏移距处有比较强的虚假反射，尤其是P－P反射波，其两翼已经完全畸变。这是由于在远偏移距处波入射到匹配层的入射角过大造成的。而复频移PML的炮记录则要干净很多，说明复频移PML对掠射情况下波的吸收效果比常规PML要好得多。为了更直观地观察，又对0.3s时的z分量波场快照进行了对比，如图3a、b所示。通过对比可以清楚地看到，黑框范围内，上界面附近远偏移距处，常规PML的波场快照有明显的反射能量，而复频移PML的波场快照则几乎看不到这一点。为了更清楚地显示，对上述波场快照的黑框部分进行放大，如图3c、d所示。通过二者的对比可以更清楚地看到上述现象（如图3中黑色箭头所示）。这进一步说明了复频移PML较常规PML能够有效地改善掠射情况下的吸收效果。

图1 层状介质模型Fig.1 Model of layer medium

为了更进一步说明这个问题，选择同样的速度模型，改变震源主频后进行了同样的计算对比。图4是震源主频为30Hz的z分量炮记录对比结果。可以看出：常规PML的炮记录在如图中黑色箭头所示的大偏移距处有比较强烈的假反射能量，而且随偏移距增加假反射能量越强烈；这是由于偏移距越大，波入射到匹配层的入射角越大，掠射情况越严重。而复频移PML比常规PML的吸收效果要更好一些。为了更好地说明，同样对0.3s时的z分量波场快照进行了对比，如图5所示。通过黑色方框和箭头所示区域的对比，也可以验证在掠射情况下复频移PML比常规PML吸收效果好。为验证上述结论，又抽取了3个单道在常规PML和复频移PML情况下0～1.2s和0.3～1.2s的波形进行了对比，如图6所示，图中3个单道与炮点纵坐标相同，而且随着横坐标数值的增大，与炮点距离增加，偏移距也就越大，相应地对匹配层的入射角也越大。从图6可以看到：在单道1常规PML和复频移PML的效果基本一样；但是在单道2，常规PML和复频移PML的波形开始出现明显的区别，常规PML的波形产生了一些不应该有的虚假震荡；在单道3二者的差别更加明显，常规PML的虚假震荡也更大。这也说明了在远偏移距处即大入射角的情况下复频移PML比常规PML吸收效果好；而且随着偏移距增大，入射角增加，效果对比更加明显，常规PML中的虚假反射影响更加严重。

以上结论可与文献［22－24］中的结果进行类比，结论相似；尤其是与文献［24］，结果基本一致。这是因为这几种方法在坐标变换中都是采用相同的复频移拉伸函数，所不同的只是实现方法。相较而言，本文方法更直观易懂，易于编程；而且本文模拟震源接近研究区域边缘的情况而非长条形介质，更符合大多数的实际情况。

图2 主频为20Hz的炮记录对比Fig.2 Comparison of seismogram when dominant frequency is 20Hz

图3 主频为20Hz的0.3s波场快照及局部放大图Fig.3 Snapshot and its partial enlarged detail of 0.3swhen dominant frequency is 20Hz

图4 主频为30Hz的炮记录对比Fig.4 Comparison of seismogram when dominant frequency is 30Hz

图5 主频为30Hz的0.3s波场快照及局部放大图Fig.5 Snapshot and its partial enlarged detail of 0.3swhen dominant frequency is 30Hz

为考察掠射情况下常规PML的虚假反射对复杂介质波场尤其是绕射等弱能量波场的影响以及复频移PML在这种情况下的吸收性能，对含散射体的两层介质模型进行了计算对比。图7是含散射体介质模型，在网格点坐标（225，15）即近地表处有一散射体，散射体纵横波速度分别为2 700、1 300m/s，其他参数与前相同。图8是震源主频为30Hz的z分量炮记录对比。如图中黑色箭头所示，可以清楚地看到常规PML的炮记录在两翼有很强的虚假反射能量，严重影响炮记录的质量；尤其是绕射波，由于能量较弱，相对来说对其的影响更严重，如直达纵波的绕射横波右翼，畸变就比较严重，而直达横波的绕射纵波右翼，则几乎被掩盖。复频移PML的炮记录相对来说就好很多，各个波形都很清楚，这也说明了复频移PML较常规PML的效果优势。图9是0.3s时的z分量波场快照对比，也可以看出常规PML在掠射情况下产生的比较强的虚假反射对绕射波等弱能量波场有相当的影响，这会对实际应用中的成像、反演等其他处理产生不利影响，而复频移PML则会改善这一点。

2.2 复频移PML与常规PML的计算量与存储量

二维情况下，在存储量方面，对于分裂的常规PML来说，如果不存储总波场，那么需要存储数组的最大个数是10。但是，每次循环都需要由分裂的波场分量相加计算总波场。如果存储总波场，则所需要存储的数组最大个数为15。对于不分裂的复频移PML来说，所需存储的数组最大个数为13，与常规PML相比没有太大变化。在计算量方面，不存储总波场的常规PML计算时间为295s，复频移PML计算时间为213s。硬件条件相同，CPU为英特尔E8400，主频3GHz。可见，复频移PML的计算量由于不分裂而有所减少。

图6 不同单道的复频移PML和常规PML波形对比Fig.6 Wave contrast figure of different receivers between CFS－PML and classical PML

2.3 窄区域自由表面条件下PML和复频移PML对面波的吸收性能

由于越来越高的工程研究和实际应用要求，对自由表面条件下近地表地震波传播的模拟是重要和基本的。瑞雷波相速度与频率的关系已经被广泛地用于浅层横波速度估计中［25］。因此，产生包含准确瑞雷波信息的合成地震记录是任何近地表地震模拟的首要目标。然而，在含传统PML的数值模拟中，如果模拟区域顶部自由表面距离底部的PML比较近，由于低频瑞雷波的传播方向与底部PML的走向基本平行，瑞雷波在传播过程中会与底部PML相互作用，降低吸收效果，甚至产生不稳定性［26］。复频移PML同样会改善这一点。下面以带自由表面的各向同性弹性均匀介质为例进行说明。模型大小为15km×1km，密度为2 700kg/m3，纵横波速度分别为3 200m/s、1 870m/s，震源采用主频为2.5Hz的雷克子波，置于靠近左边界距自由地表0.15km的地方。图10是不同时刻的z分量波场快照对比。2s时面波正要和体波分开，可以看出两者结果几乎没有差别，但是图10a左边有一些轻微的干扰噪音。这是由于震源太靠近左边界，大量能量突然进入匹配层，传统PML吸收不完全所致，这也说明了复频移PML比传统PML吸收效率要高。6s时面波已在介质中传播相当一段距离并与体波完全分离，可以看出图10c中面波已经有所畸变并在其后面产生了一些虚假波形；这是由于面波与底部PML相互作用，降低吸收效果，并影响到物理区域的缘故。而图10d中复频移PML的吸收效果就很好，瑞雷面波的特征得到了保持。

图7 含散射体介质模型Fig.7 Layer media model with scatterer

3 结论与讨论

1）常规PML在离散后反射系数不为0，尤其在大入射角、大偏移距的情况下会产生很强的假反射，降低吸收效果，对真实波场产生比较严重的影响，这种影响随入射角、偏移距的增加而增大。

2）基于递推卷积的复频移PML技术能够增强掠射情况的波场衰减，降低反射系数，有效改善匹配层的吸收效果。

3）对于含散射体的复杂介质模型，常规PML也会产生假反射，并更加严重地影响散射场等弱能量波场，而且会对实际应用中的偏移、反演等处理产生不利影响；而基于递推卷积的复频移PML技术同样可以改善吸收效果，降低不利影响。

4）对于窄区域自由表面条件下面波的模拟，传统PML也会对波场产生比较严重的影响，而基于递推卷积的复频移PML同样会改善这一点。

5）基于递推卷积的复频移PML技术采用不分裂变量的递推卷积方法进行计算，实现时通过递推来计算卷积，使其存储量和计算量与常规PML相比都没有太大变化，不会增加计算成本。

图8 含散射体模型的z分量炮记录对比Fig.8 Comparison of z component seismogram of the model with scatterer

图9 含散射体模型的z分量0.3s波场快照及局部放大图对比Fig.9 Comparison of z component snapshot and its partial enlarged detail of 0.3s

本文基于递推卷积的复频移PML技术能够有效改善传统PML在困难情况下的吸收效果，而且不增加计算成本，这对很多如薄片区域、震源接近研究区域边缘、大偏移距接收的体波模拟和窄区域的面波模拟等情况有很好的应用前景。对于偏移成像等处理中的吸收边界条件，这也是一种较好的选择。但是复频移PML没有改变常规PML的基本思想，所以它还是存在一些问题，比如对一些各向异性介质有固有的不稳定性、离散后匹配层反射系数不严格为0等不足还是不能很好地克服。笔者在匹配层外围采用的是Dirichlet边界条件，后续研究中可以将其替换为旁轴吸收边界条件以进一步提高离散后的吸收效果；另外对于二阶位移波动方程的复频移PML吸收边界条件也有待进一步研究。基于递推卷积的复频移PML技术以及后续相关方法的进一步研究，将有利于西部碳酸盐岩探区复杂近地表速度模型下的正演模拟，尤其是对碳酸盐岩探区近地表散射波机理认识的研究，为将来碳酸盐岩探区高精度勘探开发服务。

图10 带自由地表模型的z分量波场快照对比Fig.10 Comparison of z component snapshots with free surface

（References）：

［1］Virieux J.P－SV Wave Propagation in Heterogeneous Media：Velocity－Stress Finite－Difference Method［J］.Geophysics，1986，51（4）：889－901.

［2］Bérenger J P.A Perfectly Matched Layer for the Absorption of Electromagnetic Waves［J］.Journal of Computational Physics，1994，114（2）：185－200.

［3］Chew W C，Weedon W H.A 3－D Perfectly Matched Medium from Modified Maxwell’s Equations with Stretched Coordinates［J］.Microwave and Optical Technology Letters，1994，7（13）：599－604.

［4］Rappaport C M.Perfectly Matched Absorbing Boundary Conditions Based on Anisotropic Lossy Mapping of Space［J］.IEEE Microwave Guided Wave Lett，1995，5（3）：90－92.

［5］Liu Q H，Tao J P.The Perfectly Matched Layer for Acoustic Waves in Absorptive Media［J］.Journal of the Acoustical Society of America，1997，102（4）：2072－2082.

［6］Wang T，Oristaglio M L.3－D Simulation of GPR Surveys Over Pipes in Dispersive Soils［J］.Geophysics，2000，65（5）：1560－1568.

［7］Zeng Y Q，He J Q，Liu Q H.The Application of the Perfectly Matched Layer in Numerical Modeling of Wave Propagation in Poroelastic Media［J］.Geophysics，2001，66（4）：1258－1266.

［8］Chen Y H，Chew W C，Oristaglio M L.Application of Perfectly Matched Layers to the Transient Modeling of Subsurface EM Problems［J］.Geophysics，1997，62（6）：1730－1736.

［9］Engquist B，Majda A.Absorbing Boundary Conditions for the Numerical Simulation of Waves［J］.Mathematics of Computation，1977，31：629－651.

［10］Higdon R L.Absorbing Boundary Condition for E－lastic Waves［J］.Geophysics，1991，56（2）：231－241.

［11］Liao Z P，Wong H L，Yang B P，et al.A Transmitting Boundary for Transient Wave Analysis［J］.Scientia Sinica，1984，27（10）：1063－1076.

［12］Marfurt K J.Accuracy of Finite－Difference and Finite－Element Modeling of the Scalar and Elastic Wave Equations［J］.Geophysics，1984，49（5）：533－549.

［13］Teixeira F L，Chew W C.On Causality and Dynamic Stability of Perfectly Matched Layers for FDTD Simulations［J］.IEEE Transactions on Microwave Theory and Techniques，1999，47（6）：775－785.

［14］Chew W C，Liu Q H.Perfectly Matched Layers for Elastodynamics：A New Absorbing Boundary Condition［J］.Journal of Computational Acoustics，1996，4（3）：341－359.

［15］刘四新，曾昭发，徐波.地质雷达数值模拟中有损耗介质吸收边界条件的实现［J］.吉林大学学报：地球科学版，2005，35（3）：378－381.Liu Sixin，Zeng Zhaofa，Xu Bo.Realization of Absorbing Boundary Condition with Lossy Media for Ground Penetrating Radar Simulation［J］.Journal of Jilin University：Earth Science Edition，2005，35（3）：378－381.

［16］殷文.基于频率域高阶有限差分法的正演模拟及并行算法［J］.吉林大学学报：地球科学版，2008，38（1）：144－151.Yin Wen.Forward Modeling and Parallel Algorithm Based on High－Order Finite－Difference Method in Frequency Domain［J］.Journal of Jilin University：Earth Science Edition，2008，38（1）：144－151.

［17］韩利，韩立国，李翔，等.二阶声波方程频域PML边界条件及频域变网格步长并行计算［J］.吉林大学学报：地球科学版，2011，41（4）：1226－1232.Han Li，Han Liguo，Li Xiang，et al.PML Boundary Conditions for Second－Order Acoustic Wave Equations and Variable Grid Parallel Computation in Frequency－Domain Modeling［J］.Journal of Jilin University：Earth Science Edition，2011，41（4）：1226－1232.

［18］Festa G，Vilotte J P.The Newmark Scheme as Velocity－Stress Time－Staggering：An Efficient PML Implementation for Spectral－Element Simulations of Elastrodynamics［J］.Geophysical Journal International，2005，161：789－812.

［19］Roden J A，Gedney S D.Convolution PML（CPML）：An Efficient FDTD Implementation of the CFS－PML for Arbitrary Media［J］.Microwave and Optical Technology Letters，2000，27（5）：334－339.

［20］Komatitsch D，Martin R.An Unsplit Convolutional Perfectly Matched Layer Improved at Grazing Inci－dence for the Seismic Wave Equation［J］.Geophysics，2007，72（5）：SM155－SM167.

［21］Kuzuoglu M，Mittra R.Frequency Dependence of the Constitutive Parameters of Causal Perfectly Matched Anisotropic Absorbers［J］.IEEE Microwave and Guided Wave Letters，1996，6（12）：447－449.

［22］Drossaert H F，Giannopoulos A.A Nonsplit Complex Frequency－Shifted PML Based on Recursive Integration for FDTD Modeling of Elastic Waves［J］.Geophysics，2007，72（2）：T9－T17.

［23］张显文，韩立国，黄玲，等.基于递归积分的复频移PML弹性波方程交错网格高阶差分法［J］.地球物理学报，2009，52（7）：1800－1807.Zhang Xianwen，Han Liguo，Huang Ling，et al.A Staggered－Grid High－Order Difference Method of Complex Frequency－Shifted PML Based on Recursive Integration for Elastic Wave Equation［J］.Chinese Journal of Geophysics，2009，52（7）：1800－1807.

［24］Qin Z，Lu M H，Zheng X D，et al.The Implementation of an Improved NPML Absorbing Boundary Condition in Elastic Wave Modeling［J］.Applied Geophysics，2009，6（2）：113－121.

［25］Socco L V，Foti S，Boiero D.Surface－Wave Analysis for Building Near－Surface Velocity Models－Established Approaches and New Perspectives［J］.Geophysics，2010，75（5）：A83－A102.

［26］Festa G，Delavaud E，Vilotte J P.Interaction Between Surface Waves and Absorbing Boundaries for Wave Propagation in Geological Basins：2DNumerical Simulations［J］.Geophysical Research Letters，2005，32：L20306.