安徽省矿点分布与主要形迹相关性的分形研究

施国栋,靳保路,陈 斌

(1.安徽建筑大学 土木工程学院,合肥 230601;2.建筑健康监测与灾害预防技术国家地方联合工程实验室,合肥 230601;3.河海大学 地球科学与工程学院,南京 210098;4.浙江展图建设有限公司,杭州 311600)

自1967年Mandelbrot首次提出分形概念,分形理论在研究非线性系统中得到了非常广泛的应用,成为非线性学科的前沿,并应用于岩石学、工程地质、水系、地质灾害、成矿规律、成矿预测等研究中[1-9],并成为地质矿产界在点和形迹研究领域的一场“革命”。矿点分布在宏观上表现出杂乱无章,但是却蕴藏着大量的分形现象,杂乱而有序,无章可定量[10-15]。分形理论不仅可以改变对矿点分布的传统认识,而且对矿产资源预测有了全新的方法并产生重要影响。安徽省成矿地质条件优越,成矿模式、成矿规律和成矿系列划分多样,矿产资源分布呈现种类多、分布广的特点,利用分形理论可以发现矿产资源总体分布的规律性,并将其与安徽省内主要形迹水系和断裂的分形特征联系起来,寻找分形联系。

为了解决安徽省矿点分布与主要形迹相关性问题,首次将分形理论的方法应用于安徽省矿点分布的研究中,采用分形理论中的“盒维数法”对安徽省矿点分布的分形特征进行研究。以1∶50万的安徽省矿点分布图为底图,进行矢量化处理和网格剖分,将安徽省区域划分成256个子区域,计算出了每个小区域内的矿点分维值。同理， 计算出了每个小区域内的安徽省主要形迹水系和断裂分维值,绘制其等值线图,分析矿点分布与主要形迹的相关性。应用分形理论,在“杂乱无章”的矿点分布中研究其规律性及其与其他“杂乱”形迹的相关性,具有一定的现实意义和应用价值。

1 研究区概况

安徽省有着十分优越的地理条件,矿产资源丰富,为长三角地区发展提供了重要的矿产资源,是国家中部崛起战略实施的重要发展区域,且矿产资源拉动着安徽省国民经济高速发展。 截至2015年底, 已发现矿产158种(含亚种), 列入资源储量表89种, 煤炭、 铜矿、 铁矿是该省优势矿产, 主要矿产分布呈“北煤、 中铜铁、 南钨”的空间格局, 全省查明资源储量的固体矿产地1 437处, 其中大型矿床241处、中型矿床297处、小型矿床389处、小型以下矿产地510处。主要矿产资源在1∶50万的安徽省矿点分布图中标识矿点257处。2015年,全省矿石总产量4.65亿t,采矿业产值798亿元。全省规模以上矿山采选业及相关能源、矿产品加工制造业等矿业经济总产值1.26万亿元,占全省工业总产值的31.64%[16]。

2 分形分维的引入

分形分维的测定目前经常采用的算法有码尺法、自仿射分形法、幂律谱法、周长-面积关系法和盒维数法等5种方法。本文涉及不同尺度下的矿点和形迹线的统计分析,盒维数法在统计点线分维值方面准确直观、操作性强,故采用该法。盒维数法又称数格子法和网络覆盖法,即使用不同尺度的边长为r的正方形网格(或称之为盒子)去覆盖所要计算的形迹底图(边长为L),分别计量在不同尺度下得到的盒子数N(r) 及分维值D[17-19]。

N(r)∝r-D,

(1)

(2)

分别以边长为r=L/2、L/4、L/8、L/16和L/32的正方形网格覆盖安徽省矿点图和主要形迹图, 统计在各尺度网格下有矿点和形迹的格子数N(r), 绘制成lnN(r)-lnr的散点图, 根据式(1)、 (2), 利用最小二乘法对散点进行拟合分析, 拟合的直线斜率绝对值即为分维值D。若对任意的δ>0,N是能覆盖S的最小网格数, 取不同大小的δ, log(1/δ)的值由小到大排列, 计算出不同的logN值, 再根据D=logN/log(1/δ)计算出记盒维数序列, 以log(1/δ)为横轴、 logN为纵轴, 找出平面上点集的最佳逼近直线的斜率即为所求。

3 矿点分布与主要形迹相关性的分形

3.1 安徽省矿点分布分形特征

将安徽省1∶50万矿产资源分布图中的257个矿产资源分布点矢量化,以L=570 km为正方形底图,然后划分为2×2格(r=285 km)、 4×4格(r=142.5 km)、 8×8格(r=71.25 km)、 16×16格(r=35.625 km)和32×32格正方形(r=17.812 5 km), 依次统计出包含矿点的格子数N(r)(图1、 表1), 以lnr为横坐标、 lnN(r)为纵坐标, 用表1得到的5组数据, 拟合得安徽省矿点分形拟合方程为y=-1.337 1x+9.158 4, 故分维值D=1.337 1, 相关性系数R2=0.981 7(图2), 分形相关性强, 表明安徽省整体矿点分布具有明显的分形特征。 本文矢量化的安徽省矿点,虽然没有区分图中各个矿点之间的种类和成因区别,但是这种明显的分形特征,又蕴含着同样程度下种类的多样性和成因的复杂性,说明矿点在安徽省区域内的分布是自相似的,而且局部分布与安徽省整体分布具有显著的相似性。

图1 安徽省矿点分形计算网格图Fig.1 Grid of fractal calculation of ore spots in Anhui

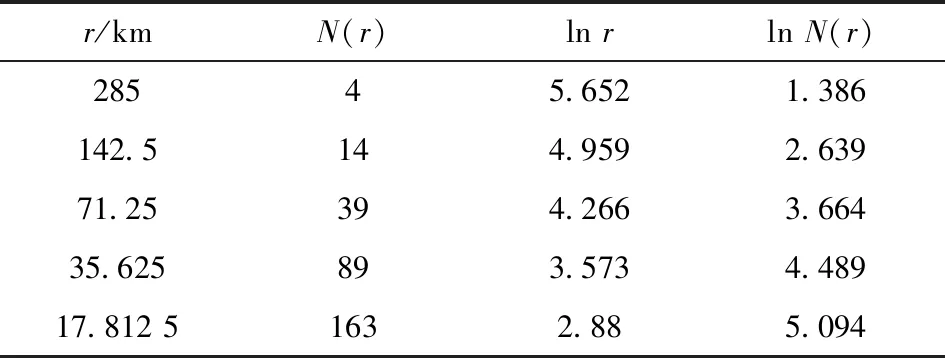
表1 安徽省矿点盒维数统计Table 1 Statistics of ore spots box dimension in Anhui

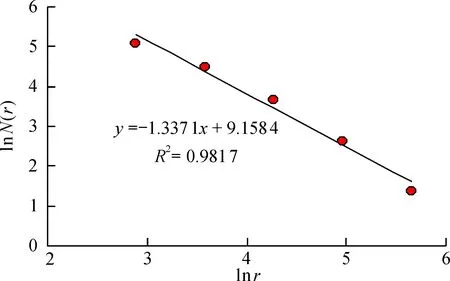
图2 矿点分形拟合结果Fig.2 Fractal fitting results of ore spots

3.2 矿点分布与水系相关性的分形分析

矿点的分布与地质构造、岩石性质、地壳运动和岩浆活动等因素有关, 因此可从分布明显的形迹水系和断裂构造中寻找与矿点分布之间的关系。

同样,运用盒维数法计算拟合方程得到安徽省总体水系(图3)的分维值为1.582 5(表2),主要的水系淮河、长江和新安江,其分维值依次是1.383、1.331和1.02,表明水系的发育以淮河水系最复杂,长江水系次之,新安江最简单且与淮河及长江水系分维值差值大。而三水系在安徽省内流域面积依次为6.69万、6.6万、0.65万km2,这与实际的安徽省水系及三水系的分布发育整体情况一致。各水系的分维相关系数R2均大于0.9,表明各水系本身就具有显著的分形特征,与Mandelbrot最初研究的英国海岸线的分形特征原理极为相似,分维值越高表明水系越发育的趋势。通过对比本文的数据及他人对水系研究的数据,安徽省的水系分维值1.582 5,高于全国的的水系分维值1.418 9[20],表明安徽省的水系相对全国来说是非常发育的,这与安徽省内有淮河和长江两大水系横贯其中有关。

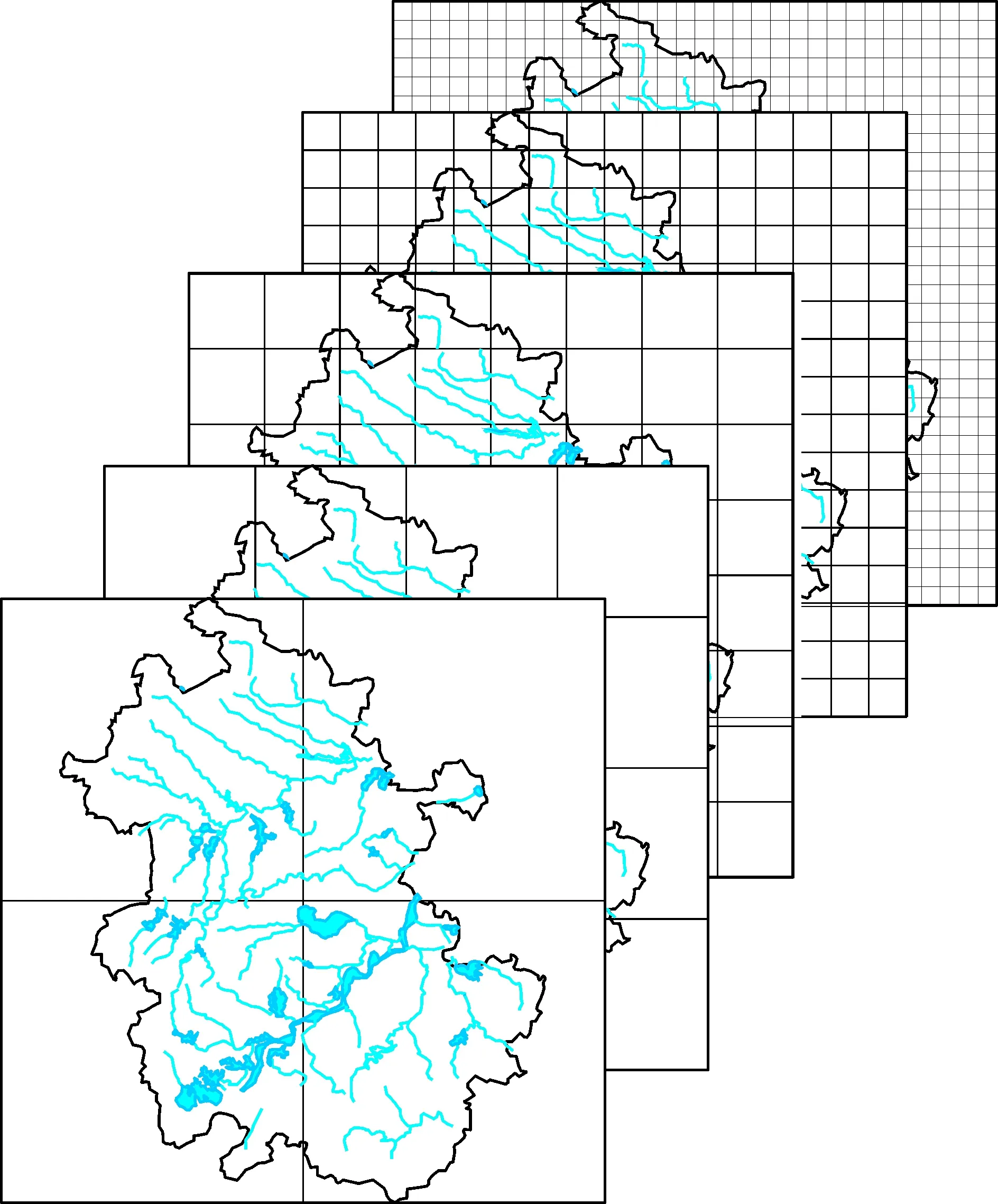
图3 安徽省水系分形计算网格图Fig.3 Grid of fractal calculation of water systems in Anhui

淮河水系发育复杂, 分维值最高(1.383), 包含矿点数86个; 长江水系分维值为1.331, 稍低于淮河, 包含矿点数却为165个; 新安江水系发育最简单, 分维值为1.02最低, 包含矿点数仅为6个。 说明安徽省境内水系的分维值与矿点的分布不是正比关系, 水系分维值在1.3左右(本文计算的分维值1.331, 朱晓华等计算的分维值为1.329 2[20], 孟宪萌等计算的分维值为1.386[22]), 矿点分布点数最多(表2)。 水系分维值可以反映水系所处流域地貌侵蚀发育程度和构造活动性的强弱[23], 而地貌侵蚀发育程度又与风化型矿产资源相关联, 如长江水系所处地层中发育沉积型锰矿及其风化后形成的氧化锰矿, 强烈的河流地质作用, 又使得大量的矿产资源外露, 有色金属矿产、 非金属矿产相对集中。 安徽省矿产资源分布点的分维值1.337 1与长江水系的分维值1.331最接近, 表明安徽省的矿产资源分布受长江水系影响明显, 且安徽省内分维值在1.3～1.4的水系有利于成矿。

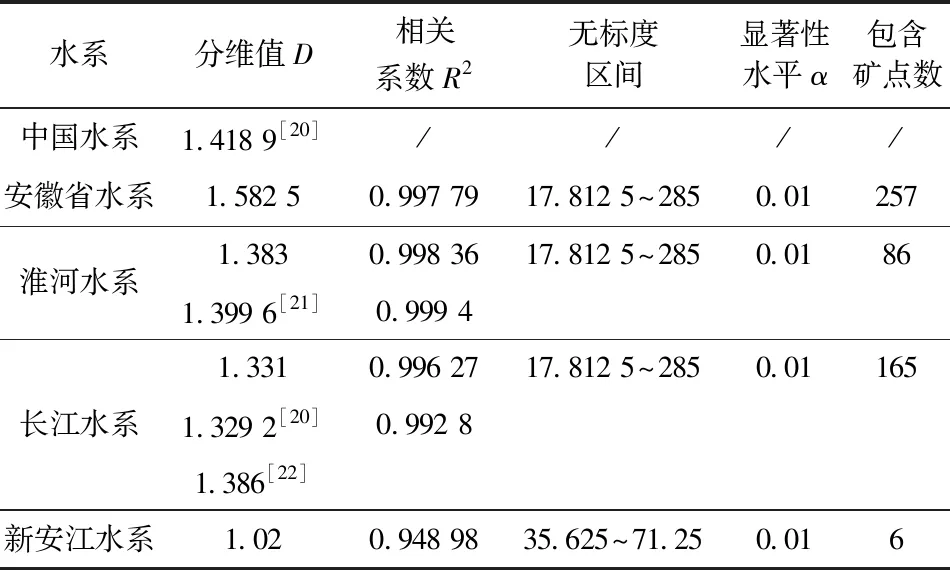
表2 主要水系空间分布分维值比较Table 2 Comparison of fractal dimension values of spatial distribution of main river systems

3.3 矿点分布与主要断裂相关性的分形分析

同理,将断裂底图划分为2×2、 4×4、 8×8、 16×16和32×32格正方形, 依次统计出包含矿点的格子数N(r)(图4、 表3), 以lnr为横坐标、 lnN(r)为纵坐标, 得到安徽省断裂的分形拟合方程为y=-1.568 4x+10.338, 分维值D=1.568 4, 相关性系数R2=0.997 6(图5), 相关性强, 具有显著的分形特征。 安徽省断裂分维值(1.568 4)大于矿产资源分布点分维值(1.337 1),故在此基础上可对两者的关系从分维角度作进一步的分析。

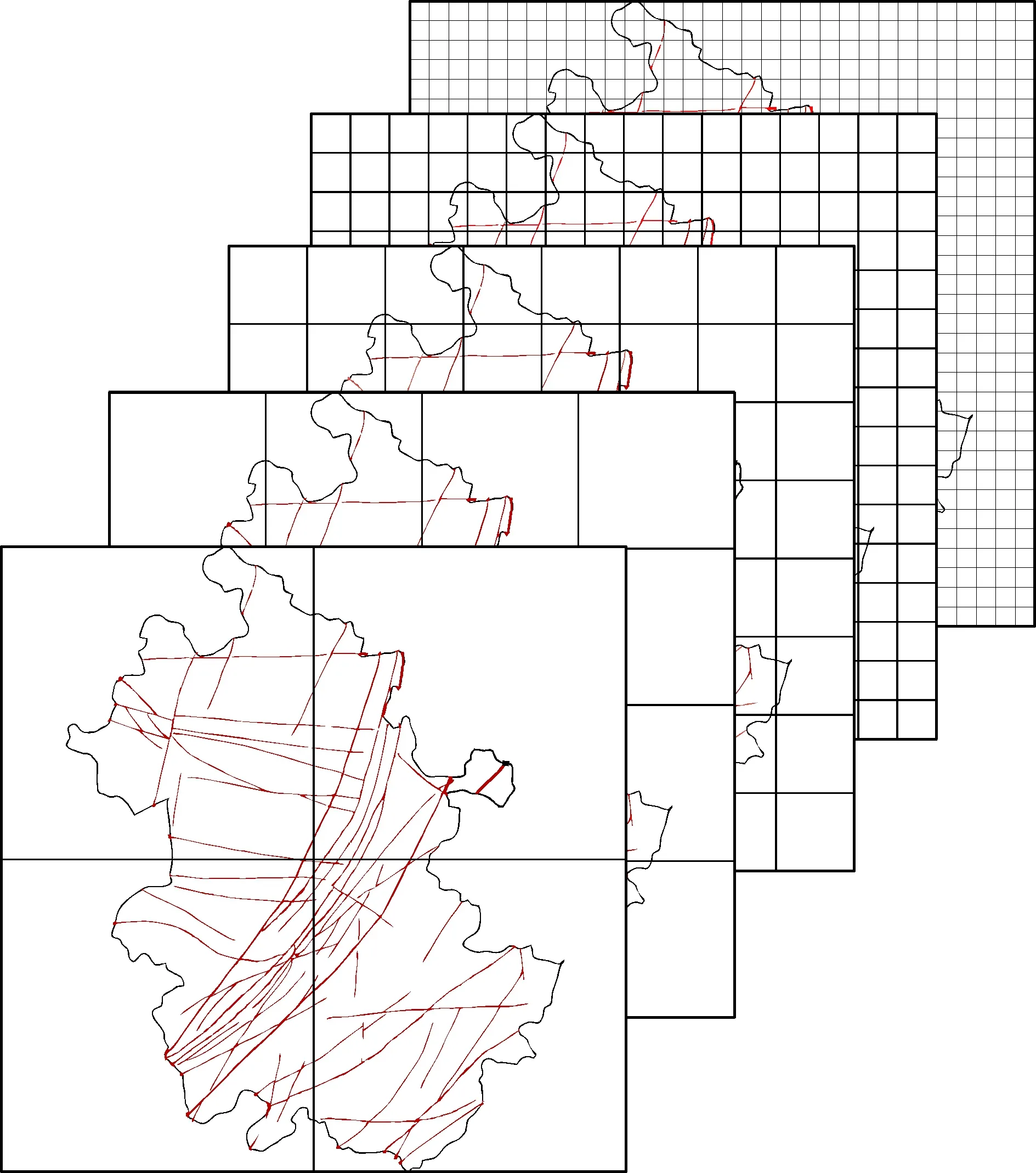
图4 安徽省主要断裂分形网格图Fig.4 Fractal grid of main faults in Anhui

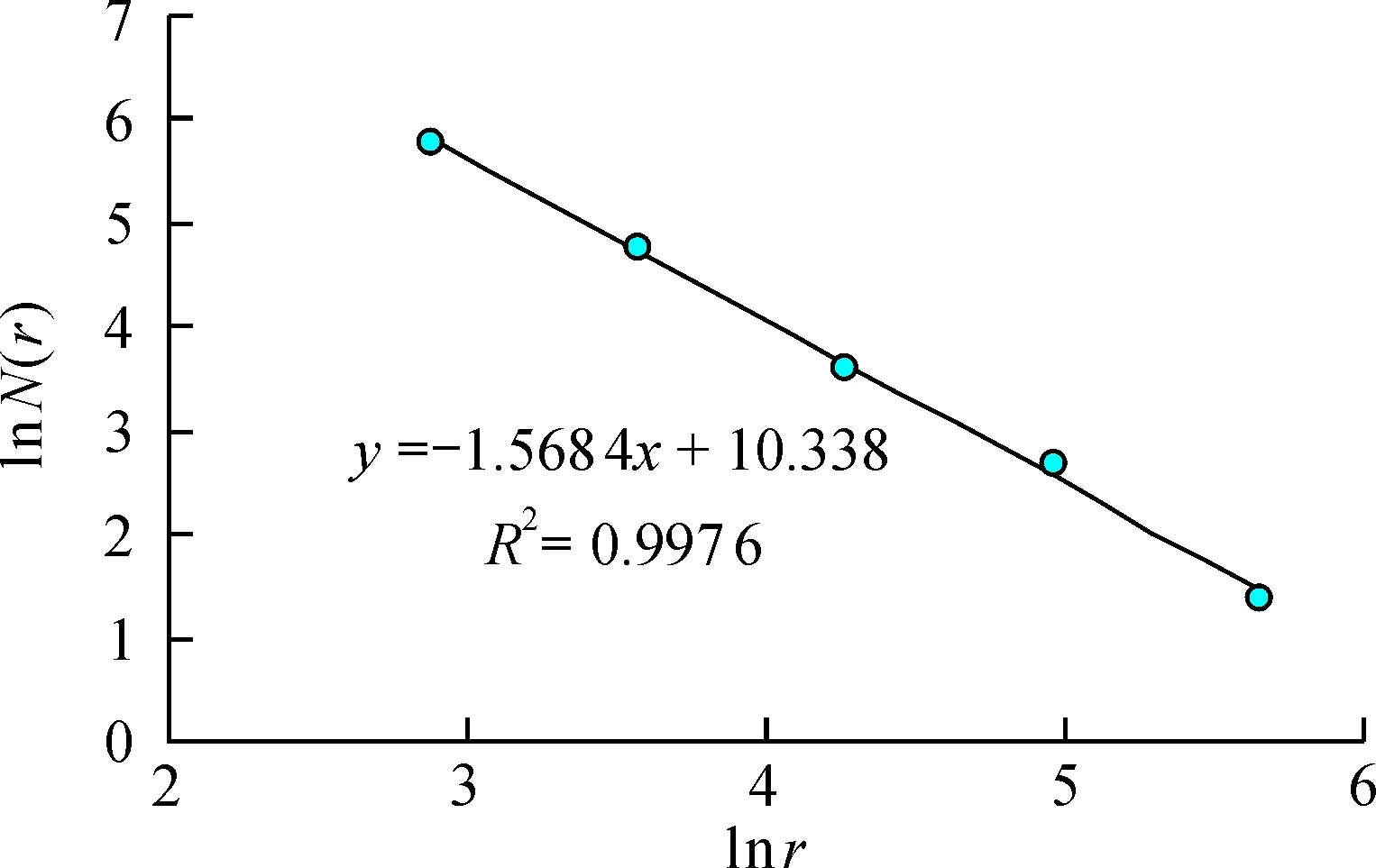
图5 断裂分形拟合结果Fig.5 Fractal fitting results of fracture

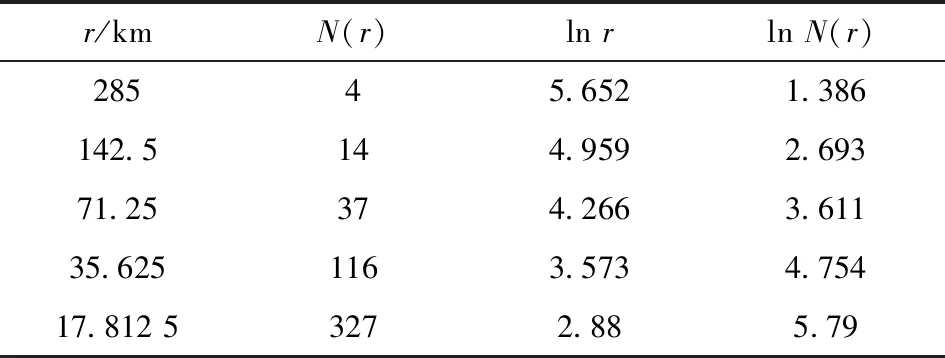
表3 安徽省主要断裂构造盒维数统计Table 3 Statistis of box dimensions of major faults in Anhui

对断裂形迹和矿点分布情况两者都用盒维数法计算出各个分维值后,用16×16的小正方形覆盖安徽省断裂图及矿点分布图,将这256个区域的断裂、矿点用盒维数法计算出各个分维值,将数据网格化导入到Surfer 软件中作分维值的等值线图,形成断裂构造分维等值图(图6a)和矿点分维等值图(图6b)。 提取断裂和矿点分布的分维值均大于1.0的等值线, 发现在安徽省内矿点分布形成了6个D≥1.0的独立区域,且与断裂分维值高值基本吻合。 安徽省断裂分维值(1.568 4)与矿产资源分布点分维值(1.337 1)差异大, 表明安徽省内的矿产资源分布主要不是受断裂控制的, 但是在高分维值区域,两者之间又存在联系。

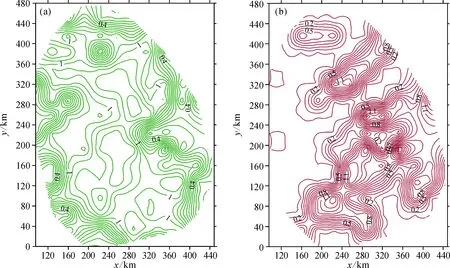
图6 断裂构造(a)及矿点(b)分维等值线图Fig.6 Fractal contour of fault(a) and ore spot(b)

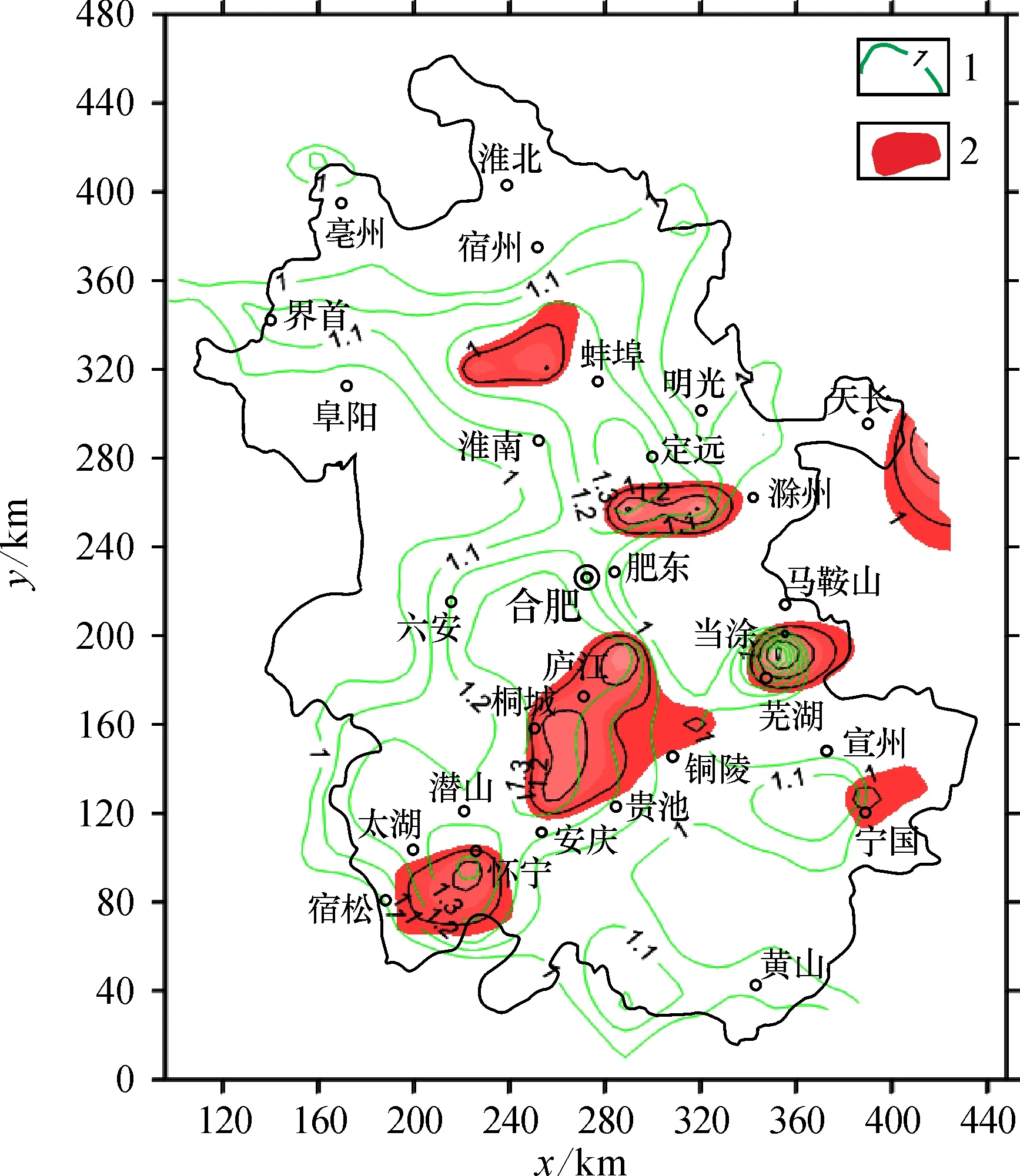
图7 断裂及矿点分维等值线(D≥1.0)叠加处理结果Fig.7 Superposition of fractal dimension isoline (D≥1.0) of faults and ore spots1—断裂分维等值线; 2—高维叠加区

为了进一步揭示断裂和矿点分布的关系, 在矿点分布分维值大于1.0的底图中(图7),将安徽省断裂构造分维等值图以D≥1.0、≥1.1、≥1.2、≥1.3和≥1.4作出5个层次图,与矿点分布分维值进行关联。通过Surfer 11计算上述5个范围的分维区间下断裂构造区域面积及其与矿点分布D≥1.0区域的重叠面积(表4、 图8)。

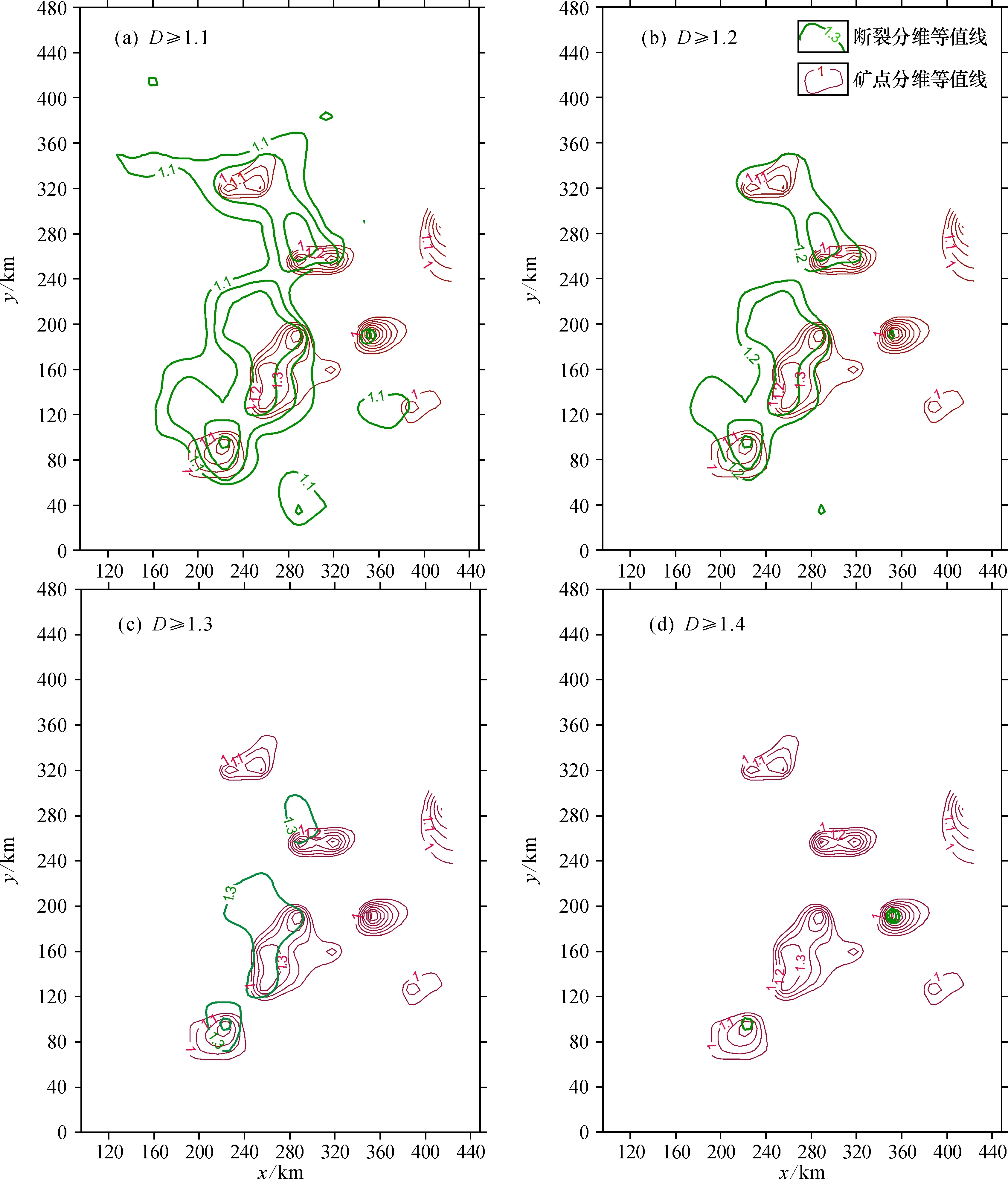
图8 断裂构造不同分维值(D≥1.1、 1.2、 1.3、 1.4)等值线图Fig.8 Contour maps of fault structures for different fractal dimension values(D≥1.1, 1.2, 1.3, 1.4)

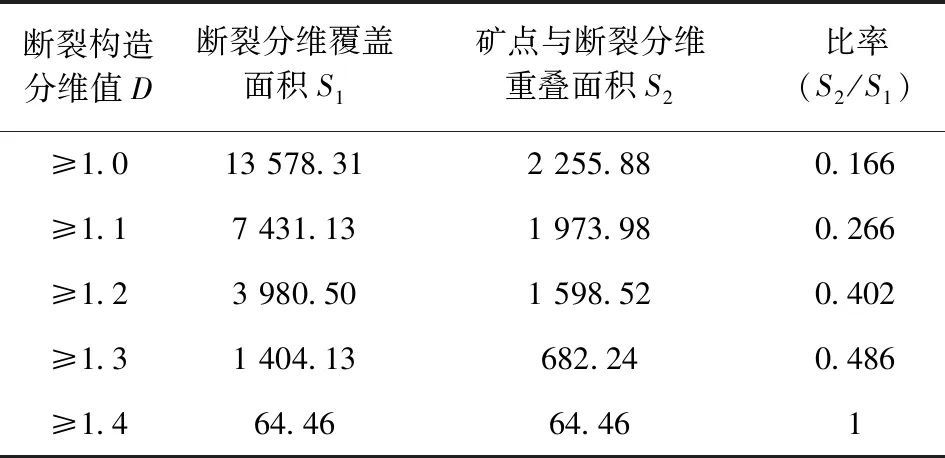
表4 不同断裂分维区间下矿点分布比例Table 4 Distribution proportion of ore spots under different fault fractal dimension intervals

由表4、图9可知,随着断裂构造分维值增大,分维值覆盖区域的不断缩小,其断裂分维所覆盖的面积与矿点分布(D≥1.0)面积的比率越大； 在D≥1.4时，其比率达到1,覆盖面积相同。故断裂高分维值区域且分维值D≥1.4,一定是矿点分布的高分维区,且分形特征明显,即矿点分布密集。从分形角度可理解为，分维值高的矿点分布区一定是受断裂控制,但分维值低的矿点不一定完全是由断裂控制。通过比对安徽省矿产资源分布图的地理位置发现, 庐江、宁国一带,怀宁以南, 定远以南,芜湖以北,淮南北部等地是矿点受断裂构造影响强烈区。此外， 在断裂构造最复杂处存在某一类型高分维矿点与之对应,即此处矿点受断裂构造影响最强烈,对比矿产资源图的地理位置为定远以南的铜矿,表明该处铜矿受构造控制,符合该处铜矿床断裂构造控矿模式。故通过分形分维结果,可知安徽省内总体矿点的分布不是主要受断裂控制的,但当断裂分维值D≥1.4时,对应安徽省矿点分布的高分维区,表明分维值高的矿点一定是受断裂控制的。

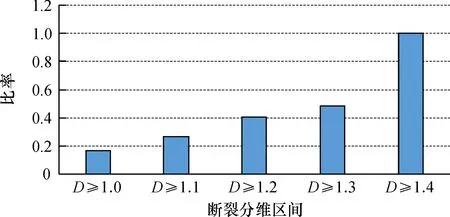
图9 不同断裂分维区间下矿点分布比例Fig.9 Distribution proportion of ore spots in different fault fractal dimension intervals

4 结 论

利用分形理论计算了安徽省矿点分布的分形值,从分形的角度建立了安徽省内主要形迹水系和断裂与矿点分布的关系。

(1)安徽省矿点分布的分维值D=1.337 1,相关系数R2=0.981 7,矿点分布具有显著的分形特征。

(2)安徽省总体水系的分维值D=1.582 5,主要水系淮河、长江和新安江的分维值依次是1.383、1.331和1.02,安徽省矿产资源分布点的分维值1.337 1与长江水系的分维值1.331最接近,表明安徽省的矿产资源分布受长江水系影响明显,且分维值在1.3～1.4的水系有利于成矿。水系分维值可以反映水系所处流域地貌侵蚀发育程度,而地貌侵蚀发育程度又与风化型矿产资源相关联;强烈的河流地质作用, 又使得大量的矿产资源外露,有色金属矿产、非金属矿产相对集中。

(3)安徽省断裂分维值为1.568 4,与矿点分布的分维值1.337 1差异大,说明安徽省矿点分布受断裂影响不大； 但当断裂分维值D≥1.4时,对应安徽省矿点分布的高分维区,表明分维值高的矿点一定是受断裂控制,且分形特征明显。断裂高分维值区与矿点分布的高分维区完全重叠,为矿点受断裂构造影响最强烈区,表明该处为断裂构造控矿模式。

(4)分形理论可以成为成矿预测、成矿模式研究和矿产资源规划的重要的方法,尤其在研究看似杂乱无章的矿点分布规律上显得非常有价值。