基于GA-PSO-BP的大坝变形监测模型

卢献健,罗 乐,胡应剑,周 斌,王 雷

(1.桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541006;2.广西壮族自治区地理信息测绘院,广西 柳州 545006)

大坝自动监测资料能够有效反映大坝的现役性态, 实际应用中常对实测大坝变形监测资料建立统计模型以便实时监控及变形预测[1-2]。 然而大坝变形监测数据具有较强的非平稳性和非线性, 且多源监测数据的分析处理对数学模型提出了更高的要求, 传统模型或单一模型因学习效率低或易陷入局部极值等问题而难以达到预测要求[3-6]。 徐锋等[7]采用粒子群算法(PSO)优化BP神经网络, 克服了BP网络模型连接权值和阈值的随机性, 但在粒子寻优过程中PSO算法存在陷入局部极值的缺陷。 邢尹等[8]成功地将遗传算法(GA)应用于BP神经网络学习中, 虽然解决了BP网络模型易陷入极值的缺点, 但是由于GA算法复杂的遗传操作, 使得神经网络训练时间随着种群的规模呈指数增长, 导致寻优时间过长; 而且GA算法对局部区域的搜索能力较差, 在接近最优解时容易出现收敛缓慢或停止的现象。

针对上述两种算法的缺陷, 本文以PSO算法为主, 将GA算法中的交叉、 变异操作引入了PSO算法中, 通过逐次迭代取最优结果的方式, 确定网络模型的最优连接权值和阈值, 代替了BP神经网络的学习过程, 使BP网络学习的输出误差最小化, 提高神经网络的性能, 并将其用于大坝变形分析实例中, 最后通过实验验证模型的正确性及有效性。 本研究可为大坝等变形监测的数据处理提供新的思路与参考。

1 基于GA-PSO算法的粒子寻优

粒子群优化(PSO)算法中粒子运动的过程表示如下:

假设粒子搜索的空间维度为n, 粒子总群为num, 第i个粒子的位置表示为Xi=[xi1,xi2,…,xin], 速度向量表示为Vi=[vi1,vi2,…,vin], 粒子经过的最好位置记为Pibest=[pi1,pi2,…,pin], 在群体中所有粒子经过的最好位置的索引为Pgbest=[pg1,pg2,…,pgn]。 PSO算法的寻优是每个粒子在迭代过程中对其速度和位置进行更新:

Vi(k+1)=wVi(k)+c1r1[pibest-xi(k)]+

c2r2[pgbest-xi(k)],

(1)

Xi(k)=Xi(k)+βVi(k)。

(2)

其中,k为进化代数;w为惯性权系数;c1、c2为学习因子;r1、r2为[0,1]间的随机数。为了防止在迭代过程中粒子运动范围过大或速度太快,还需要设置参数对粒子的位置和速度进行更新并加以限制[9-10]。

PSO算法在寻优的早期普遍呈现出收敛速度快,且所有的粒子都往最优的位置靠拢,导致粒子趋于统一化,使得寻优的后期收敛速度变慢。因此引入了GA算法中的交叉和变异操作,结合了GA算法的全局寻优的特点,提高粒子在局部区域的收敛速度,以增强粒子搜索能力,实现两种算法的互补。

先对粒子进行交叉操作,按照一定的概率Pc进行交叉, 对于配对Xi、Xj的粒子,其位置、速度交叉过程分别为

(3)

(4)

式中:α1、α2为[0,1]间的随机数。

位置、 速度交叉操作后再对粒子以一定概率Pm进行变异得到的新个体:

(5)

f(g)=r2(1-k/Gmax)。

(6)

其中,Xmax和Xmin分别是粒子Xij取值的上下界,Gmax为最大进化代数。

2 GA-PSO优化BP神经网络过程

由于BP神经网络的权值通常用梯度下降法来确定[11],往往经过多次反复试验却很难找到最优的权值,存在着收敛速度慢、网络性能较弱、不能保证收敛到全局最优值等缺陷[12]。另一方面,BP神经网络的学习过程可以表述为网络参数优化的过程,其目的是最小化BP神经网络对学习样本的误差。因此本文采用GA-PSO算法优化BP神经网络的过程来代替BP神经网络学习的过程,以最小化学习样本的误差,优化BP神经网络的连接权值和阈值,达到提高网络模型的性能。GA-PSO优化BP网络的具体步骤为:

①设置BP神经网络各个层的神经元个数,得到D=(I+1)J+(J+1)P个参数[13], 其中I、J、P分别为输入层、隐含层、输出层的神经元个数,并设置神经网络连接权值和阈值的取值范围。

②粒子群初始化。将所有的参数表示为D维向量,作为粒子群个体的编码信息,神经网络和种群的个体之间形成了一一对应的关系,避免了编码/解码的过程。为了评价种群中粒子的质量,本文在训练神经网络中,通过实际输出与期望值的均方误差之和来构建粒子的适应度值函数:

(7)

其中,oi为训练样本的网络输出值;di为相应的期望值;N为集合大小。

③粒子群的迭代。按照式(1)、 (2)更新粒子的速度和位置信息, 再根据式(7)更新粒子的适应度,得到新的种群pop1。

④粒子群的遗传操作。 对新种群pop1中的粒子以交叉概率Pc进行两两交叉操作, 并对部分适应度值较差的粒子以变异概率Pm进行随机初始化。

⑤更新每个粒子的最好适应度值与最优位置Pibest,然后更新全局粒子的最好适应度和最优位置Pgbest,并代替上一次粒子遗传进化中最优的粒子。

⑥判断粒子群迭代次数是否到达最大迭代数, 或者粒子群的最好适应度值E是否达到设定的目标精度ε。 若是,则迭代终止, 以粒子群最好的位置作为BP神经网络的系统参数; 否则, 转至步骤③进行迭代。

GA-PSO混合优化BP神经网络的具体步骤如图1所示。

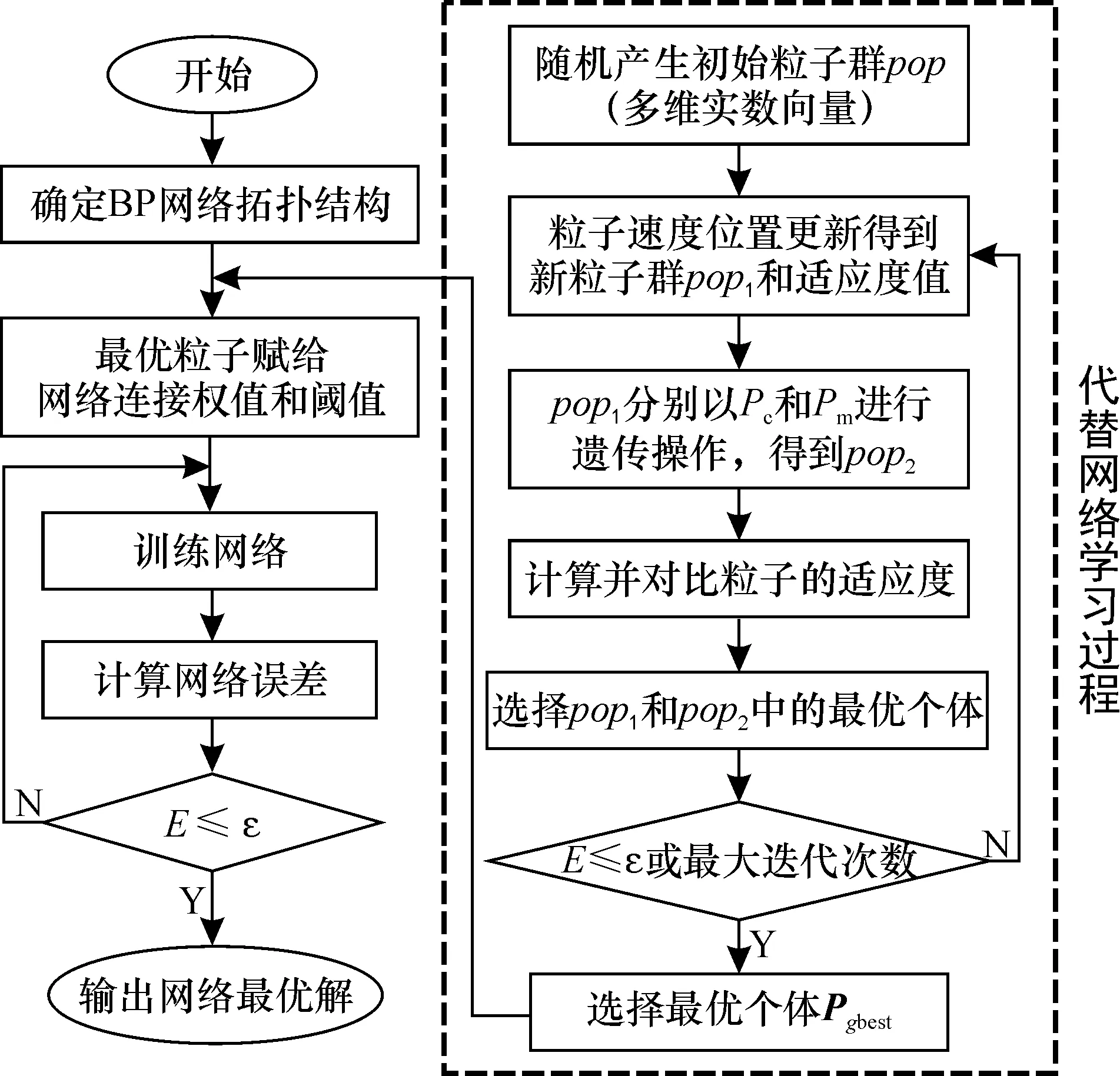
图1 基于GA-PSO混合优化BP神经网络Fig.1 Hybrid optimization BP neural network based on GA-PSO

3 实验验证

实验数据来自某钢筋混凝土重力坝8#观测点沿河流流向水平位移测量数据,其观测时间为2002年1月—2007年10月,观测周期为1个月,共70期样本数据。该观测点沿河流流向水平位移测量数据连同上游水位、周围环境温度等由大坝自动化监测数据库导出,大坝水平位移受多因素影响,其中上游水位最低值在2004年1月11日,为707.97 m,当日的坝址温度为9 ℃,水平位移自动监测值为1 mm;最高值出现在2006年6月12日,为754.47 m,当日的坝址温度为22.3 ℃,水平位移监测值为0.8 mm。相较于前后一期的大坝水平位移自动监测值,均受到了当日的坝址温度和上游水位的影响。因此，大坝8#观测点水平位移自动监测值呈现明显的非线性特征,具有代表性(图2)。

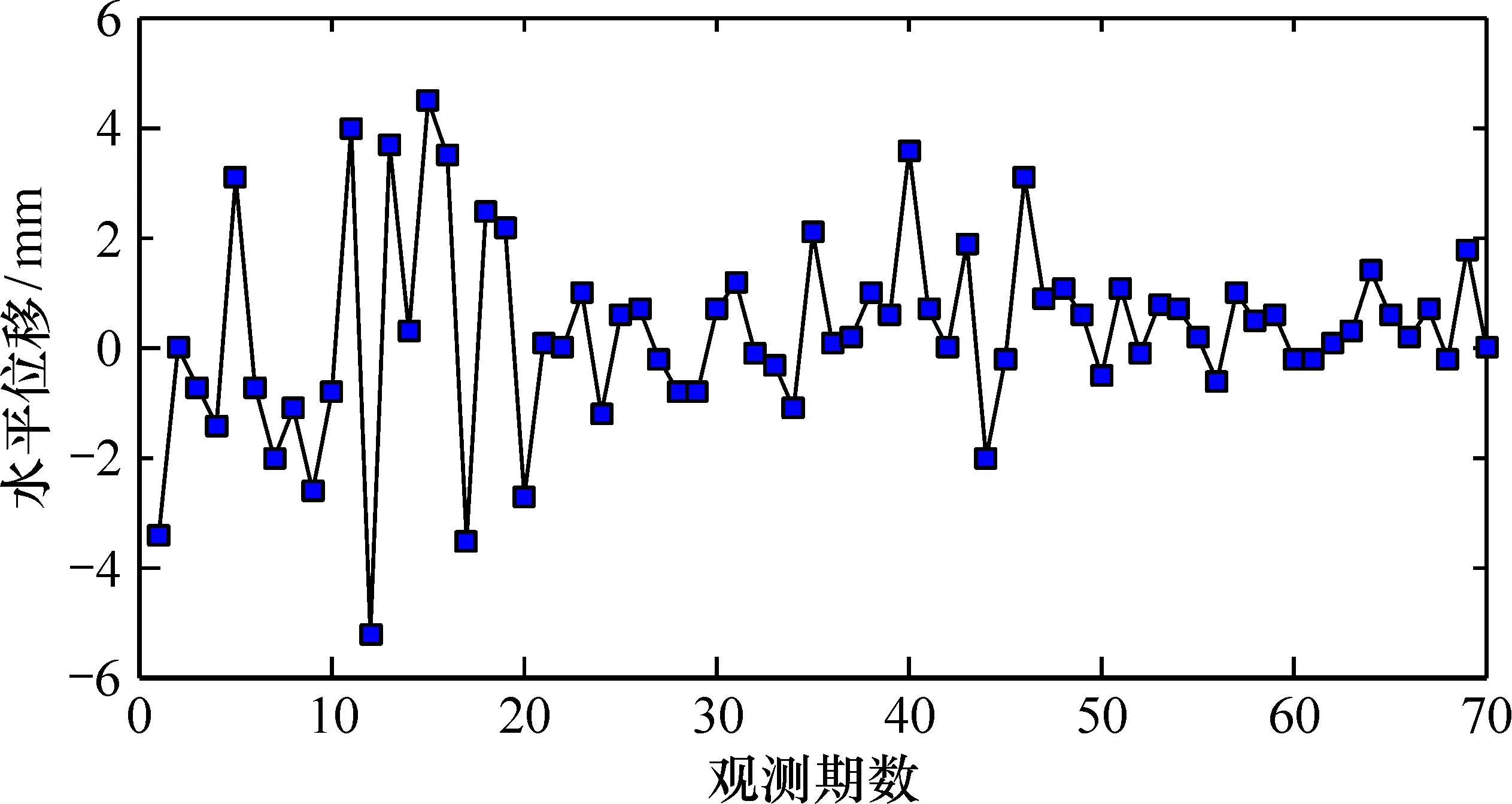
图2 8#观测点水平位移自动化监测曲线Fig.2 Automatic monitoring curves of horizontal displacement at rnonitoring Point 8

大坝水平位移自动化监测值存在多处突变值,在第12期大坝水平位移自动监测值为-5.2 mm,上游水位为741.31 m,坝址温度是总样本中的最低温度,为3.5 ℃,综合温度、水位等因素的影响,8#观测点在第12期出现了水平位移突变。总体看来,大坝8#观测点的水平位移变化呈现出非线性和非平稳的性质。为验证本文模型的有效性和优越性,以上述数据作为实验数据,利用本文模型优化网络的连接权值和阈值实现大坝变形预测,实验中采用BP模型、GA-BP模型、PSO-BP模型和GA-PSO-BP模型对相同的数据进行预测,从收敛速度、最优个体适应度值以及变形预测精度等方面对本文模型与其他模型进行综合比较。

3.1 最优粒子适应度值

本文算法通过训练神经网络的预测输出值与预期输出值的均方误差之和作为粒子适应度值,计算粒子每次迭代的个体适应度值,均方误差之和越小,适应度值越小,说明BP神经网络的系统误差越小。GA-PSO-BP、PSO-BP和GA-BP模型均采用相同的参数,其中，种群规模为20,最大进化次数为100,交叉概率Pc为0.95,变异概率Pm为0.1,惯性权重w为0.8,学习因子均为1.494 45,限制粒子的位置和速度分别为±5和±1,约束因子为0.2,神经网络设置收敛精度E=0.001时训练终止。

从各模型适应度值曲线图3中可以看出,本文模型充分发挥PSO算法收敛速度快的特点及GA算法良好的全局优化性能,能够在第3次迭代进化中获得最优个体适应度值;而由于GA-BP与PSO-BP模型自身存在一定的局限性,前者在寻找到最优适应度值时,产生收敛停止的现象;后者则是在前期的寻优过程中陷入了局部极值,导致其适应度值曲线呈多阶梯的形状。因此,本文模型相比于GA-BP和PSO-BP模型获得了较好的适应度值。从最终的适应度数值上分析,GA-PSO-BP模型为0.089 6,GA-BP模型为0.105 7,PSO-BP模型得到的最优个体适应度值为0.114 3,也体现了本文算法的优越性。由此可见,本文模型的训练网络的收敛速度显著提高,最优个体适应度值较低,说明本文模型获得较低的BP神经网络系统误差,以此达到优化BP神经网络的连接权值和阈值的目的。

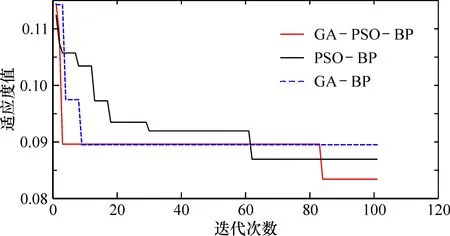
图3 各模型适应度值曲线Fig.3 Fitness curves of each model

3.2 大坝变形预测

实验中, 模型的输入因子是上游水位和坝址温度两个影响因子, 输出因子是大坝位移预测值, 每个模型使用相同的训练样本和测试数据集, 并对输入数据进行归一化处理, 设置相同的模型参数[14]。 实验时输入层神经元个数为2, 输出层神经元个数为1, 通过经验公式计算隐含层神经元个数:

Jc=(0.43mn+12n2+2.54m+0.77n+0.35)1/2+0.5,

(8)

其中:Jc为隐含层的神经元个数;m和n分别是输入层和输出层的神经元个数, 计算结果向上取整。经计算得知隐含层节点数应设置为3。经过多次试验对比, BP神经网络的学习率和动量系数均设为0.01, 训练样本数量设为1 000。

以1～50期上游水位和温度作为模型输入,对应的原始水平位移监测值作为模型的输出,输入51～70期的水位与温度影响因子,经模型计算即可得到对应的水平位移预测值。为了能够进一步提高模型预测效果,采用多步预测策略:以预测步长4为例,首先采用1～50期观测数据作为输入数据预测第51～54期的变形;然后采用第4～54期测数据作为输入数据预测55～58期,以此类推直至预测到70期,并与BP神经网络、GA-BP模型、PSO-BP模型进行对比分析;最后将预测值与大坝水平位移自动化监测值进行对比求差,根据两者之间的残差值分析得到用于本文实验的4种模型的精度。

本文以预测步长4为例，由各模型的预测曲线图4可以看出，BP神经网络模型的预测值与原始监测数据差距较大,由于BP神经网络的权值通常用梯度下降法来确定,容易陷入局部最优解,因此在第62～67期预测出现了较大偏差。经过GA算法优化的BP神经网络,由于GA算法在接近最优解时出现了收敛缓慢或停止的现象,虽然在前两期得到较好的预测值,但同样在第67期出现了较大的偏差。

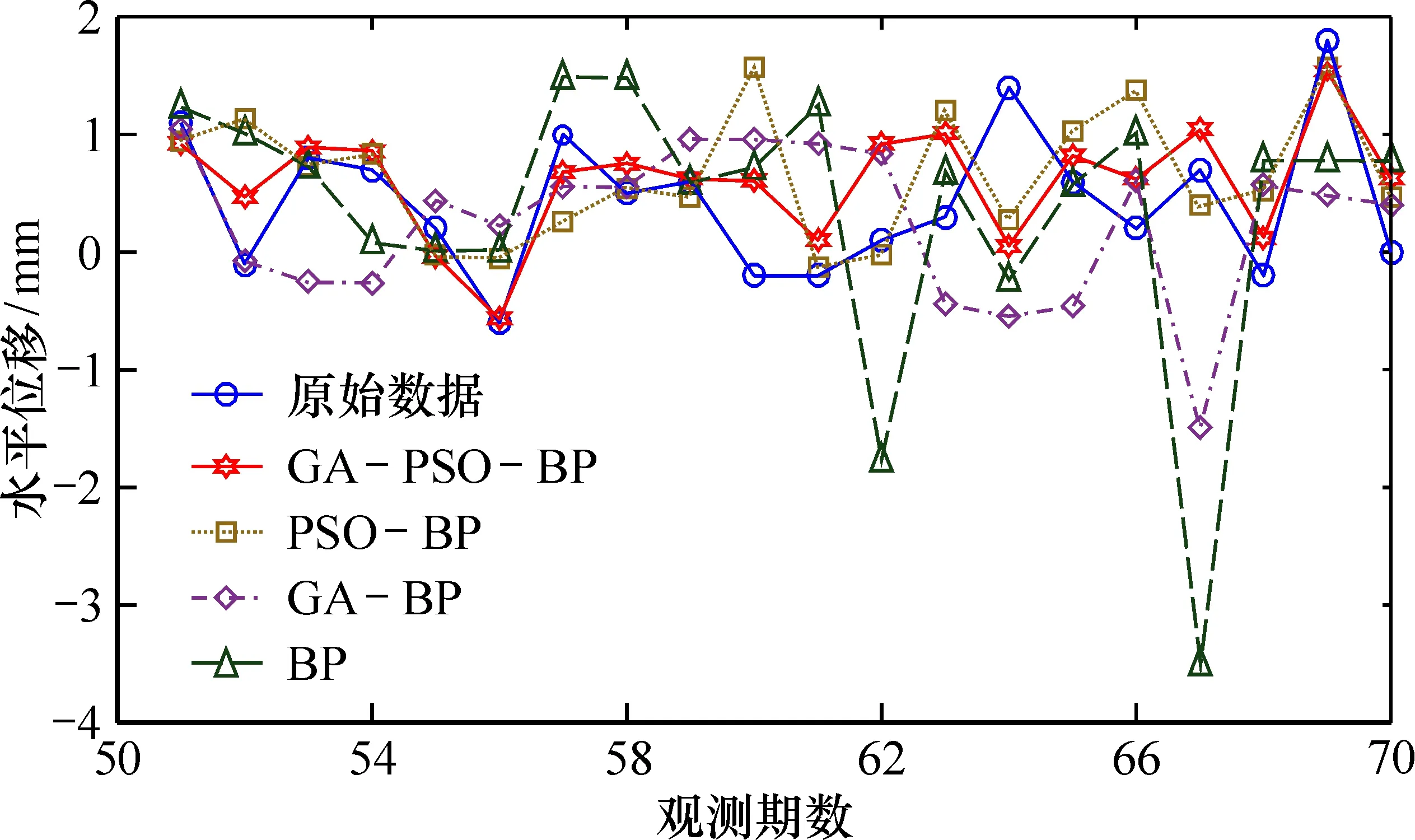
图4 模型预测值与大坝实际变形值对比Fig.4 Comparison between predicted values of various models and actual deformation values of dams

从图5残差图中,经过PSO算法优化的BP神经网络,预测的整体残差变小,提升了性能,但PSO-BP算法存在易陷入极值的缺陷,在第60期预测值与实际值有较大的偏差。

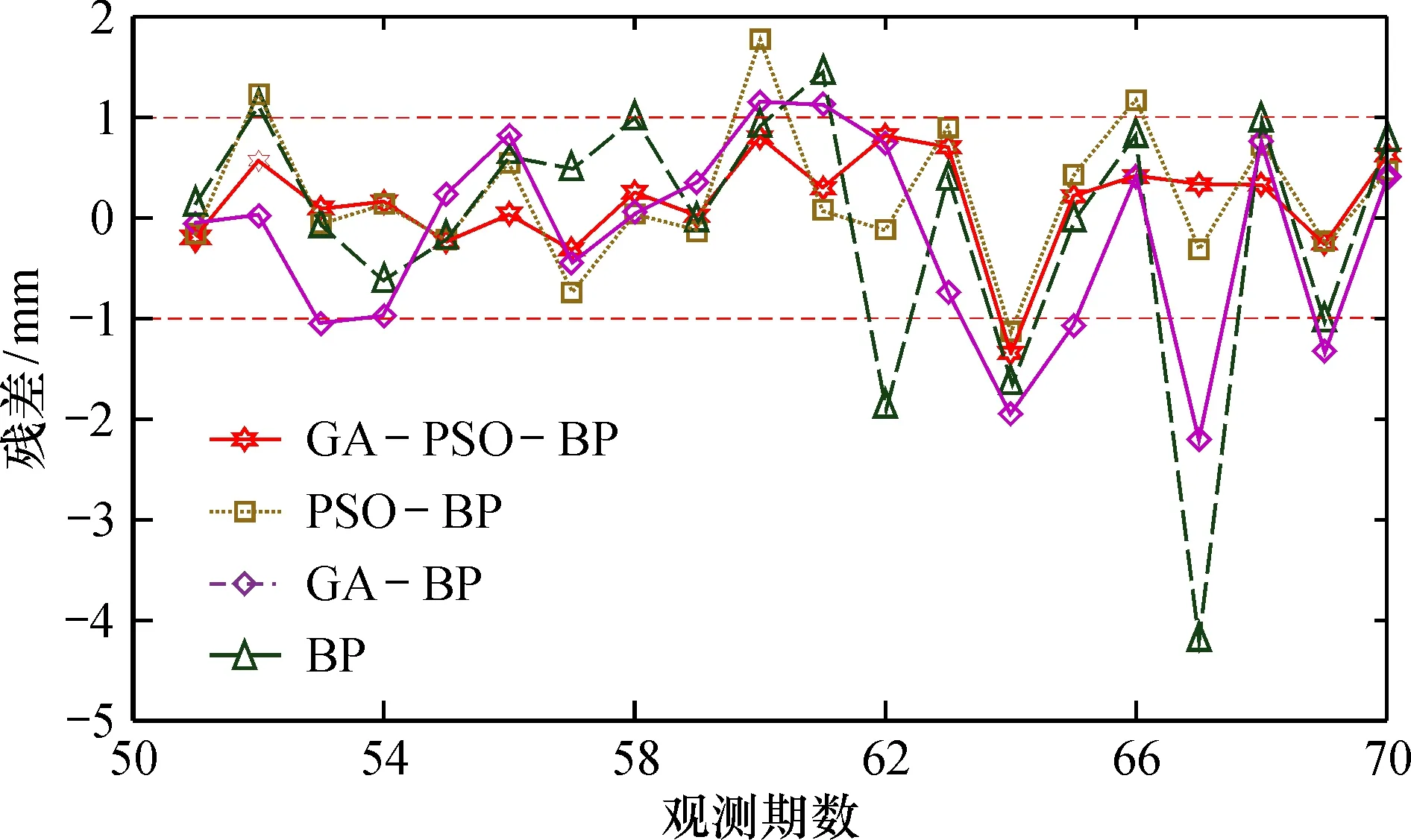
图5 预测模型残差值Fig.5 Residuals of prediction model

综合GA-PSO-BP模型的预测曲线和残差值曲线可以看出,通过GA和PSO模型的优势互补,预测值与实际值能够较好地吻合。

对实验结果的分析表明,本文提出的GA-PSO-BP模型适用于非线性变形序列的分析与处理,能够有效地对大坝变形进行预测,并达到较好的精度。此外，选择预测步长7和10对本文模型作进一步验证。同样地,在预测步长为7、10的实验中,GA-PSO-BP模型也取得了较好的预测效果。这些实验表明了GA-PSO-BP模型能较好地反映大坝水平位移的变化规律,通过构建多步预测模型,使得模型的网络性能得到提升,相较于其他3种模型取得了较好的预测效果,显著提高了BP神经网络预测结果的精度。为了进一步验证新算法的有效性,以平均绝对误差(MAE)和均方根误差 (RMSE)对各模型的预测精度进行评定[15]

(9)

(10)

其中,Yt为大坝水平位移自动化监测值;Yt′为各模型预测值;n是观测周期数;t表示大坝观测期数。各模型的预测精度见表1。

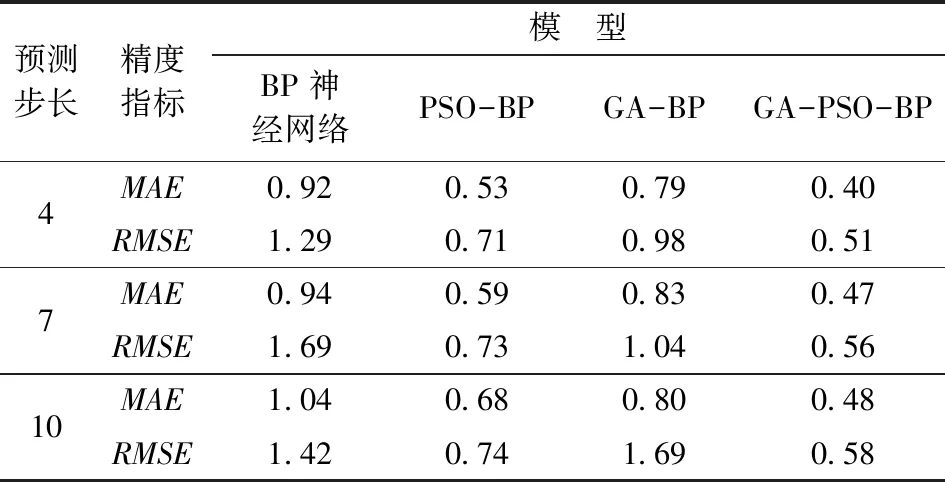
表1 各模型的预测精度Table 1 Prediction accuracy of each model mm

不同的预测步长,4种模型的预测精度都出现了不同程度的变化。BP神经网络的预测精度较低,不适用于长时间的多步预测。经过粒子群算法和遗传算法分别优化BP神经网络的连接权值和阈值,PSO-BP和GA-BP模型的预测精度也得到不同程度的提高,其中PSO-BP模型相较于GA-BP模型预测精度高。GA-BP模型预测步长7比预测步长10的平均绝对值误差大,不符合多步预测的规律,因此GA-BP模型对于多步预测方法的适用度较弱，GA-PSO-BP模型相比PSO-BP模型预测较为稳定且精度较高,误差增幅较小,更适合于进行多步变形预测。

综上所述,本文算法结合了GA、PSO算法的优点,优化了BP神经网络的连接权值和阈值,相较于BP、GA-BP、PSO-BP模型得到了较优的局部预测值,预测精度有所提高。因此,当大坝水平位移自动监测值呈现明显的非线性特征时,GA-PSO-BP算法能够取得较好的预测效果。

4 结 论

本文提出了一种基于GA-PSO混合优化BP神经网络的大坝变形预测方法,不仅解决了大坝变形数据中时间序列波动性与随机干扰项的问题,并且充分地结合了GA与PSO算法的优点,克服了BP模型的局限性,得到如下结论:

(1)将GA与PSO结合,以PSO算法为主,增加粒子的交叉和遗传操作,然后通过GA-PSO算法混合优化BP神经网络的连接权值和阈值,有效地改善了PSO算法粒子在寻优过程中容易陷入局部极小值和GA算法迭代时间长和收敛停止的缺陷,并且降低BP神经网络的系统误差,从而得到最优的神经网络连接权值和阈值。

(2)通过对实际工程的监测数据进行建模分析,针对大坝水平位移自动监测值呈非线性序列的特征,采用多步预测的方法,以不同的预测步长对大坝变形监测数据进行验证并分析。结果表明,本文模型提高了大坝变形预测的整体精度,保证了较优的局部预测值,并且对于多步预测方法具有较高的适应性。因此本文模型为大坝变形监测提供了一种新的选择方案,同时对滑坡、桥梁变形监测具有一定的参考价值。