渐开线圆柱齿轮齿根弯曲应力精确计算
姚和川,王明明,李 鸣,孙淑霞
(1.沈阳新松机器人自动化股份有限公司 激光事业部,辽宁 沈阳 110168;2.沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
0 引言
齿轮传动是机械传动中应用最广泛的一种形式,具有传动比准确、效率高、结构紧凑、工作可靠、寿命长等优点。齿轮最常见的失效形式为齿根弯曲疲劳应力引起的轮齿折断和齿面接触疲劳应力引起的齿面点蚀,而轮齿折断是最严重的失效形式,并且常常会突然发生,导致整台机器甚至是生产线停车、停产。因此在齿轮的设计过程中需要精确计算齿根的弯曲疲劳应力,而计算齿根弯曲疲劳应力的经典理论算法不仅需要进行大量的简化,还需要对计算结果进行修正[1-4]。本文采用ANSYS 软件建立齿轮齿廓曲线和齿根曲线,然后精确计算齿轮的齿根弯曲应力和齿面接触应力,并与理论方法的计算结果进行对比。
1 齿轮模型
1.1 渐开线齿廓曲线建模
如图1所示,当一条直线在圆周上作纯滚动时,直线上任意一点的轨迹称为该圆的渐开线,这个圆称为渐开线的基圆,其半径用rb表示;直线BK 称为渐开线的发生线;K 为渐开线上的任意一点,其向径用rK表示,渐开线AK 段的展角用θK表示;渐开线在K 点的压力角用αK表示。则渐开线的极坐标方程为:

将式(1)转化为直角坐标方程为:

其中


图1 渐开线的形成
1.2 齿根过渡曲线的建模
尽管过渡曲线在齿轮工作中不参与啮合,但是它却对齿轮根部的弯曲应力有着重要的影响,精确地绘制齿轮根部过渡曲线是进行齿轮根部弯曲应力有限元分析的先决条件。齿根过渡曲线形状取决于两个因素:一是刀具与齿坯的相对运动关系(加工方法);二是刀具顶部的刃形。齿轮加工方法不同或采用刀具不同,加工出的齿根过渡曲线则不相同。即使采用同一种加工方法用同一类刀具加工,若切齿刀具的齿顶圆角半径不同,所得到的齿根过渡曲线也不相同[5,6]。
滚刀加工齿轮时,如果刀具齿廓的顶部具有两个圆角,则切出的齿根过渡曲线如图2所示,I、II两段为延伸渐开线的等距曲线,III段为齿轮的根圆圆弧。
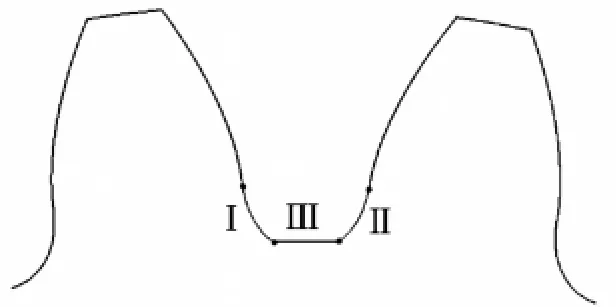
图2 第一类齿根过渡曲线
图3为双圆角刀具的基准齿形,其参数的关系式为:

其中:a 为刀具圆角中心到中线的距离;h*a为齿顶高系数;m 为模数;c*为顶隙系数;α 为压力角;b为刀具圆角部分的高度;r0为刀具齿顶的圆角半径。

图3 双圆角刀具的基准齿形
该过渡曲线的参数方程式为:
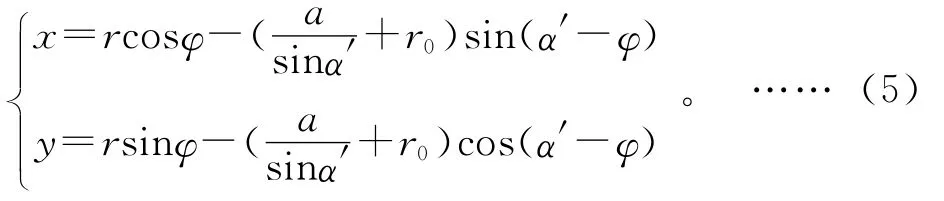

1.3 齿轮有限元模型
用上述方法建立的一对相啮合齿轮的有限元模型如图4所示,其参数为:模数m=4 mm,压力角α=20°,小齿轮齿数Z1=21,大齿轮齿数Z2=45,齿宽h=25mm,扭矩T=4 988N·mm。

图4 啮合齿轮的有限元网格模型
2 计算结果及分析
图5为两个齿轮的接触状态。此时两齿轮在节点处啮合,啮合点随齿轮转动发生变化。计算发现:在小齿轮转过0°~1.7°时第一对齿啮合,在14.25°~17.14°为第二对齿啮合,在1.7°~14.25°为两对齿同时啮合,小齿轮转角1.7°为单齿啮合的极限位置,此时齿根弯曲应力达到最大值,图6为齿根部位应力分布图。

图5 两齿轮的接触状态

图6 齿根部位应力分布
齿根弯曲应力的经典理论公式为:

其中:U 为载荷系数,取U=1;d1为小齿轮的分度圆直径,d1=84mm;YFa、YSa、Yε分别为齿形系数、应力修正系数和重合度系数,由参考文献[5]查图得到YFa=2.8,YSa=1.56,Yε=0.69。将已知参数代入式(7)计算得σF=89.1 MPa。
可见,理论方法的计算结果在修正前(修正前为29.7 MPa)与有限元计算结果(67.649 MPa)相差甚远,修正后的值(89.1 MPa)略大于有限元计算结果。两者的差异主要是理论方法在计算齿根应力时做出如下简化:①把渐开线齿廓简化为等截面梁;②对加载点和危险截面位置进行了简化;③忽略了由载荷Fn的水平分量Fncosα产生的剪应力和垂直分量Fnsinα 所产生的压应力,只按齿根危险截面的弯曲应力进行计算;④修正系数本身没有理论依据,存在较大的近似性。
3 结论
利用有限元软件可以精确建立渐开线和齿根曲线的真实形状,用接触单元可以计算出单齿啮合区和多齿啮合区。计算齿轮在单齿啮合区的极限位置啮合时齿根的应力分布,得到周期性最大弯曲疲劳应力。理论方法的计算结果在修正前与有限元计算结果相差甚远,修正后略大于有限元计算结果,两者的差异主要是由于理论方法的计算简化引起的。
[1] 武志斐,王铁,张瑞亮.18Cr2Ni4WA 齿轮弯曲疲劳试验及基于可靠度的试验数据统计研究[J].机械强度,2012(1):154-158.
[2] 林腾蛟,沈亮,赵俊渝.风电增速箱输出级齿轮副疲劳寿命有限元分析[J].重庆大学学报,2012(1):1-6.
[3] 韩志武,吕尤,牛士超.仿生表面形态对齿轮弯曲疲劳性能的影响[J].吉林大学学报,2011(3):702-705.
[4] 何晓华,陈兵奎.齿条型刀具对齿轮弯曲疲劳强度的影响分析[J].机械传动,2011(7):58-61.
[5] 吴继泽,王统.齿根过渡曲线与齿根应力[M].北京:国防工业出版社,1989.
[6] 杨庆详,赵言辉.渗碳及渗碳喷丸齿轮轮齿弯曲疲劳极限的定量分析[J].机械工程学报,2004,36(8):39-42.

