毛细管内径大小对测量水的黏滞系数的影响

徐昊成，周风琴

（辽宁师范大学物理系，辽宁大连 116029）

流体力学是一门实用性很强、适用性很广的学科。作为流体力学的一种应用，长期以来人们进行了大量关于流体黏滞系数测量的实验和研究。人们设计了多种实验方法来测量液体的黏滞系数，如落球法、毛细管法［1－3］、旋转圆筒法［4］、平动法、振动法［5］和光干涉法［6－7］等。其中毛细管法是最常用的方法之一。但用毛细管测量，在不破坏层流情况下，作者发现毛细管内径的大小对测量结果有较大影响。鉴于此，本文中用内径不同的毛细管测量了水的黏滞系数的对比实验，旨在找出毛细管内径大小与黏滞系数测量结果间的某些规律。

1 实验原理

当液体在运动时，不同液体层之间的速度是不同的。从图1 可以清楚看到液体在毛细管内的流动情况。

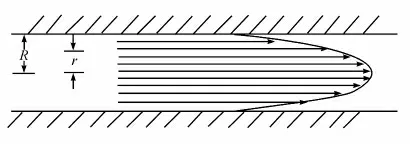
图1 液体在毛细管内流动

在相邻两层之间因有相对运动产生切向力，快的一层给慢的一层以拉力，慢的一层给快的一层以阻力，这对力称为内摩擦力或黏滞阻力［8－9］。液体内部相邻两层液体之间的内摩擦力f，除了正比于两层之间的接解面积S 之外，还正比于该处的速度梯度dv／dr，因此有

这就是决定液体内摩擦力大小的黏滞定律。式中比例系数η称为黏滞系数，它是描述液体黏滞性质的物理量，表征液体反抗形变的能力，在数值上等于当梯度变化一个单位时，作用于流体单位面积上的内摩擦力。

如果液体在层流的情况下流过一均匀细管时，根据泊肃叶公式有

dV 为dt时间内流过的液体的体积，（p1－p2）为毛细管两端压强差，r和l分别毛细管的半径和长度［10－11］。

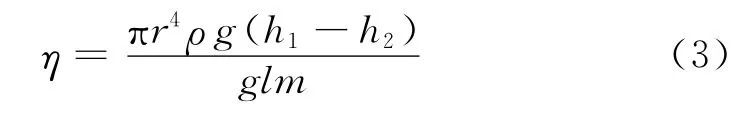
式中m 为单位时间内流过毛细管的液体的质量，ρ为液体密度，g 为重力加速度。

2 毛细管法测量水的黏滞系数的实验装置及方法

2.1 实验装置

图2为测量水的黏滞系数的实验装置。为了保持毛细管两端压强差（p1－p2）恒定，毛细管一端连通一恒水位槽。水槽中一部分水从毛细管流出，多余的水从水槽中间的溢流管排掉。这样，恒水位槽的水位始终保持一定，从而可维持毛细管两端稳定的压强差。

图2 测量水的黏滞系数的实验装置

2.2 实验步骤及方法

将图2装置连接调整后，用质量为m1的烧杯接从毛细管口流出来的水，每次3min，即t＝3min，分别测出流出水的质量（m2－m1）、压强计水位差（h1－h2）、水温θ及r、l、ρ。m＝（m2－m1）／3，由（3）式计算水的黏滞系数。

2.3 在实验中应注意事项

（1）保持水流稳定，排尽管中气泡。

（2）要调整恒水位槽位置，以保持毛细管中的水流为层流。

（3）测量时应经常观察恒水位槽中间的溢流管是否有水流，压强计水位是否稳定。

3 实验数据及结果

实验中实验使用的毛细管内径（直径）d 分别为:0.753、0.902、1.365、1.543mm，接水时间为t＝180s所得实验数据见表1—表4。表中η标为标准值。

表1 毛细管内径d＝1.534mm、毛细管长l＝785.0mm 时的实验数据

表2 毛细管内径d＝1.365mm、l＝801.0mm 时的实验数据

表3 毛细管内径d＝0.902mm、l＝778.4mm 时的实验数据

表4 毛细管内径d＝0.753mm、l＝795.0mm 时的实验数据

4 结果分析

从测试结果可知，水的黏滞系数的测量结果与实验装置中毛细管内径的大小有一定关系，随着毛细管内径不断增大，测试结果越来越接近相应温度下的标准值，也就是说在一定范围内毛细管内径越大，测量结越准确，产生的误差越小。这主要有以下几个原因:

（1）因（3）式中有r4项，通过误差传递，毛细管内径的测量误差会给最后结果带来最大影响。

（2）毛细管的制造是一项比较精密的技术，毛细管在拉制过程中有一定锥度，这就造成了毛细管本身的不均匀性，而且有时毛细管的截面并非是正圆。在实验室条件下，一般只能用读数显微镜对毛细管的端口进行测量，这样就不可避免地造成内径的测量误差，毛细管越细，引入的相对误差就越大，对水的黏滞系数的测量结果影响也就越大。

（3）由于技术条件限制，通常拉制的毛细管并不能保证内壁的绝对光滑，或有凸凹，这样水流受到影响，同样管子越细影响越大。另外还有一个重要原因是，当管子内径越小时，单位时间内流出水的质量m越小（如第4个毛细管水流量m≈0.01g／s）如此少量的水在实验过程中除了被蒸发掉一部分，在称质量时，同样地相对误差也就越大。因此用这样细的毛细管测得的结果，势必造成较大误差。

为了得到较好的测量结果，应避免使用1 mm 以下内径的管子，从本实验的测试结果，使用1.5mm 实验结果较为理想。

为了减小测量误差，除了上述的尽量避免使用内径太小的管子外，条件允许还可以用比较法测量，比较法可以从公式中消掉r4的影响，从而使测量结果的精确度大大提高。

5 关于层流与雷诺数

黏性流体运动有两种形态，即层流和湍流（紊流）。层流是指流体作有规则的层状或流束状的运动，各部分分层流动、互不掺混，流体质点互不干扰地前进，质点的轨迹是光滑的，而且流场稳定。湍流（紊流）的特征是流体运动极不规则，各部分激烈掺混，流体质点交错而又混乱地向前运动，质点除了主要的横向运动之外，还有附加的纵向运动存在，而且流场极不稳定。泊肃叶公式只能适用于层流。

判断流体运动状态的重要参数是雷诺数。雷诺数是指所研究区域内特征的惯性力和特征的黏滞力之比。定义式为

其中，v是流体的特征速度，L 是流动的特征长度，ρ是流体的密度，η是流体的黏滞系数。

对于圆管，雷诺数可表示为

实验证明，对于不同的黏滞系数的流体，在不同直径d、保持几何形状相似的管道中，以不同的速度v 流动时，只要他们的雷诺数Re相等，则流动状态必然相同。因此，雷诺数可作为判别液体流动状态的普遍标准。

通过对实验数据进行分析计算，得到各个毛细管每次实验的雷诺数Re都远远小于下临界雷诺数（2 000～2 300），从而保证了适用于公式的基本实验条件。

（

）

［1］何圣静.物理实验手册［M］.北京:机械工业出版社，1989.

［2］杨述武.普通物理实验:力学、热学部分［M］.北京:高等教育出版社，1983.

［3］北京大学物理系普通物理教研室.普通物理学:力学部分［M］.北京:人民教育出版社，1978.

［4］林佩芬，周炎辉，许定生，等.旋转圆筒法测粘滞系数的计算公式讨论［J］.物理与工程，1996（4）:23－25.

［5］胡德旺.旋转球体法测粘滞系数的方法研究［J］.实验技术与管理，2006，23（1）:30－31.

［6］窦会庆，徐建波.一种利用光致旋转效应测量液体粘滞系数的新方法［J］.山东师范大学学报:自然科学版，2009（1）:58－60.

［7］徐建峰，李胜荣，周静，等.用布里渊散射测量水的粘滞系数［J］.光学学报，2001，21（9）:1113－1115.

［8］李富成.流体力学及流体机械［M］.北京:冶金工业出版社，1980.

［9］张捷迁，章光华，陈允文.真实流体力学［M］.北京:清华大学出版社，1986.

［10］张立.大学物理实验［M］.上海:上海交通大学出版社，1989.

［11］张存恕.大学物理实验［M］.成都:四川科学技术出版社，1986.

［12］Urone P P.College Physics［M］.Beijing:CHINA MACHINE PRESS，2002.