垄断者跨时利润和最优化模型与科斯猜想
余 敏 上海市普陀区业余大学
近几十年,博弈论不断加速向现代经济学渗透。罗纳德·科斯(ronald coase)提出一种观点,认为在某些条件下,经济的外部性或曰非效率可以通过当事人的谈判而得到纠正。“科斯猜想”(Coase Conjecture)是科斯在1972年发表的《Durability and Monopoly》论文中所做的一个猜测。科斯教授提出,由于将来销售的耐用品将会影响到现在所售出的产品的未来价值,在垄断耐用品生产者没有对未来的产量水平做出承诺时,如果消费者具有价格下跌的理性预期,那么垄断价格就会迅速降到边际成本水平。这个观点源于一系列案例,科斯本人一直拒绝把他初始论文中的论点加以广泛地推广,因此对于他论文中的每一个解释,出现另外多种似乎说得通的看法。以下通过讨论垄断者跨时利润和最优化模型进行提示性证明。
一、垄断者的跨时利润
假设1 单位生产成本为0,(此假设只是为了讨论的方便)。
假设2 垄断者和消费者无限地活着。
假设3 消费者的估价ν 均匀地分布在[0,1/(1-δ)]上。(相当于每阶段估价均匀地分布在[0,1]上)
假设4 估价为ν 的消费者效用δt(ν-Pt),Pt表示t
假设5 “稳态假设”:当某一时间面对价格P时,任何估价超过ω(P)=λ P的消费者将购买,估价较低的消费者不会购买,其中λ>1。反之,如果在某一时间估价超过ν 的消费者买了,而其他的消费者没有购买,垄断者要价P(ν)=μν,其中μ<1
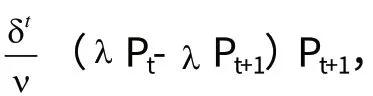
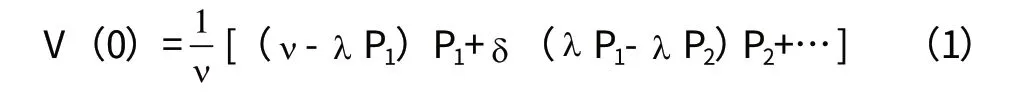
其中ν>λ P1>λ P2>…
引理1 证明垄断者对Pt的最优化导致一种线性规划,其中λ 作为μ 的函数由下式给 1-2 λμ+δ λ2μ2=0
[证明] 对(1)式中的P1求导令其为0,得
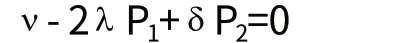
由于 P1=μν,P2=μ(λ P1)= λ μ2ν,即得
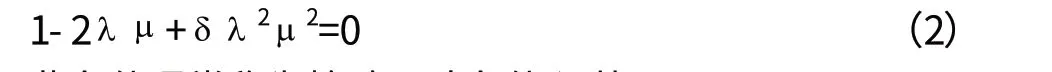
此条件通常称为检验二阶条件 证毕
引理2 消费者ω(P)的无差异方程

[证明] 估价为λ P的买方现在就买和等待下一个阶段买之间是无差异的,即
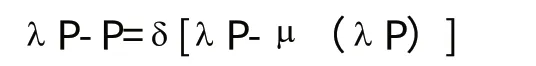
两端去掉P即得(3) 证毕
引理3 当δ →1时,垄断者的利润趋于0
[证明] 由(2)与(3)解得
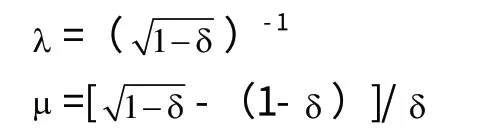
由此得1lim
δ→μ=0 证毕
此引理的实际意义为,当消费者的贴现函数接近于1时,则有充分大耐心来等待,以使得消费者支付获得最大,这样就迫使垄断者以边际成本来定价,从而利润趋于0。
假设7 垄断者承诺价格顺序(P1,P2,P3,…)
引理4 证明在寻找最优价格政策时,垄断者约束自己于价格序列(单调减少)P1≥ P2≥ P3≥…
[证明] 对某些正的K,价格Pt≥Pt-k将不被任何消费者接受,因为消费者会以低价Pt-k购买,并较早地享用该商品,因此,选择Pt=min
k(Pt-k)导致同样的结果。
二、最优化模型
由引理2.估价为ν 的消费者在接受Pt和等待Pt+1之间无差异
当且仅当 (ν-Pt)=δ(ν-Pt+1) 及(1)式,得
垄断者的最优化问题为:
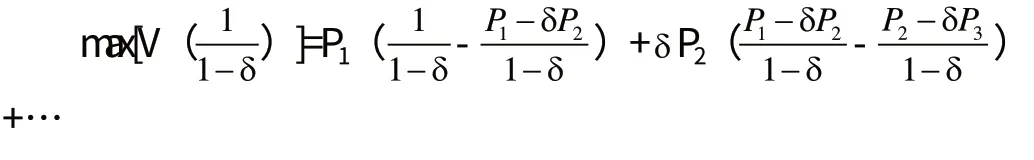
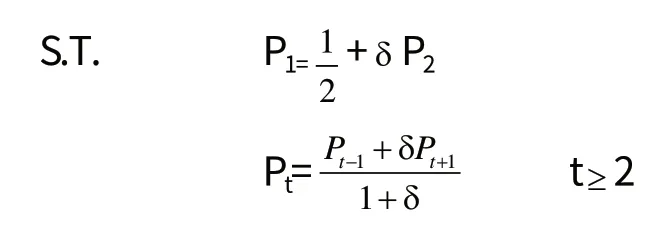


代入目标函数可得
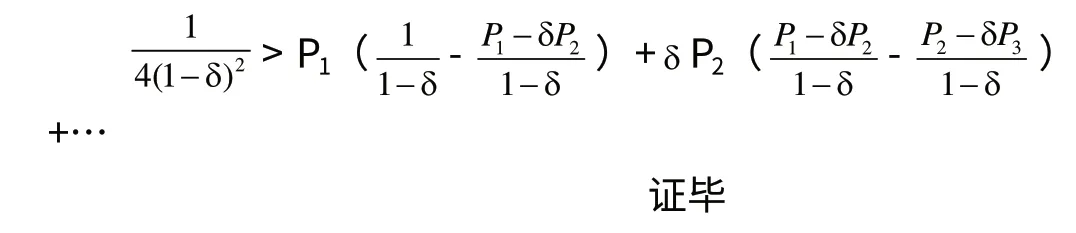
三、科斯猜想的提示性证明
科斯在耐用品和跨时价格歧视的极端情况下猜想:当价格调整的间隙收敛为零时,一个无限耐用品的生产者损失了他的全部垄断力量。
证明:考察无限时序t=1,2,…。对于垄断者的要价序列{P1,P2,……Pt-1},卖方在t期开始时的后验信念,是在[0,bt]区间估价为某一b的买方还没有购买商品,而在(bt,+∞)区间估价为b的买方已经以某一bt购买时的信念,即垄断者的后验信念一定要与他的裁剪的先验信念相一致。
假设买方遵从一种简单的“稳态的”策略:即在t期要价Pt时估价超过 β(Pt)的买方购买,而估价低于β(Pt)的买方不购买,其中β(·)是递增函数,且对所有的Pt>0,β(Pt)> Pt
为了简化起见,令C=O垄断者的边际成本,F(b)代表在[0,+∞]的买方估价的积累分布(对b>0,有F(0)=0,F(b)>0,F(+∞)=1)最后取贴现因子δ=exp(-γ·△),其中△是阶段之间的实际时长,γ>0,显然我们对△趋于0时所发发生的事情感兴趣。
由于买方策略的稳定性,垄断者自一给定期t开始的利润的当前贴现价值,取决于剩余买方的分布。令V(bt)代表贴现利润,显然V(·)是非递增函数,令Ft≡F(bt)代表t期前还没有购买的买方比例。
固定真实时间ε>0,令△收敛于0,对任意η>0,存在着一个充分小的△和t,使得(t+2)·△<ε,满足
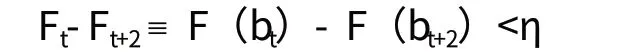
由于0-ε之间的阶段数趋于无穷,我们总能发现两个连续的阶段使得在这些阶段销售的总数是由一定数值限定的。
如果从真实时间ε起的利润V(bε/Δ)是不可忽略的,垄断者就会有积极性通过快一点削价加速此过程,因此,来自歧视的收益是二阶的,而通过在t期作出计划在t+1期作出的提供,垄断者会通过一个阶段加速此过程,并且获得一阶收益(对△),如果V(bε/Δ)不是很小的话
下面写出垄断者宁可在t期要价Pt,在t+1期要价Pt+1而不是直接在t期要价Pt+1,情况下的条件:

根据bt+1定义,估价bt+1的买方在接受Pt和接受Pt+1之间是不在意的,因此

即Pt-δPt+1=(1-δ)bt+1
代入(1),并用(1-δ)除,得

还有Ft+1> Ft+2,因此(4)式可写成
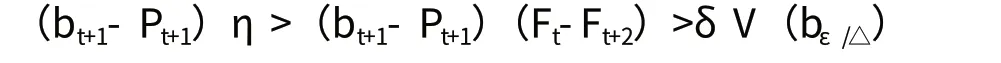
这意味着通过选择充分小的η,能够使卖方自真实时间起的贴现利润值任意小,因此通过选择足够小的△,使自任何时间(包括趋近于0的时间)起的贴现利润值任意小。
科斯定理是现代产权经济学关于产权安排、交易费用与资源配置之间关系的思想的集中体现,也是现代产权经济学的基本核心内容,全面、准确地把握科斯定理的含义,对于深化我国国有企业改革,建立现代企业制度具有一定的借鉴意义。
[1]张维迎.《博弈论与信息经济学》.上海人民出版社
[2][美] Drew.Fudenberg,[法]Jean.Tirole.《博弈论》.中国人民出版社
[3][瑞典] W.W eibull.《演化博弈论》.上海三联书店、上海人民出版社,2006.3

