BP神经网络法预测水基绒囊钻井液当量静态密度
王金凤 杨 晨 毛邓添 苟斐斐
(中国石油大学石油工程教育部重点实验室,北京 102249)
水基绒囊钻井液是由成核剂、成膜剂、成层剂和定位剂按比例配制而成的钻井流体[1](郑力会,2011)。绒囊结构独特,非常适用于低压漏失地层钻完井使用[2](郑力会等,2010)。冀东油田修井[3](李良川等,2011)、煤层气直井钻井[4](王德桂,2011)、煤层气分支井钻井[5](孟尚志,2012)、煤层气水平井钻井[6](孙法佩,2012)等作业实践,都证明流体防漏堵漏效果良好。但井下作业时井下流体静态密度与地层压力是否为欠平衡状态,没有定量研究。
要证明是否为欠平衡状态,需要预测井下当量静态密度。Methven N E 等[7](1972)室内利用PVT实验数据预测井下条件钻井液密度的方法得到广泛认可。后来, Krook G W 等[8](1984)、Kutasov[9](1988)、Peters E J 等[10](1991)、Eirik Karstad 等[11](1998)利用PVT 实验数据给定函数形式,通过数学方法拟合函数系数建立预测模型的方法,使这种方法从定性走向定量,也得到一定程度的认可。
为此,王金凤等[12](2012)用多元回归法拟合了压力1~20 MPa、温度30~130 ℃的水基绒囊钻井液PVT 实验数据,并以井深为自变量,建立了绒囊钻井液静态当量密度预测模型。尽管提出用温度和压力相关的井深表征密度变化,使现场容易了解地下密度变化情况,但仍没能摆脱先给定公式形式再拟合公式系数的常规方法。这种方法,一旦公式形式不合适,拟合精度便会受到影响。不给定公式形式的BP 神经网络法,由于其反复训练降低误差的特性,能很好地满足拟合要求。因此,尝试通过以密度为0.85 g/cm3的绒囊钻井液PVT 实验数据为样本,建立密度—压力—温度的BP 神经网络。利用此网络,预测水基绒囊钻井液井下当量密度,对比多元回归方法预测结果,与室内及现场实测数据吻合度更高。
1 BP 神经网络预测模型建立
BP 神经网络是一种按误差逆传播算法训练的多层前馈人工神经网络[13](RUMELHART D E 等,1986)。用最速下降法训练模型,通过反向传播误差不断调整网络的权值和阈值,使网络的误差平方和最小,得到预测模型[14](MCCLELLAND J L 等,1988)。与多元回归模型相比,BP 神经网络拟合不需要给定公式形式和考虑自变量间的关系[15](FAHLMAN S E,1988),更兼有自适应、自组织和实时学习特点,可根据新获得的数据实时调整网络权值和阈值,适合实际工程中对未知区域探索的数据外推问题,预测结果精度高。因此,应该适用于井下密度预测。
1.1 BP 神经网络模型的建立
BP 神经网络,从拓扑结构上分为输入层、隐层和输出层等三层。
输入数据有钻井液温度T、钻井液所承受的压力p,输出数据有钻井液密度ρ。输出数据可用输入数据和激活函数表示,见式(1)。
以已有的绒囊钻井液PVT 实验数据为数据样本,利用Matlab 软件建立所需的BP 神经网络。
首先,用newff 函数建立三层BP 神经网络,形式如下

式中,PT 为压力与温度样本矩阵;10 和1 分别为隐含层和输出层神经元个数;tansig 和purlin 分别表示输入层和隐含层间及隐含层和输出层间的神经网络传输函数;trainlm 表示训练中采用Levenberg-Marquardt 算法调整权值和阈值。
然后,用train 函数训练网络NET=train(PT, rou)。网络中的rou 为钻井液密度样本矩阵。
最后,采用sim 函数运行训练好的网络rouout =sim(NET, PTin)。网络中的PTin 为输入压强和温度矩阵;rouout 为输出钻井液密度。至此,BP 神经网络建立完毕。
一般情况下,建立BP 神经网络需要一部分数据用于训练模型,另一部分数据用于测试模型,然后才能使用。与之对应,误差有训练误差和测试误差两种,一般采用均方差(MSE)及相关系数表征网络性能好坏。MSE 越小,相关系数越接近1,表示网络的可信度越高。验证数据均方差越低,网络性能越好。BP 神经网络预测密度为ρout,i(p, T),实验数据为ρri(p, T),则网络均方差见式(3)。
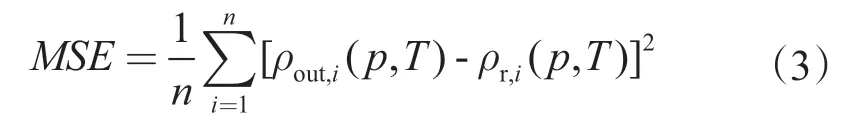
式中,i 为实验点计数;n 为实验点总数。
建立网络训练过程中,用蓝线代表训练数据组,绿线代表验证数据组,红线代表测试数据组的均方误差。迭代步数、均方差变化如图1 所示。

图1 BP 神经网络训练、测试及验证数据误差 随迭代步数变化
从图1 中可以看出,模型迭代到178 步时,验证数据组的均方差为5.7321×10-8(图中右下方绿色小圆圈中值),达到最小值且已满足预期要求。模型已最优。
以验证数据组的均方差最小为依据,建立模型后,需要实际对照训练数据、测试数据以及全体数据目标值与模型输出值的误差,才能确定模型是否合适。若输出值与目标值完全符合,则图2 中所有数据点应该分布在“目标值等于输出值”的直线(即图形对角线)上;符合程度越低,输出值与目标值差别越大,数据点则越偏离对角线,如图2 所示。
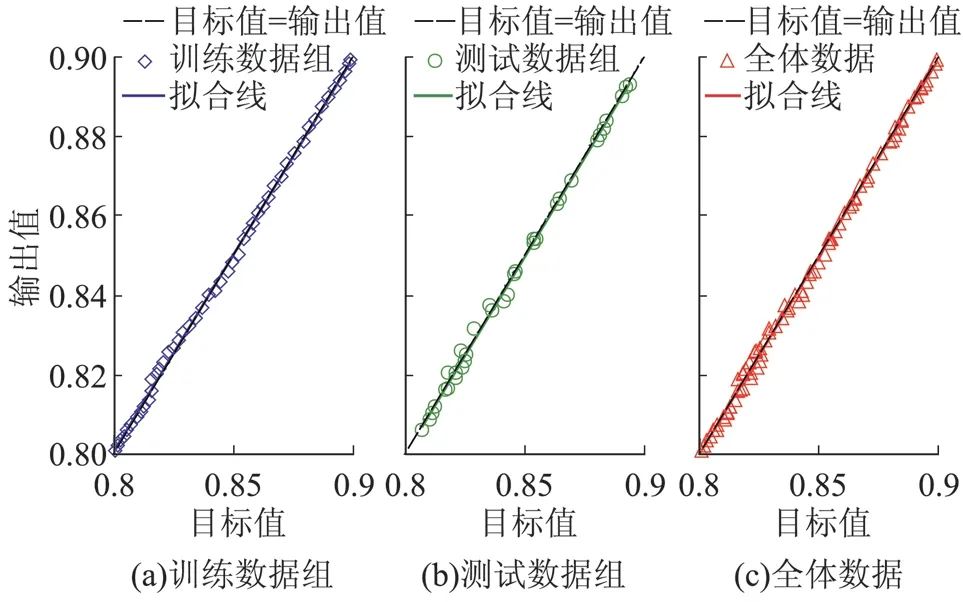
图2 BP 神经网络模型输出值与目标值误差对比
从图2 中可以看出,建立的神经网络模型,无论是训练数据组、测试数据组还是全体数据,模型输出值与目标值相差不大。输出值拟合线与对角线(目标值等于输出值的直线)相关系数较高,分别达到0.998 79,0.998 91 和0.998 83。说明利用BP 神经网络可以精确拟合实验数据,能够满足建立绒囊钻井液静态密度预测数学模型的要求。
1.2 钻井液静态密度预测模型的建立
钻井液在井下某深度处的压力等于其上部所有钻井液静液柱压力之和

式中,p 为钻井液压力,MPa;p0为大气压,MPa;ρ为钻井液静态当量密度,g/cm3;g 为重力加速度, m/s2;h 为井深,m。
式(4)两边,对h 微分,得到

将式(1)带入式(5),得
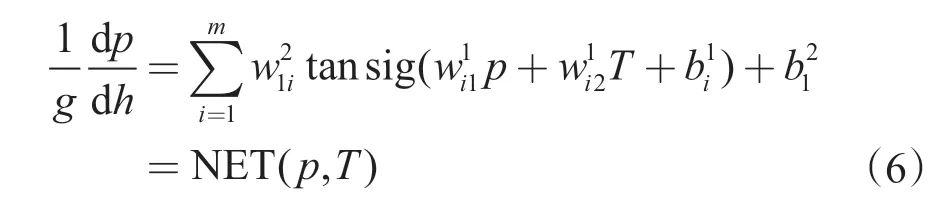
边界条件为

对式(7)进行一维显式差分计算,得

整理得到第d+1 个网格处的压力

式中,pd为第d 个网格处的压力,MPa;Td为第d 个网格处的温度,℃
可近似认为钻井液的温度T 等于地层温度。如果已知地温梯度a 和地表温度T0,则式(10)成立。

将所求得的p,T 值代入BP 神经网络模型,便可求得密度ρ(h)。
实验中测得绒囊钻井液在常温常压下密度为ρ0,现场所用钻井液密度通常与实验室略有差距。同一类钻井液,不可能逐一测试不同密度下的PVT 特性。现场钻井液密度可用实验室PVT实验数据修正。设现场使用的钻井液常温常压下密度为ρs,记修正系数α=ρs/ρ0,则修正预测密度ρ′(h)=αρ(h),即实际工作密度。至此,就可以用BP 神经网络模型预测井下密度。
2 BP 神经网络预测模型应用
应用建立的BP 神经网络模型预测井下密度,其每米密度变化需要通过迭代计算完成。目前大多采用Levenberg-Marquardt 算法。此法是最速梯度下降迭代法和高斯—牛顿迭代法的结合,与传统方法相比,迭代次数少,收敛速度快,精确度更高。每次迭代不是沿着单一的负梯度方向,而是允许误差沿着恶化的方向搜索,通过在最速梯度下降法和高斯—牛顿法之间自适应调整来优化网络权值,使网络能够有效收敛,大大提高了网络的收敛速度和泛化能力。
磨80-C1 井是在原井眼开窗侧钻的一口短半径水平井[16](胡永东等,2013)。目的层垂深2 728.00 m,地层温度为T=40.134+0.0091h。现场使用密度为1.02 g/cm3的碳酸钙加重绒囊钻井液钻井,固相含量7%。含固相的绒囊钻井液密度ρout,s可以用修正系数来计算

式中,ρout为无固相绒囊钻井液密度,g/cm3;ρs为固相碳酸钙的密度,g/cm3。
实际测量结果与PVT 实验实测数据结果、BP神经网络法预测结果以及传统多元回归法预测结果对比如图3 所示。

图3 2500 m 以浅现场实测密度与室内静态当量密度 预测值对比
从图3 可看出,从100 m 开始,4 条曲线显示井下绒囊钻井液密度均随井深增加而降低,其中BP 神经网络预测密度值与实测密度值最接近。计算表明,BP 神经网络预测密度值最大相对误差1.57%,多元回归预测密度值最大相对误差4.32%。可见,BP 神经网络模型预测井下密度更准确。
如果使用绒囊钻井液在该地区向更深处钻井,需要进一步预测2 500 m 以深绒囊钻井液密度变化趋势,推算绒囊是否存在,以估计是否还能有效封堵。BP 神经网络预测值与文献[12]多元回归预测值对比结果如图4 所示。

图4 两种不同数学方法得出2 500 m 以深绒囊钻井液 静态当量密度预测值对比
从图4 可以看出,2 500~6 000 m 范围内,两种方法预测结果均显示绒囊钻井液密度能够继续降低,并在6 000 m 仍保持一定密度,表明绒囊未在高温高压下被压缩成连续相,证明绒囊结构抗压缩能力强的同时也间接证明了井底条件下绒囊在高温高压下依然存在,能满足深井作业防漏堵漏要求。相比多元回归预测曲线,BP 神经网络预测曲线波动更小,数值更稳定,更适于现场工程应用。
3 结论及建议
利用BP 神经网络拟合绒囊钻井液压力—温度—密度关系,并以此为基础建立了绒囊钻井液井下静态当量密度预测模型。预测2 500~6 000 m 绒囊钻井液密度,发现绒囊钻井液密度随井深增加缓慢降低,与多元回归方法预测的规律一致。但是,与多元回归方法相比,BP 神经网络法预测精度更高。同时,BP 神经网络井下静态密度预测模型为井下钻井液密度预测以及其他井下流体密度预测提供了一种新方法。
[1] 郑力会.仿生绒囊钻井液煤层气钻井应用现状与发展前景[J].石油钻采工艺,2011,33(3):78-81.
[2] 郑力会,曹园,韩子轩.含绒囊结构的新型低密度钻井液[J].石油学报,2010,31(3):490-493.
[3] 李良川,卢淑芹,彭通,等.冀东油田绒囊修井液控制储层伤害应用研究[J].石油钻采工艺,2011,33(3)∶31-34.
[4] 王德桂,何玉云,卜渊,等.吉X 井煤层气水基绒囊钻井流体实践[J].石油钻采工艺,2011,33(5)∶93-95.
[5] 孟尚志,窦政辉,刘彬,等.FL-H2-L 煤层气五分支水平井绒囊钻井液技术[J].钻井液与完井液,2012,29(1):5-8.
[6] 孙法佩,张杰,李剑,等.煤层气215.9mm 井眼水平井水基绒囊钻井流体技术[J].中国煤层气,2012,9(2)∶18-21.
[7] METHVEN N E, BAUMMANN R. Performance of oil muds at high temperatures[R]. SPE 3743,1972.
[8] KROOK G W,BOYCE T D. Downhole density of heavy brines[R]. SPE 12490,1984
[9] KUTASOV I M. Empirical correlation determines down hole mud density[J]. Oil & Gas Journal, 1988,86(12)∶ 61-63.
[10] PETERS E J, CHEVENVER M E,ALHAMADAH A M. Oilmud∶a microcomputer program for predicting oil-based mud densities and static pressures[J]. SPE Drilling Engineering, 1991, 6(1)∶ 57-59.
[11] EIRIK KARSTAD,BERNT S. Aadnoy. Density behavior of drilling fluids during high pressure high temperature drilling operations[R]. SPE 47806, 1998.
[12] 王金凤,郑力会,韩子轩,等.用多元回归法预测水基绒囊钻井液当量静态密度[J].石油钻采工艺,2012,34(2):33-36.
[13] RUMELHART D E, MCCLELLAND J L. Parallel distributed processing∶ explorations in the microstructure of cognition [M]. London∶ The MIT Press, 1986.
[14] MCCLELLAND J L, RUMELHART D E. Explorations in parallel distributed processing∶ a handbook of models, programs, and exercises[M]. London∶ The MIT Press, 1988.
[15] FAHLMAN S E. An empirical study of learning speed in back-propagation networks[R].CMU-CS-88-162,1988.
[16] 胡永东,赵俊生,陈家明,等. 磨80-C1 侧钻水平井绒囊钻井液实践[J]. 钻采工艺,2013,36(1):110-113.

