基于椭圆度及壁厚参数的连续油管低周疲劳寿命预测
何春生 刘巨保 岳欠杯 李伟权
(1.中石油长城钻探工程公司,北京 100101;2.东北石油大学机械科学与工程学院,黑龙江大庆 163318)
0 引言
随着石油工业的不断发展,连续油管(Coiled Tubing,简称CT)作业设备广泛应用于油气田修井、钻井、完井、测井等作业,在油气田勘探开发技术上发挥着越来越重要的作用[1-3]。连续油管在作业过程中经受多次塑性弯曲变形[4-5],这些变形经过多次作业导致发生低周疲劳是连续管典型的失效模式。目前,国内外大多采用现场实验法、疲劳实验机、疲劳寿命模型等3 种方法对连续油管进行疲劳寿命预测[6-8],由于反复实验成本高、疲劳实验机自身的局限性及疲劳寿命模型经验系数多等特点,使预测寿命值与实际寿命仍存在较大误差,而且国内外文献大多采用应变、能量法对无损连续油管进行疲劳寿命预测[9-10],而对有初始椭圆度及壁厚减薄的连续油管疲劳寿命的研究几乎空白。笔者依据连续油管的实际工作状态,在实验室现有的电子万能拉伸实验机CMT5105 的条件下,设计专用的疲劳实验装置,对连续油管开展弯曲—拉直疲劳寿命实验,得出连续油管椭圆度、壁厚随循环次数变化公式,从而建立了连续油管基于椭圆度及壁厚参数的低周疲劳寿命公式。
1 实验装置设计
根据连续油管在工作过程中发生拉伸—弯曲交替变形,分别设计了连续油管拉弯、校直装置。拉弯实物图如图1(a)所示,将制作好的试件放在设计好的模具上,在油管两侧设计专用的油管卡具与钢丝绳相连,钢丝绳的另一端连在拉力底座滑轮上,拉力底座通过销轴与移动横梁连接,通过计算机或控制盒调节实验机器上移动横梁向下移动,从而实现油管沿模具弧度拉弯,当油管刚好弯曲模具边缘时弯曲过程结束。
校直实物图如图1(b)所示,将被拉弯的连续油管通过导向孔,放在设计好的拉直工装上,在油管底部设计专用的油管卡具与钢丝绳相连,钢丝绳的另一端连在拉力底座滑轮上,通过计算机或控制盒调节实验机器上移动横梁向下移动,油管沿拉直工装中的路线移动,通过两排滚子对油管的相互挤压作用,从而实现连续油管由弯变直,当油管弯曲部位完全变直后,拉直过程结束。

图1 实验装置实物图
2 实验方案
将连续油管从中心位置分开,分别以50 mm 距离取3 个截面,在每个截面上标注A、B、C、D 4 点,测点分布示意图如图2 所示。利用数显千分尺对实验过程中油管长轴、短轴进行测量(见图3),根据公式(1)得到连续油管椭圆度数值。利用MT200 超声波测厚仪对连续油管A、B、C、D 4 点壁厚进行跟踪监测,求得连续油管平均壁厚数值。

式中,Φ 为连续油管椭圆度,%;d0max,d0min分别为连续油管长轴、短轴,mm;d0为连续油管直径,mm。

图2 连续油管测试分布图点

图3 椭圆横截面
3 椭圆度及壁厚随循环次数变化规律研究
基于上述实验方案对Ø60.325 mm 管开展弯曲—拉直疲劳寿命实验。图4(a)为连续管弯曲拉直对比实物图,经过数次弯曲拉直后,连续管发生断裂,其断裂如图4(b)所示。现列出其中4 个试件实验数据,其椭圆度和壁厚数据分别见图1、图2,其中,试件1~4 均为无损管,试件1、2 管内无内压,试件3、4 管内施加20 MPa 内压。

图4 连续油管实验实物图
3.1 椭圆度随循环次数变化规律研究
由图5 可看出,椭圆度随弯曲拉直次数增加而增大,试件1 在弯曲拉直次数为50 时椭圆度达到24.02%发生失效,试件2、试件3、试件4 在弯曲拉直次数分别为48、44、43 时,椭圆度分别达到23.89%、22.54%、20.44%发生失效。
基于数学回归方法对连续油管大量椭圆度数据进行拟合,得出椭圆度随弯曲拉直循环次数变化公式为

式中, k1=54;k2=82.337 2;N 为拉直—弯曲次数,次;Δεp为管弯曲—拉直塑性应变幅;Δεc=0.025 2;k3=0.02;σθ为环向应力,MPa。
依据式(2)对连续管椭圆度随弯曲拉直次数变化数值进行计算,并绘制出曲线,与实验数据进行对比,其对比曲线见图5。
由图5 可看出,利用式(2)所得到连续管椭圆度随弯曲拉直次数变化的数值与实验测得数值较符合,因此可得出,式(2)能较好地描述连续油管椭圆度随弯曲拉直次数的变化规律。

图5 试件1~4 椭圆度公式拟合及实验测得数值随弯曲 拉直次数变化对比曲线
3.2 壁厚随循环次数变化规律研究
由图6 可看出,连续油管壁厚数值随弯曲拉直次数增加而减薄,试件1、试件2、试件3、试件4 初始壁厚分别为4.55 mm、4.54 mm、4.55 mm、4.57 mm,在弯曲拉直次数分别为50、48、44、43 发生失效时壁厚分别为4.43 mm、4.42 mm、4.40 mm、4.42 mm,壁厚减薄量分别为0.12 mm、0.12 mm、0.15 mm、0.15 mm。
基于回归计算方法对连续油管壁厚数据进行拟合,得出连续油管壁厚减薄量随弯曲拉直循环次数变化公式为

式中, k1=11.22;k2=11.4;k3=30.24;k4=2.4;t0为初始壁厚,mm;σθ为环向应力,MPa;k5=0.005;p 为内压,MPa。
依据式(3)对不同弯曲拉直循环次数下连续管壁厚数值进行计算,并绘制出曲线,与对应的实验数值进行对比,其对比曲线见图6。
由图6 可看出,利用式(3)所得到壁厚随弯曲拉直次数变化的数值与实验测得数值较符合,因此可得出,式(3)能较好地描述连续油管壁厚随弯曲拉直次数的变化规律。

图6 试件1~4 壁厚公式拟合及实验测得数值随弯曲 拉直次数变化对比曲线
4 连续油管疲劳寿命影响因素分析
采用三参数幂函数能量法[8]得到连续油管低周疲劳寿命计算公式为
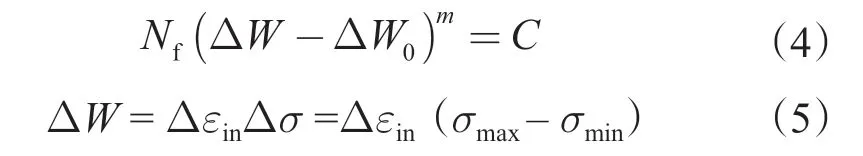
式中,Nf为连续油管的疲劳寿命;ΔW 为应变能;ΔW0为疲劳极限;m,C 为待定常数,与材料有关;Δεin为总应变幅;Δσ 为循环的最大应力幅度,MPa;σmax为最大应力,MPa;σmin为最小应力,MPa。
考虑连续油管在弯曲时产生的变形主要为塑性变形,则可忽略弹性应变,采用塑性应变幅,即

式中,Δεp为塑性应变幅。



其中

式中,NΦ、Nt分别为椭圆度、壁厚对连续油管疲劳寿命影响次数;kΦ、kt分别为椭圆度、壁厚对连续油管疲劳寿命影响的比例系数。
NΦ由图7 所示的迭代计算框图得出。

图7 椭圆度对连续油管疲劳寿命影响次数计算框图
试件5、6、7 初始椭圆度分别为8.13%、9.76%、10.16%,初始壁厚减薄量依次为0.02 mm、0.03 mm、0.04 mm,试件5、6 管内部施加内压为20 MPa,试件7 管内无压力。对试件5~7 开展疲劳寿命实验,采用式(7)~(9)及图7 的计算框图对有损伤连续油管低周疲劳寿命进行计算,与实验得到循环次数进行对比,其对比结果见表1 所示。

表1 有损伤连续油管实验及理论低周疲劳寿命对比
由表1 可得出,试件5、6、7 实验测得的弯曲—拉直次数分别为35、33、33 次,理论循环次数分别为36、33、34,其相对误差最大为3.03%。因此,可得出,所建立的计算方法能够比较准确地预测有损伤连续管低周疲劳寿命。
5 结论与认识
(1) 针对连续油管每次作业过程中经历3 次拉伸—弯曲交替变形,在实验室现有的电子万能拉伸实验机CMT5105 的条件下,设计专用的疲劳寿命实验装置,并制定实验方案,对两类连续油管试件(无损、含椭圆度)开展低周疲劳实验。
(2)基于大量的连续油管疲劳实验数据,利用数学回归方法拟合椭圆度及壁厚数值随弯曲拉直次数变化计算公式,公式(2)、(3)能较准确地计算连续油管椭圆度及壁厚随弯曲拉直次数的变化数值。
(3)根据三参数幂函数能量法建立椭圆度及壁厚参数的低周疲劳寿命公式,理论和实验结果表明:利用式(7)~(9)能够比较准确预测出有损伤连续管剩余疲劳寿命。由此,采用所建立的计算方法能够为工程连续油管失效预测及控制提供技术手段。
[1] 贺会群. 连续管技术与装备发展综述[J]. 石油机械,2006,34 (1):1-6.
[2] 王海涛,李相方.连续油管技术在井下作业中的应用现状及思考[J].石油钻采工艺,2008,30(6):120-124.
[3] 任国富,张华光,付钢旦,等. 国外连续油管作业机的最新进展[J]. 石油矿场机械, 2009, 38(2) :97-99.
[4] 杨高,罗岗. 连续管缠绕力学研究[J]. 石油矿场机械,2010,39(5):10-13.
[5] 何东升,徐克彬,魏广森,等.连续油管在水平井中作业的力学分析[J].石油钻采工艺,1999,21(3):61-65.
[6] 李小影,石凯. 连续管失效及疲劳寿命的研究现状[J].内蒙古石油化工,2008,20(6):7-11.
[7] 王海涛,李相方. 连续油管卷曲低周疲劳寿命预测[J].石油机械,2008,36 (11):25-31.
[8] PADON Tomas, LUFT Bernie, KEE Emmanuel, et al . Fatigue life of coiled tubing with external mechanical damage[R]. SPE 107113, 2007.
[9] WU J. Coiled tubing working life prediction[R]. SPE 29461, 1995.
[10] 高霞,上官丰收,宋生印. 连续管低周疲劳试验装置方案分析[J].石油矿场机械,2007,36(11):63-67.

