油品二元掺混黏度预测模型评价研究

张 俊， 曹学文， 张 楠， 李显超， 吉俊毅

（中国石油大学（华东）储运与建筑工程学院，山东青岛266580）

在石油工业中，某些工艺及处理要求油品有合适的黏度。因此，为改善油品的黏度条件，常将两种不同黏度的油品相互混合。例如，开发中提高采收率、洗井，稠油的掺稀输送、脱水，炼厂的掺混改质等［1］。

为控制并预测利用掺混油品达到工艺要求，实现工艺目的的这些过程，需要掌握油品掺混后的黏度，而问题是对于很多过程混合黏度是无法直接用仪器测量的。这也就需要对混合黏度建立相应的计算模型，来预测掺混后油品的黏度。从而指导生产实践，优化工艺及处理过程。

黏度来源于分子及其之间的相互作用，不具有简单的线性加和性［2］。因此，掺混油品的黏度预测是个难题，许多学者也在这方面做了不懈探索与研究。迄今为止，已提出诸多预测模型。

这些模型的预测精度是各不相同的，适用条件也不一样。而文献中也鲜有系统的对比评价。如何选用，孰优孰劣，让模型的使用者无所适从。本文依据室内及文献中的实验数据，按黏度比对各个预测模型进行了系统评估，得出了各个模型预测特性，并做出推荐。

1 预测模型介绍

与描述性模型不同，油品混合黏度预测模型是指那些只需知道油品各自的黏度及掺入比，而不需要通过进一步实验获得其他参数，就可以计算出混合后黏度的数学模型［3］。文献中现有的混合黏度预测模型详细介绍如下。

1.1 Arrhenius模型

Arrhenius于1887 年基于理想溶液首次提出了计算混合液体黏度的数学模型［4］。用Arrhenius模型计算混合油品的黏度时只需要知道两种掺混油品各自的黏度计掺入比例，使用较为方便。该模型的数学表达式可以表达指数函数或者对数的形式，模型公式如下所示：

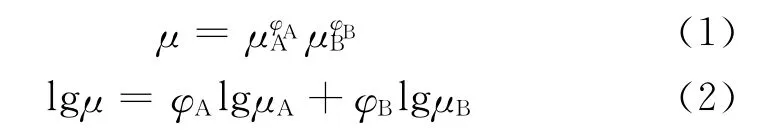
式中，φA 为油品A 的体积分数，μA 为油品A 的黏度；φB 为油品B的体积分数，μB 为油品B 的黏度，μ为混合黏度。

值得注意的是，由于Arrhenius模型自身的数学模型结构，决定了在使用模型时，其预测结果误差有两边低，中间位置处达到最大值得特征，此外Arrhenius得到该模型所运用的实验数据都是基于黏度、密度相近的有机溶剂，因此该模型对于物性相差较大的两种油品之间的掺混黏度预测的适用性有待评价。

1.2 Bingham 模型

1932 年，Bingham 摒弃了黏度可以加和的假设，将黏度的概念与电阻概念类比，结合实验数据发现黏度的倒数却是有加和性的，于是第一次从理论及实验出发提出了以倒数混合规则为基础的黏度预测模型［5］。Bingham 模型的计算也只需要知道油品各自的体积分数及黏度，使用也非常方便。该模型的数学表达式如下所示：

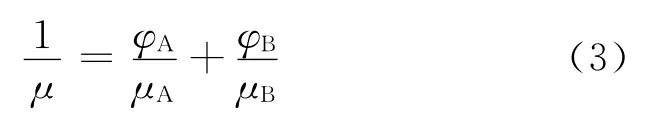
式中，φA 为油品A 的体积分数，μA 为油品A 的黏度；φB 为油品B的体积分数，μB 为油品B 的黏度，μ为混合黏度。

由模型的数学形式可以预见，在用Bingham 模型来评价两种黏度相差很大的油品掺混时，必将会产生很大的误差，其预测的效果将会随着两种油品黏度差的增大而显著恶化。可以说是一种不适用于黏度差别大的油品掺混黏度预测模型。

1.3 Kendall and Monroe模型

Kendall指出Bingham 及Arrhenius两个模型都是基于密度、黏度、相对分子质量相差不大的两种有机溶剂混合物掺混测得的黏度数据得到的，也就使得得到的模型的应用有了一定的局限性。为避开这一局限，Kendall选取了4种物性相差较大的掺混溶液进行了实验黏度的测量与分析，并用数学关系式拟合实验数据，最终发现对黏度进行指数运算的混合关系式最符合实验数据，于是提出以下模型［6］。该模型的计算只需要知道油品各自的体积分数及黏度，使用方便。模型的数学表达式如下所示：

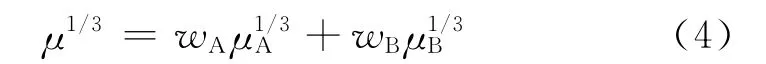
式中，wA为油品A 的质量分数，μA 为油品A 的黏度；wB为油品B的质量分数，μB 为油品B的黏度，μ为混合黏度。

在该模型中Kendall认为μ1／3是具有加和性的，Kendall突破了基于理想溶液的限制提出了一种新的模型，但是应当注意上述的3个模型的得出都是基于的有机溶剂的实验数据，对于油品掺混黏度的预测的适应性也有待评估。

1.4 Cragoe模型

Cragoe创造性的定义了一种表征流体流动能力的流函数L，将黏度关系与流函数相关联，认为这种流函数是具有加和性的，从而提出了一个新的混合黏度预测模型［7］。该模型的计算只需要知道油品各自的体积分数及黏度，使用方便。模型的数学表达式如下所示：

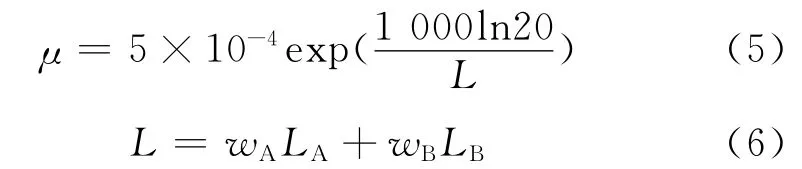
式中，L 为塔混后油品的流函数；LA为油品A 的流函数；LB为油品B 的流函数；wA为油品A 的质量分数，μA 为油品A 的黏度；wB为油品B 的质量分数，μB 为油品B的黏度，μ 为混合黏度。

Cragoe模型的提出是基于一系列油品掺混实验数据得到的，较上述3个模型有较大的进步和突破。但是该模型对任意两种油品掺混黏度预测的精度仍然需要考察，并与其他模型进行对比研究。

1.5 Shu模型

W.R.Shu［8］在Lederer方程的基础上，通过结合Einstein方程，将油品黏度混合过程类比为悬浮小颗粒在溶剂中被无限稀释，并运用实验数据回归计算出了将Lederer方程中的未知经验参数α的一般关系式，提出了另一种混合黏度预测模型。该模型的计算只需要知道油品各自的密度及黏度，使用方便。该模型的数学表达式如下所示：

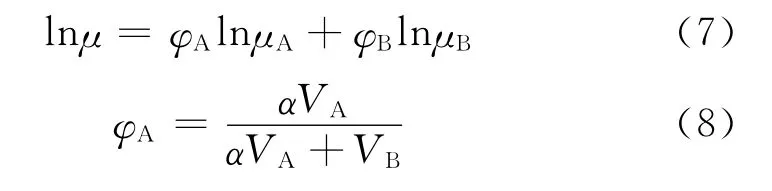
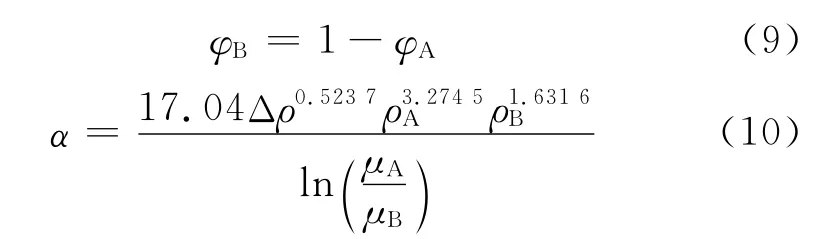
式中，α为经验参数；ρA 为油品A 的密度，μA 为油品A 的黏度，VA为 油 品A 的 体 积 分 数，φA 为 油 品A的体积分数；ρB 为油品B 的密度，μB 为油品B 的黏度，VB为油品B的体积分数，φB 为油品B的体积分数，μB 为油品B的黏度；Δρ＝ρA－ρB 为油品A 与油品B的密度差。

Shu模型是基于黏度差各异的二元油品掺混的实验数据，在实验数据基础中甚至包括了油砂沥青油与稀油掺混的实验数据。Shu认为该模型的准确性较好，可以适用于黏度相差特别大，如稠油掺稀的情况。

1.6 Chirinos模型

Chirinos通过一些实验测量值发现，对黏度进行双对数关系运算可以很好的进行混合黏度的预测［9］。该模型的计算只需要知道油品各自的体积分数及黏度，使用方便。该模型的数学表达式如下所示：

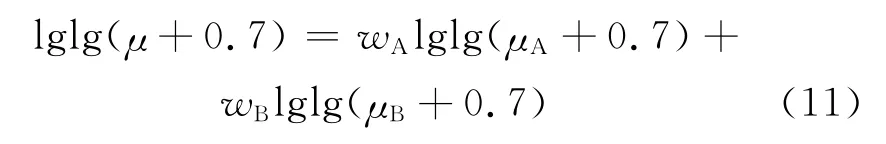
其中，wA为油品A 的质量分数，μA 为油品A 的黏度；wB为油品B的质量分数，μB 为油品B的黏度，μ为混合黏度。

Chirinos模型可以对黏度相差较大的两种油品的掺混黏度进行预测，但是它只能在有限的黏度差范围内使用，否则将不能取得较好的预测效果。

1.7 Latour模型

Latour在Cragoe的研究基础上，通过实验数据回归得出了黏度交互影响参数的一般计算关系式，他通过99组实验数据点的分析发现对黏度取双对数运算后与掺入组分分数有近似线性的关系，为了增强这一线性关系，引入了黏度降低系数n，从而使得组分分数的n次幂与黏度取双对数后的值更具有线性关系，据此提出自己的模型［10］。该模型的计算只需要知道油品各自的密度及黏度，使用方便。该模型的数学表达式如下所示：

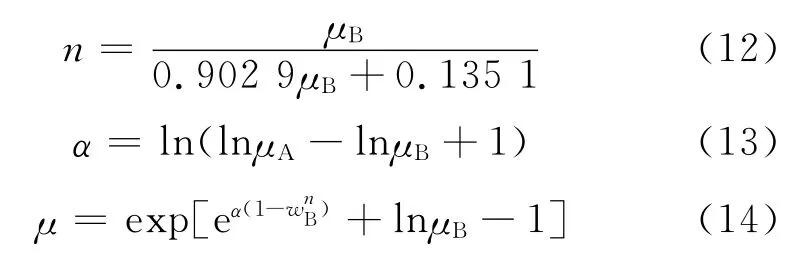
其中，μA 为油品A 的黏度；wB为油品B 的质量分数，μB 为 油 品B 的 黏 度，α 为 黏 度 交 互 影 响 参 数，n为黏度降低系数，μ 为混合黏度。

该模型可以用于沥青与稀油之间的掺混黏度预测，可以获得一定的预测精度。但是，其预测效果的稳定性及精度的可接受性仍然有待评估验证，是一个需要深入研究的问题。

1.8 Chevron模型

Chevron模型引入了黏度掺混系数，不直接对黏度进行混合计算，最后通过一个数学关系式油混合的黏度掺混系数计算出掺混黏度［11］。该模型的计算需要知道油品各自的体积分数及黏度，使用方便。模型的数学表达式如下所示：

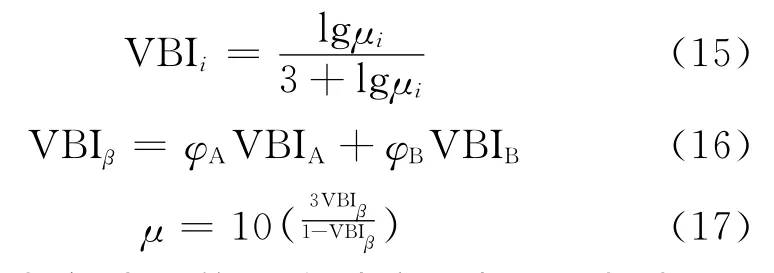
其中，VBIi为各油品的混合黏度系数，μi 为油品i的黏度，VBIA为油品A 的混合黏度系数，VBIB为油品B的混合黏度系数，φA 为油品A 的体积分数，μA为油品A 的黏度；φB 为油品B 的体 积分数，μB为油品B的黏度，VBIβ为混合黏度系数，μ 为混合黏度。

Chevron模型应用于炼厂的情况比较多，因此，对于炼厂中油品的掺混黏度计算可以取得较好的精度。

2 模型评价

模型的评价需建立一套完整的评价方法与准则，并且需要大量的不同掺混情况下的实验数据为基础。另外，在评价数据的选取方面也应科学选择。下面以黏度比及相对误差的绝对值建立评价方法与准则，选取同一温度下的不同油品掺混的实验数据进行模型的评价。

2.1 评价方法与标准

本文按照黏度比区分模型应用的不同情形，以相对误差为评价准则，对上述预测模型进行逐一评价。

黏度比，是指较高黏度油品黏度与较低黏度油品黏度的比值［12］。这里定义下标A 表示较黏油品的黏度，下标B 表示较稀油品的黏度。因此，黏度比的计算表达式如下所示：

预测相对误差，是指实验测量值与预测计算值之差与实验测量值的比。计算表达式如下：

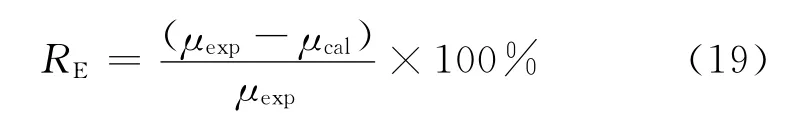
为方便并兼顾工程实际情况，本文将黏度比分为＜10、10～102、102～103、103～104、104～105、105～106等6个量级。分析每个预测模型在这6个量级下的预测特性及其随黏度比变化的情况，从而获得每个预测模型的自身精度及适用工况，做出使用推荐。

2.2 评价数据的选取

黏度是温度的函数，温度增大黏度减小，模型的预测效果也随之变化，文献［13］研究表明，当温度升高时，各模型的预测效果将有所改善。所以评价时应选取同一温度下的不同黏度比的掺混油品的实验数据进行评价才具有可比性。

因此，从文献［13－14］中获得25 ℃下的全黏度比范围内的实验数据对各个预测模型进行评价。

评价数据所用的油品基本物性参数如表1 所示。

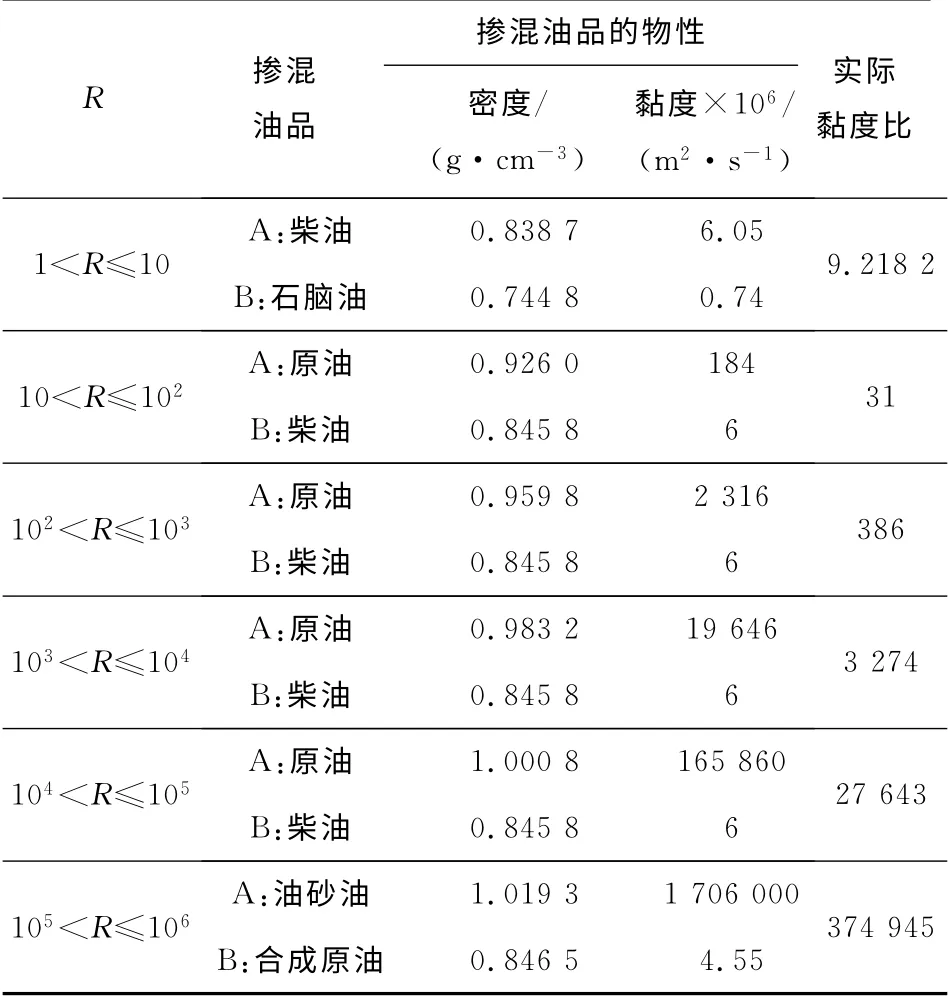
表1 不同黏度比所用掺混油样的物性参数Table 1 Blending oil sample for different viscosity ratio

相对应的掺混实验数据如表2所示。

2.3 评价结果

通过编制各模型的Matlab计算程序，输入数据库中的实验数据，可以计算出各个模型的预测黏度计相对误差，从而得到各模型的预测特性及精度。以黏度比为划分，不同模型的预测特性及精度分析如下。

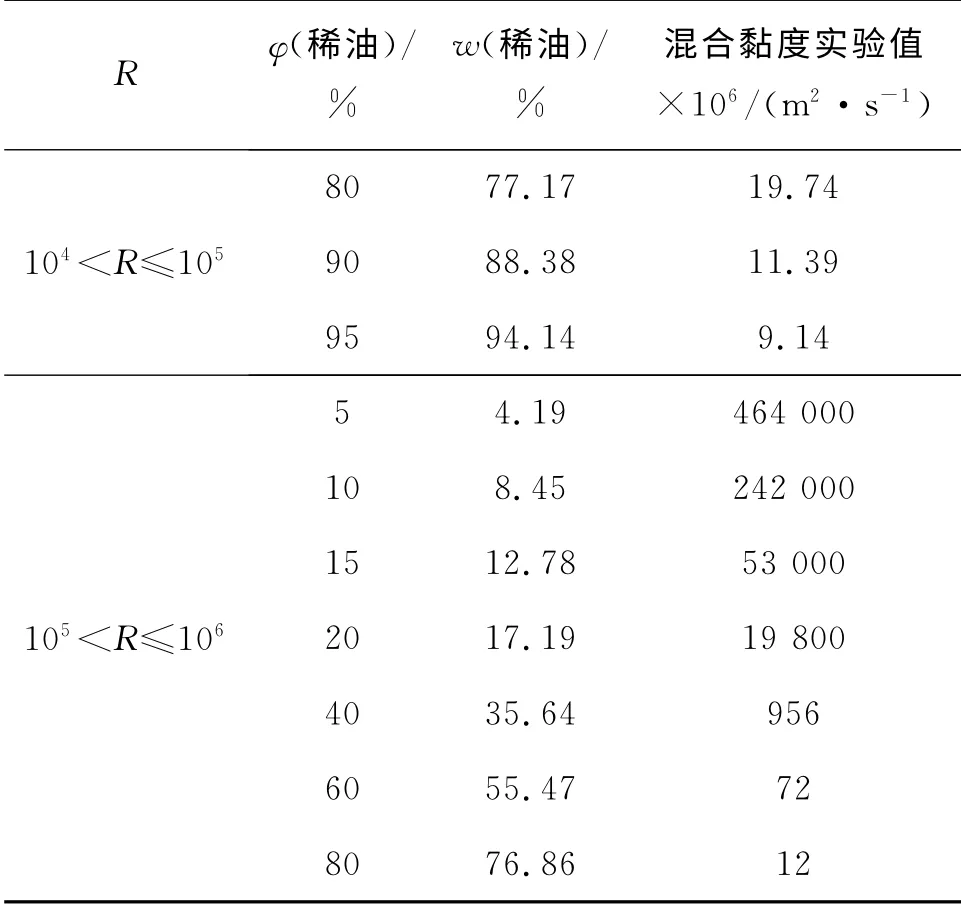
黏度比1＜R≤10时，以掺入比为横坐标，相对误差的绝对值为纵坐标，工程误差20%为基准线，做出各模型预测特性及精度对比结果如图1所示。

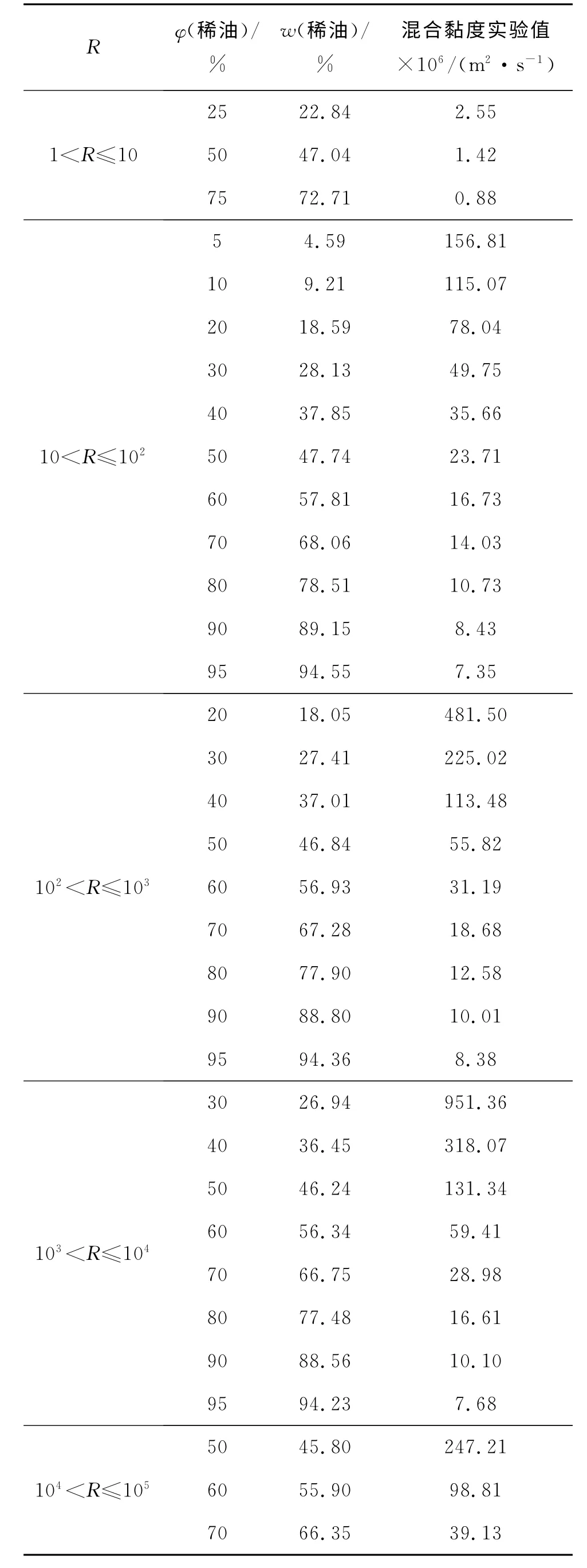
表2 模型评价掺混黏度实验数据Table 2 Blending data for evaluating different models

续表2

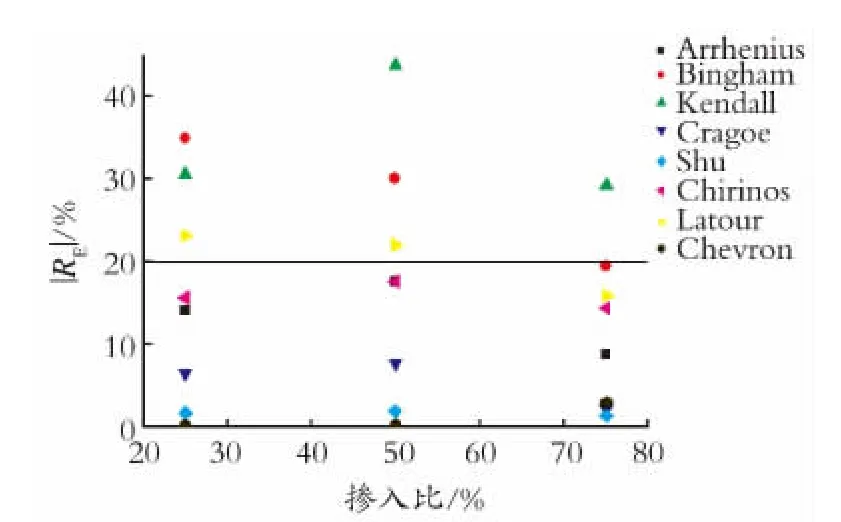
图1 黏度比1＜R≤10各模型相对误差的绝对值对比Fig.1 Comparison of absolute average deviation of different models at 1＜R≤10

由图1可以看出，在1＜R≤10下，Arrhenius、Chirinos、Cragoe、Shu、Chevron模型的误差能控制在20%内，其中Shu、Chevron的效果较好能在5%之下，且Chevron相对误差的平均值较小，Latour、Bingham、Kendall模型预测较差，超过了可接受范围。

这些模型中，Kendall、Arrhenius的预测波动较大，在掺入比50%处出现最大误差，Bingham 的预测误差虽掺入比增大而降低，但整体误差均很大。其他模型在不同黏度比下预测误差整体平稳。

黏度比10＜R≤102时，模型预测特性及精度对比结果如图2所示。

由 图2 可 见，黏 度 比1 0 ＜R ≤1 02时，Arrhenius、Bingham、Kendall模型的预测误差超限，其中Kendall模型的相对误差绝对值都有超过100%，其他5个模型预测误差大体能控制在20%，其中Chevron模型的平均相对误差能控制在5%以下。

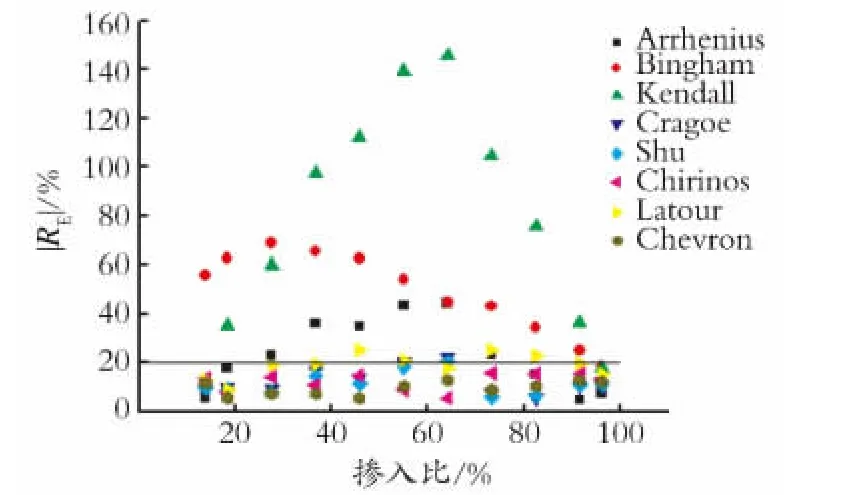
图2 黏度比10＜R≤102 各模型相对误差的绝对值对比Fig.2 Comparison of absolute average deviation of different models at 10＜R≤102

进一步计算研究发现由于Kendall模型的自身局限性，其随着黏度比的不断增大，相对误差将进一步扩大。因此，在后面的评价中将剔除Kendall模型。

黏度比102＜R≤103时，对比结果如图3所示。

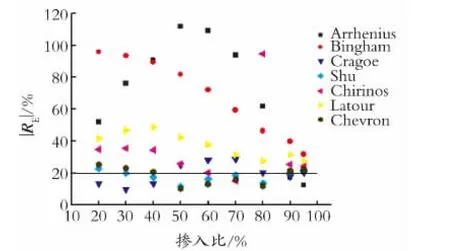
图3 黏度比102＜R≤103 各模型相对误差的绝对值对比Fig.3 Comparison of absolute average deviation of different models at 102＜R≤103

由图3可见，只有Chevron、Shu模型的预测误差较好的控制在了20%以内，其他模型预测误差的绝对值均有超过20%。

黏度比103＜R≤104时，对比结果如图4所示。

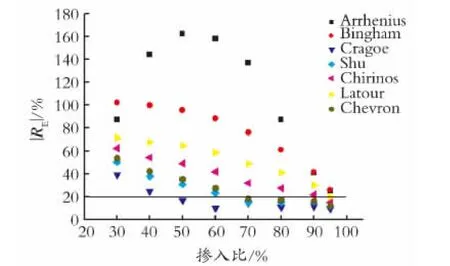
图4 黏度比103＜R≤104 各模型相对误差的绝对值对比Fig.4 Comparison of absolute average deviation of different models at 103＜R≤104

由图4可以看出，所有模型中，只有Cragoe模型的相对误差绝对值在20%上的点最少，其平均相对误差绝对值也最小。随着黏度比的增大，Arrhenius模型预测误差超过100%的点增多，在后续评价中将剔除。

黏度比104＜R≤105时，对比结果如图5所示。

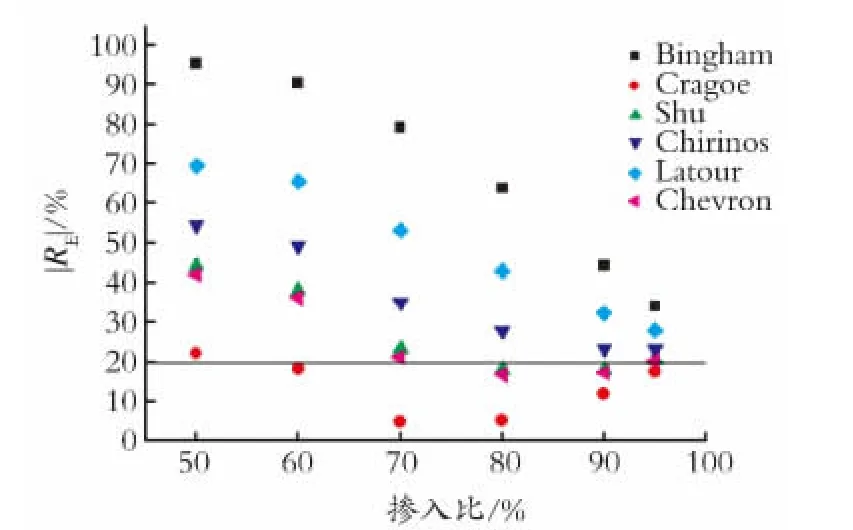
图5 黏度比104＜R≤105 各模型相对误差的绝对值对比Fig.5 Comparison of absolute average deviation of different models at 104＜R≤105

由图5可以看出，在黏度比104＜R≤105下，只有Cragoe模型的误差绝对值能够控制在误差可接受范围内。Bingham模型的偏差太大，相对误差也接近100%，在后续的评价中剔除。

黏度比105＜R≤106时，对比结果如图6所示。

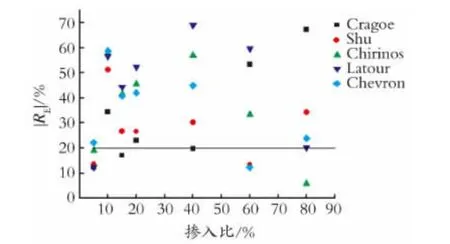
图6 黏度比105＜R≤106 各模型相对误差的绝对值对比Fig.6 Comparison of absolute average deviation of different models at 105＜R≤106

由图6可知，在超高黏度比105＜R≤106的情况下，各模型的预测稳定性都变差，不同掺入比的预测误差波动较大，且几乎没有一个模型能保证所有掺入比下预测误差在20%范围内。这一黏度比下的预测模型有待完善与开发。

［1］ Motahhari H，Schoeggl F F，Satyro M A，et al.Prediction of the viscosity of solvent diluted live bitumen at temperatures up to 175 ℃［J］.SPE 149405，2011.

［2］ Methrotra A K.Development of mixing rules for predicting the viscosity of bitumen and its fractions blended with toluene［J］.Can.J.Chem.Eng.，1990，68（5）：839－848.

［3］ Rahmes M H，Nelson W L.Viscosity blending relationships of heavy petroleum oils［J］.Analytical Chem.，1948，20（10）：912－915.

［4］ Sunny Goh Eng Giap.The hidden property of arrhenius－typr relationship：viscosity as a function of temperature［J］.Journal of Physical Science，2010，21（1）：29－39.

［5］ Bingham E C.The viscosity of binary mixtures［J］.J.Phys.Chem.，1914，18（2）：157－165.

［6］ Kendall J，Monroe K.The viscosity of liquids II.The viscosity－composition curve for ideal liquid mixtures［J］.Am.Chem.J.，1917，39（9）：1787－1802.

［7］ Cragoe C S.Changes in the viscosity of liquids with temperature，pressure and composition［C］.1st World Petroleum Congress，London，UK：［s.n.］.1933：18－24.

［8］ Shu W R.A viscosity correlation for mixtures of heavy oil，bitumen，and petroleum fractions［J］.SPE 11280，1984.

［9］ Sutton R P，Bergman D F.Application of the Bergman－Sutton method for determining blend viscosity［J］.SPE 117711，2008.

［10］ Miadonye A，Latour N，Puttagunta V R.A correlation for viscosity and solvent mass fraction of bitumen－diluent mixtures［J］.Pet.Sci.Technol.，2000，18（1－2）：1－14.

［11］ Hossain M S，Sarica C，Zhang H Q.Assessment and development of heavy oil viscosity correlations［J］.SPE 97907，2005.

［12］ Wen Y，Kantzas A.Evaluation of heavy oil／bitumen－solvent mixture viscosity models［C］.55th Annual Technical Meeting，Calgary，Alberta，Canada：［s.n.］，2004：8－10.

［13］ Centeno G，Gabriela Sánchez－Reyna，Ancheyta J，et al.Testing various mixing rules for calculatiuon of viscosity of petroleum blends［J］.Fuel，2011，90（12）：3561－3570.

［14］ Barrufet M，Setiadarma A.Reliable heavy oil－solvent viscosity mixing rules for viscosities up to 450 K，oil－solvent viscosity ratios up to 4×105，and any solvent proportion［J］.Fluid Phase Equilibria，2003，213（1－2）：65－79.