基于遗传小波神经网络的电网故障诊断方法研究
刘晓琴, 王大志, 张翠玲, 江雪晨, 宁 一
(1.东北大学信息科学与工程学院,辽宁沈阳110819;2.辽宁石油化工大学信息与控制工程学院,辽宁抚顺113001)
电网规模日益扩大,其复杂性不断提高,获取的实时数据规模也越来越大,远远超出了技术人员的处理能力,且故障时继电保护和断路器的拒动、误动以及信息上传过程中的丢失、畸变等增加了技术人员分析判断故障的难度。研究和开发故障诊断系统给技术人员判断故障和动态监控系统提供必要条件[1]。电网发生故障时,快速、准确地诊断系统故障对于电网安全运行具有重要意义。
故障诊断方法如专家系统、人工神经网络、基于优化的方法以及由于信息的不确定性和不完备而采取的基于模糊集、信息理论、粗糙集的方法等已用于研究电力系统故障诊断。文献[2]引入信息理论来研究电力系统故障过程中的不确定性,提出了基于信息损失最小的电网故障诊断原理,研究了电网故障诊断过程中信息损失的规律。单一的智能方法在电力系统故障诊断存在局限性,多种智能方法优化已经用于电力系统的故障诊断[3]。文献[4]提出小波对电流量进行分解,将分解到小波系数输入到PNN 神经网络。文献[5]推导并建立了RBF 神经网络和模糊控制系统之间的等值关系,使得蕴含在RBF神经网络权重中的知识转变为等值模糊控制系统中用语言表述的规则,提出RBF神经网络的局部重新训练新算法。文献[6]用模糊算法实现RBF神经网络的局部优化。文献[1]对上述几种方法的优缺点进行了评价。
以训练小波BP网络为例来说明用遗传算法优化小波神经网络的思想与方法。用母小波取代传统的Sigmoid函数,所建的小波神经网络具有更强的非线性逼近能力。用遗传算法优化小波神经网络,可以使得神经网络具有自进化、自适应能力,从而构造出进化的小波神经网络,它主要包括3个方面的进化:连接权的进化,网络结构的进化和尺度函数、位置函数的进化。提出用遗传算法优化小波神经网络的目的是能够提高收敛速度和诊断准确率。
1 故障诊断系统的总体构成
1.1 算法原理

从小波神经网络的模型可得到:

式(1)中,隐层第m 个节点的阈值为θm;输出层第j个节点的阈值为θj。P 是输入样本总数,式(1)计算可得输出层第j 个节点,第p(p=1,2,…,P)个样本的输出,即opj,^opj是其目标输出值,误差能量函数定义表达式为:

I,M,J 分别是神经网络的输入、隐层和输出层神经元个数。在小波神经网络中,电力网络中所有继电器和断路器的总数等于I,这些继电器和断路器的状态(0或1)作为神经网络的输入信号;电力网络中系统元件等于J,这些元件的状态(故障或完好)是诊断的目标。
1.2 小波神经网络结构优化
在采用小波神经网络构建故障诊断系统中,层间的权值、尺度参数、位置参数使用遗传算法优化[7-8]。依次排好尺度参数、位置参数和权值顺序,按一定编码规则生成染色体,把染色体解码后的各权值、尺度参数、位置参数代入诊断系统后,把实际输出与期望输出的差值相关的函数定义为适应度函数,当条件满足时停止遗传。适应度最高的染色体所对应的各权值、尺度参数、位置参数是故障诊断系统算法的全局最优解[9-10]。
2 计算机仿真结果
2.1 算例
图1 所示线路系统引用文献[11],有28 个元件、40个断路器和84个保护。

图1 系统线路图Fig.1 System circuit diagram
用S1—S28表示元件编号:Al,…,A4;Bl,…,B8;Tl,…,T8;Ll,…,L8。C1—C40表示断路器编号:QFl,QF2,…,QF40。84个保护中,36个为主保护,48 个为后备保护。36 个主保护依次编号为(r1—r36):Alm,…,A4m;Blm,…,B8m;T1m,…,T8m;L1Sm,L1Rm,…,L8Sm,L8Rm。r37—r84表示48 个后备保护:L1Sp,L1Rp,…,L8Sp,L8Rp;T1p,…,T8p;L1Ss,L1Rs,…,L8Ss,L8Rs;Tls,…,T8s。
母线用A 和B 表示,变压器用T 表示,线路用L 表示。S 表示线路发送端,R 表示线路接受端。主保护用下标m 表示,第一后备保护用p表示,第二后备保护用s表示。研究故障元件在故障区域的情况,即故障区域己经明确。
2.2 仿真结果分析
以A3故障为例说明仿真过程
(1)识别故障区域
当系统发出警报信号:保护T5s、T6s动作,断路器CB22、CB23、CB24,CB25跳闸形成故障区域。
根据跳闸断路器形成的故障区域中,需要进行故障诊断的元件为A3、B5,B6依次编号为(s1—s3),10个断路器(CB21—CB30)依次编号为(c1—c10),5个保护(A3m、B5m、B6m、T5S、T6S)依次编号为(r1—r5)。
(2)4个元件的保护动作原理
动作原理分别如表1、表2所示。

表1 主保护原理Table 1 The main protection principle
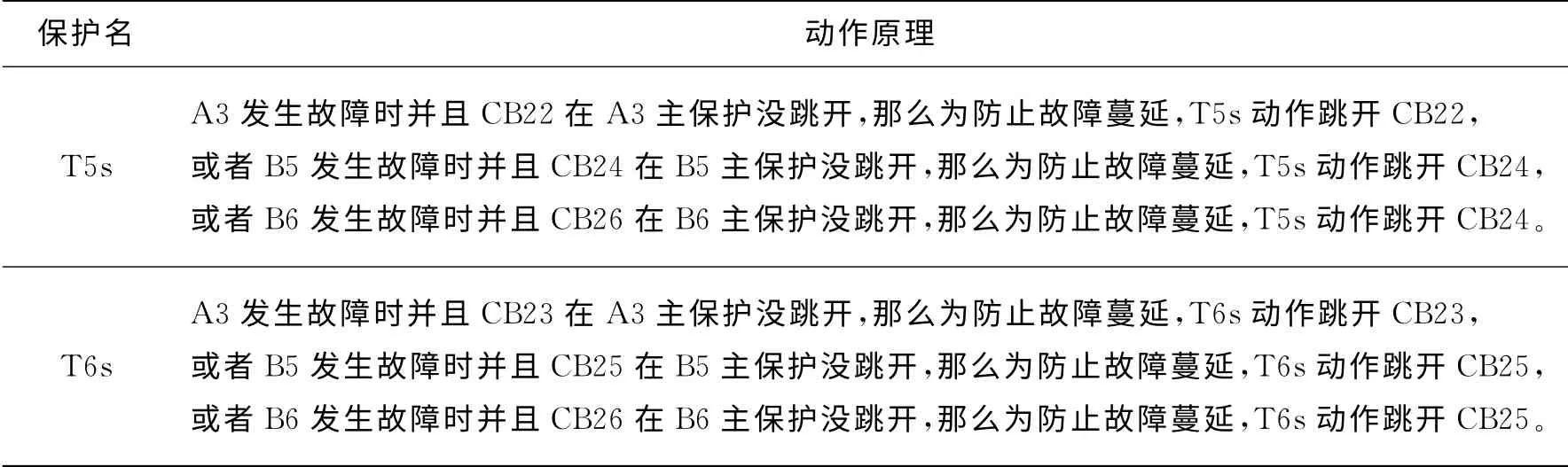
表2 第二后备保护原理Table 2 The second backup protection principle
(3)确定各个保护和断路器实际状态向量
(4)保护和断路器期望状态向量的确定
保护和断路器的实际状态向量是根据警报条件是从故障诊断图形数据库中读出的。实际状态向量如式(3)所示:

优化目标函数是根据保护动作原理及关联分析形成的,主保护期望状态如式(5)所示:

保护实际状态向量如式(4)所示:
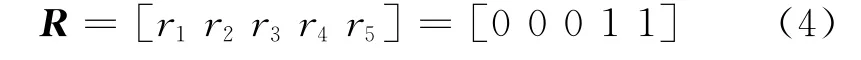
第二后备保护的期望状态如式(6)所示:
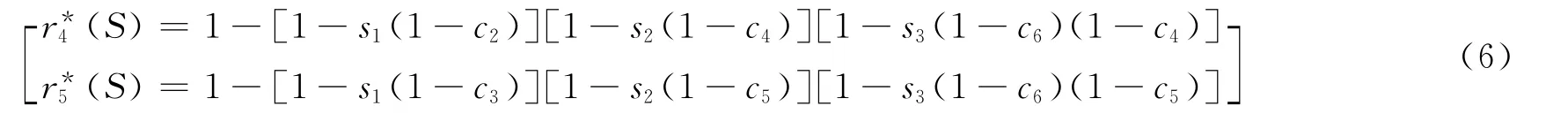
由保护触发的断路器的期望状态如式(7)所示:

(5)算法参数的设置
用计算机进行仿真,在35种典型故障案例中,3种复杂故障作为训练样本(N=3)。故障诊断系统的输入(X=124)选用保护和断路器的状态(0 或1),输出(O=28)对应28个元件的状态。
种群规模:m_nPopSize=40;
染色体长度:m_nChromLength=4;
最大进化代数:m_nMaxGeneration=10;
交叉概率:m_PCross=0.9;
变异概率:m_PMutation=0.01。
用轮盘赌方法选择算子随机产生一个[0,1]之间的值,作为轮盘赌的选择指针,选择概率是个体适应度除以累计适应度的商,交叉算子采用单点交叉方式。
对于给定的训练样本,循环收敛于最优结构,即小波神经网络具有13个隐含层。为检验故障诊断系统的泛化能力,测试样本选取了不存在于训练样本集的3个测试样本,如表3所示。

表3 故障样本Table 3 The fault samples

表4 混合故障诊断系统对于测试样本的诊断输出Table 4 The test sample output of hybrid fault diagnosis system
2.3 与神经网络诊断结果比较
采用BP 算法的神经网络构建故障诊断系统,与小波网络进行比较,结果如表4、5所示。小波网络和BP网络都设定最大容许误差为10-6,学习率是0.05,动量因子是0.98。令BPNN 也具有最优的神经网络结构,对应的误差收敛曲线如图2所示。图2(a)所示是误差达不到10-6,图2(b)所示曲线虽然收敛但误差达到0.000 3,与优化算法的最大误差相比较大。

表5 BPNN 神经网络对测试样本的输出Table 5 The test sample output of BPNN network
3 结论
小波和神经网络相结合构成故障诊断系统,遗传算法优化该小波神经网络的结构、连接权值、参数。在算例测试系统的计算机仿真结果表明,混合故障诊断系统优于BP 神经网络方法,能够较好地解决故障诊断问题。

图2 BPNN 收敛曲线Fig.2 BPNN convergence curve
[1] McArthur S D,Davidson E M,Hossack J A,et a1.Automating power system fault diagnosis through multi-agent system[C].Proceedings of the 37th Annual Hawaii lnternational Conference on System Sciences,USA:[s.n.],2004.
[2] Gao Zhanjun,Chen Qing,Cheng Tingting,et al.A uniform information model for power grid fault diagnosis[J].Automation of Electric Power Systems,2010,34,49-52.
[3] Cardosog J.Application of neural-network modules to electric power system fault section estimation[J].IEEE Trans on Power Delivery,2004,19(3):1034-l041.
[4] 杨光亮,乐全明,郁惟镛,等.基于小波神经网络和故障录波数据的电网故障类型识别[J].中国电机工程学报,2006,26(10):99-103.
[5] 毕天姝,倪以信,吴复立,等.基于径向基函数神经网络和模糊控制系统的电网故障诊断新方法[J].中国电机工程学报,2005,25(14):12-18.
[6] Mahanty R N.Dutta Gupta P B.Application of RBF neural network to fault classification and location in transmission lines[J].IEE Proceedings on Generation,Transmission and Distribution,2004,151(2):201-212.
[7] Maria Paula da Costa Couto.Review of input determination techniques for neural network models based on mutual information and genetic algorithms[J].Neural Comput &Applic,2009,16(18):891-901.
[8] Nameer Eman N E,Rasheed A S.Computing an adaptive mesh in fluid problems neural network and genetic algorithm with adaptive relaxation[J].International Journal on Artificial Intelligence Tools,2008,17(6):1089-1108.
[9] 张玉祥.小波神经网络遗传算法及其在矿山压力预报中的应用[J].中国有色金属学报,1999,9(2):448-452.
[10] 周立群,张晓琴,李书臣,等.基于粒子群优化的神经网络容错控制算法[J].石油化工高等学校学报,2011,24(3):95-98.
[11] 文福拴,韩祯祥.基于遗传算法和模拟退火算法的电力系统故障诊断[J].中国电机工程学报,1994,14(3):29-35.

