矩阵方程AXB+CXT D=E 自反最佳逼近解的迭代算法

杨家稳

（滁州职业技术学院 基础部，安徽 滁州 239000）

0 引言

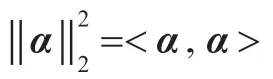
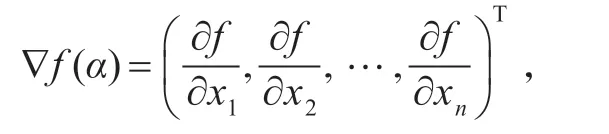
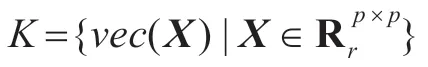
本文考虑如下问题：

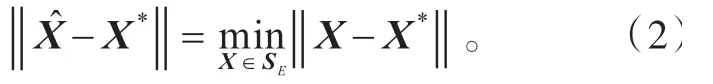
关于反射矩阵的自反矩阵或反自反矩阵在系统与控制理论、工程、科学计算等领域都有广泛的应用［1－2］。近年来，Sylvester 矩阵方程是计算数学研究的热点之一，并且取得很多成果。若矩阵方程是相容的，文献［3］利用广义Moore－Penrose给出了AX+XTC=B 解的表达式，文献［4－5］用共轭梯度迭代算法给出矩阵方程AXB+CXTD=E 极小范数最小二乘解，文献［6］给出了XA+AXT=0 的一般解，文献［7］给出AXB+CXTD=E 的可解性，文献［8］给出求解方程A1X1B1=C 、A2X2B2=D 的自反（或反自反）的最佳逼近解。若矩阵方程是不相容的，对于任意给定矩阵，文献［9］提出一种算法求ATXB+BTXTA=D 的最佳逼近解，文献［10］提出一种算法求AXB+CXD=E 自反（或反自反）的最佳逼近解。

1 迭代算法

本节首先给出解决问题Ⅰ和Ⅱ的迭代算法，然后证明该算法收敛，最后研究如何计算到非空凸集K 上的投影。具体算法步骤如下：

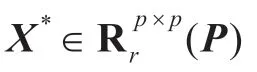
步骤2 计算

步骤3

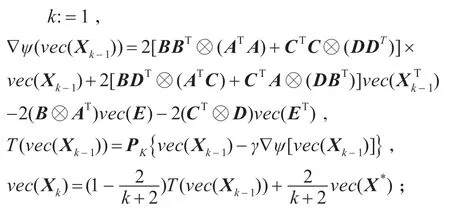
步骤4 若‖Xk-Xk-1‖＜ε ，则停止；否则，k:=k+1，转向步骤3。

为了证明算法的收敛性，首先给出下面的定义和定理。

定义1 若∀x1，x2∈S ⊂H ，∃κ ＞0 ，使得‖T(x)-T(y) ‖≤κ‖x-y ‖成立，则映射T:H →H称为κ-Lipschitzian（或κ-Lipschitzian 连续）。特别地，若对于一切x，y ∈H ，有‖T(x)-T(y) ‖≤‖x-y ‖成立，则映射T:H →H 称为非扩展映射。

定义2 对于给定的集合S ⊂H ，若∀x，y ∈S，∃η ＞0 ，使F(x)-F(y)，x-y ≥η‖x-y‖2成立，则称映射F:H →H 在集合S 上η 强单调。

定理1［11］（HSDM）设T:H →H 是非扩展映射，且Fix(T)≠∅。又设函数θ:H →R ∪∞存在Gâteaux 导数θ′:H →H ，且θ′ 在T(H) 上满足κ-Lipschitzian ，且η 强单调。对于任意的u0∈H和正实数序列(λn)n≥1满足：

或者

则由

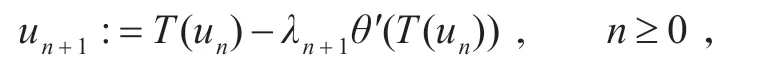
生成的序列(un)n≥0强收敛于唯一的u*，其中u*满足θ(u*)=inf{θ(Fix(T))} 。

定理2［12］设K ⊂H 是闭凸子集，又设：

（i）ψ:H →R ∪{ }∞ 是Gâteaux 可微的凸函数且 它 的 导 数 ψ′：H →H 在 H 上 满 足γ-Lipschitzian，

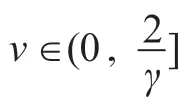
引理1 设ψ(νec(X))=‖AXB+CXTD-E‖2，则有

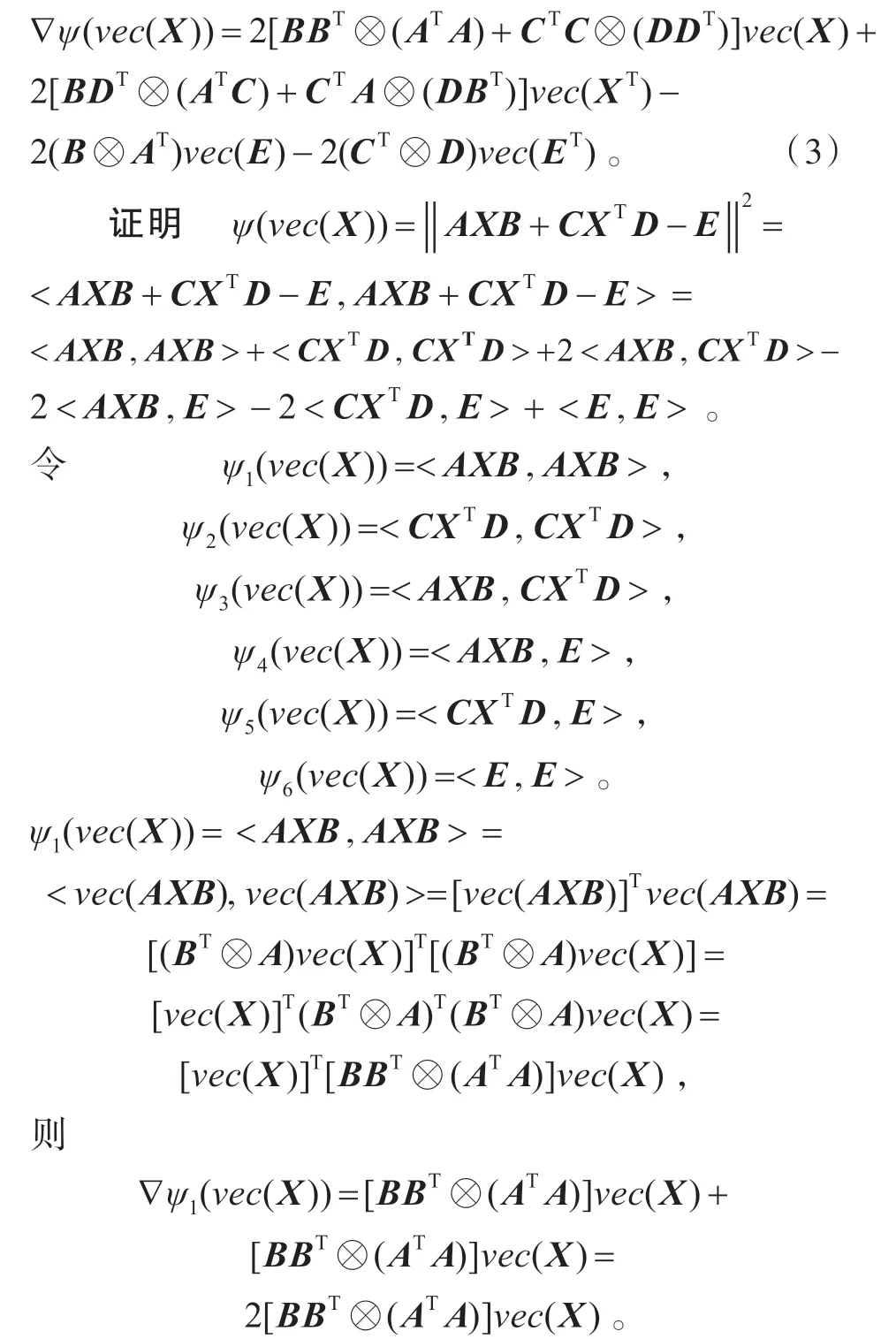
同理，可得

▽ψ2(νec(XT))=2[DDT⊗(CTC)]νec(XT)，

所以▽ψ2(νec(X))=2[CTC ⊗(DDT)]νec(X)。

依次计算可得

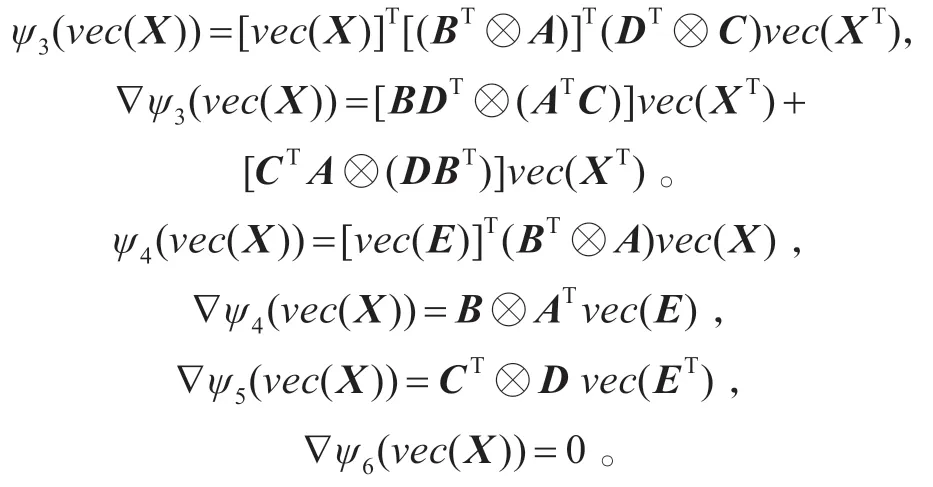
则（3）式得证。

引理2 设θ(νec(X))=‖‖X-X*2，则

证明 θ(νec(X))=‖‖X-X*2=＜X-X＊，X-X＊＞= ＜νec(X-X＊)，νec(X-X*)＞=[νec(X-X*)]T[νec(X-X*)]。

则（4）式得证。

可以证得：

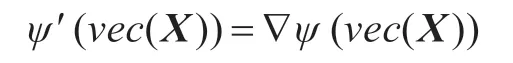
和

因此，分别用▽ψ(νec(X)) 和▽θ(νec(X)) 来代替ψ′(νec(X))和θ′(νec(X))。

引理3 设ψ(νec(X))=‖AXB+CXTD-E‖2，θ(νec(X))=‖‖X-X*2，则有如下结论：

（a）ψ(νec(X))是凸函数；

（b）θ(νec(X))是凸函数；

（c）▽ψ(νec(X))是γ-Lipschitizian；

（d）▽θ(νec(X))是κ-Lipschitzian；

（e）▽θ(νec(X))是η 强单调的。

证明 由凸函数的定义，可以证明（a）、（b）成立。

（c）令

根据（3）式有

因此，▽ψ(νec(X)) 是γ-Lipschitizian ，其中γ=‖ ‖M1+‖ ‖M2。

（d）由（4）式有

因此，▽θ(νec(X)) 是κ-Lipschitzian ，其中κ=2。

（e）由（4）式可以得到

根据定义2，可以推出▽θ(νec(X)) 是η 强单调的，其中η=2。

证明由引理1 ～3 可知，ψ(νec(X)) 和θ(νec(X))满足定理2 的条件，由定理2 可以推出算法是收敛的。

在算法中需要计算到凸集K 上的投影。为此给出如下定理：

其中，α1，α2，…，αs是矩阵(I-PT⊗P) 零空间的标准正交基。

证明 由自反矩阵的定义有

（7）式改写成

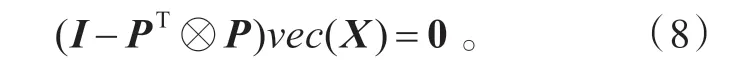
凸集K 中的元素就是线性方程（8）的解。因此只要给定（8）式解集合的标准正交基，就可以利用（5）式计算出νec(X0)在K 上的投影。

2 数值举例

下面用两个数值例子来验证上述算法的可行性，所有实验都在MATLAB2007R 中进行。

例1 考虑矩阵方程AXB+CXTD=E，其中

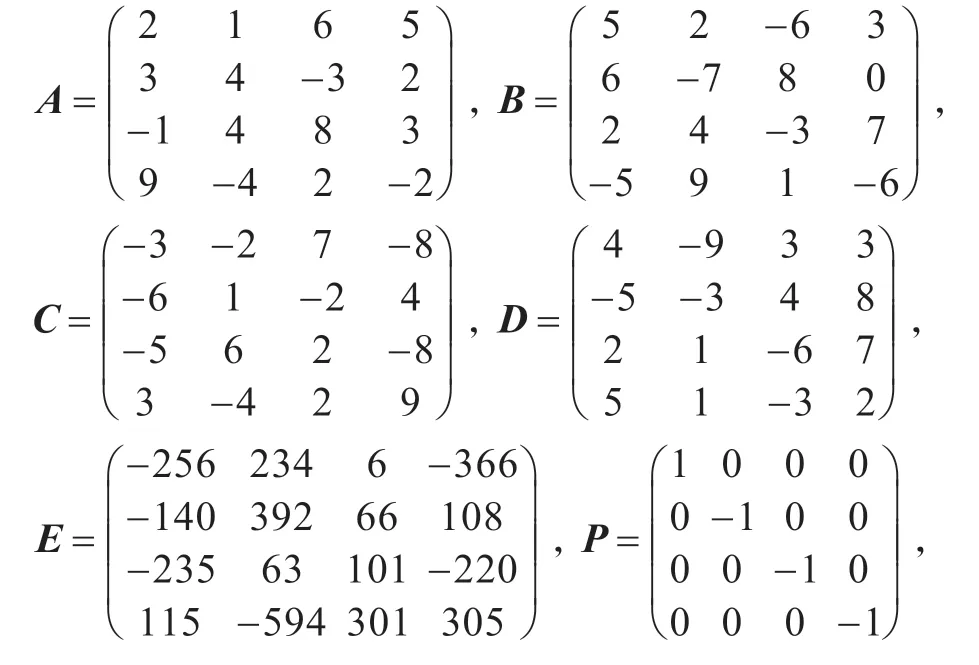
是矩阵方程相容的解。

利用算法，令ε=1.0e-11，可得

相应的余项为

例2 仍然考虑矩阵方程AXB+CXTD=E ，其中A，B，C ，D，P 和X0同例1，

可以证明上述矩阵方程是不相容的。令ε=1.0e-10，由算法得

相应的余项

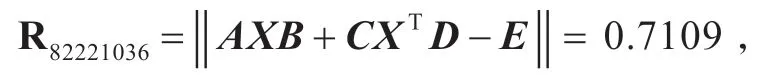
3 结语

本文利用HSDM，给出求解矩阵方程AXB+CXTD=E 自反（或反自反）最佳逼近解的迭代算法。无论方程AXB+CXTD=E 是否相容，所给的算法都可以计算其自反（或反自反）的最佳逼近解。实例说明了算法的可行性，但该算法的缺点是收敛速度较慢。文中自反（或反自反）矩阵的集合是凸集。若其他矩阵方程的未知约束矩阵是凸集，则可以应用HSDM 解决其最佳逼近问题。

［1］ Chen H C.Generalized reflexive matrices：special properties and applications［J］. SIAM J Matrix Anal Appl，1998，19（1）：140－153.

［2］ Chen H C. The SAS domain decomposition method for structural analysis［R］. Urbana：University of Illinois，1988.

［3］ Piao F X，Zhang Q L，Wang Z F. The solution to matrix equation AX+XTC=B［J］. Journal of the Franklin Institute，2007，344：1056－1062.

［4］ Xie L，Liu Y J，Yang H Z. Gradient based and least squares based iterative algorithms for matrix equation AXB+CXTD=E［J］. Applied Mathematics and Computation，2010，217：2191－2199.

［5］ Wang M H，Cheng X H，Wei M S. Iterative algorithms for solving the matrix equation AXB+CXTD=E［J］.Applied Mathematics and Computation，2007，187（2）：622－629.

［6］ Teran F，Dopico F. The solution of the equation XA+AXT=0 and its applications to the theory of orbits［J］.Linear Algebra Appl，2011，434：44－67.

［7］ 赵琳琳. 矩阵方程AXB+CXTD=E 的可解性［J］. 山东大学学报：理学版，2012，47（10）：45－48.

［8］ Dehghan M，Hajarian M. Finite iterative algorithms for the reflexive and anti－reflexive solutions of the matrix equations A1X1B1=C，A2X2B2=D［J］. Mathematical and Computer Modeling，2009，49：1937－1959.

［9］ 盛兴平，苏友峰，陈果良. 矩阵方程ATXB+BTXTA=D 的极小范数最小二乘解的迭代算法［J］. 高等学校计算数学学报，2008，30（4）：352－362.

［10］孙合明，李庆芳，杨家稳. 自反矩阵下矩阵方程AXB+CXD=E 的最佳逼近解［J］. 重庆理工大学学报：自然科学，2012，26（4）：109－114.

［11］Yamada I. The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings［M］//Butnariu D，Censor Y，Reich S. Inherently parallel algorithm for feasibility and optimization and their applications.Amsterdam：Elsevier，2001：473－504.

［12］Yamada I，Ogura N，Shirakawa N. A numerically robust hybrid steepest descent method for the convexly constrained generalized inverse problems［J］. Contemporary Mathematics，2002，313：269－305.