飞秒激光场中μ子催化聚变的轨迹分析

苏 晋，石春花，袁小燕

（长治医学院 a.基础医学部物理教研室； b.生物医学工程系，山西 长治 046000）

自20世纪80年代发现 μ介子（简称 μ子，符号 μ代表的就是带负电的介子 μ-）催化氘-氚混合物（d-t）在室温下产生超过100次的核聚变反应［1］以来，大量的科研工作者开始探讨 μ子催化核聚变反应（μCF）的内在物理机制，并试图利用其进行高效的能源生产［2］，关于此项研究已经在实验和理论上取得了不少成果［3-5］。然而，这一系列的研究同时也表明，每进行一次μCF，反应结束后，作为催化剂的 μ子有可能被3He（α粒子）捕捉形成(αμ)+，从而不能参加下一轮的催化反应，使得实现能源生产存在一定困难。因此，μCF中的粘附现象成为了聚变反应中的探讨热点之一［6-7］。目前，有工作组在实验室已经可以在μ子的半衰期（约2.2×10-6s）里观察到超过150次的聚变反应［8］。

本文从μ子催化核聚变反应的产物出发，以氘-氘（d-d）聚变为研究对象，当一次催化聚变完成后，反应关系式之一为

μ+d+d→ddμ→α+n+μ，

由于反应产物中各种粒子的束缚能级能量不同，将有一部分 μ子被束缚（粘附）在反应产物3He上，失去了再次催化的能力，即

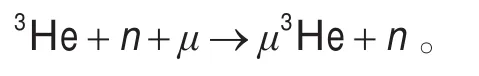
为了提高μ子的催化次数，笔者试图借助飞秒激光场的作用，探讨μ子在激光场中的轨迹，使得被3He所俘获的μ子摆脱束缚再生，其再生反应为

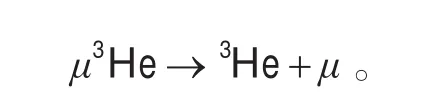
当d-d聚变完成一轮，μ子尚未被捕获时，此刻反应产物中会形成多粒子存在的混合状态，其中包括 μ子、α粒子、中子n、氘粒子d、电子e，笔者试图将这一混合状态看作一种等离子体，假设这一等离子体的频率为ωp，那么，

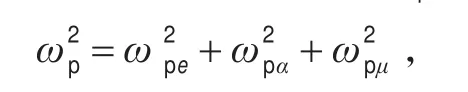
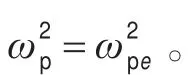
1 模型的建立

为了研究方便，选择线偏振飞秒脉冲激光，坐标轴X轴作为脉冲激光的传播方向，坐标轴Y轴代表激光束电场强度的方向，坐标轴Z轴代表其磁场强度的方向。激光脉冲开启和结束时，选择激光的形状为高斯状，即激光电场强度随时间变化的式子为

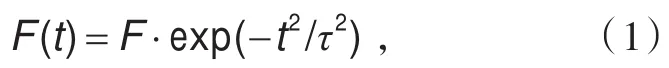
其中τ是激光脉冲的周期，ωτ＞＞1。

对于d-d聚变的反应产物来说，x=0代表稠密等离子体的表面，x＞0代表稠密等离子体的内部深度。因此，线偏振激光垂直进入到靶或者说稠密等离子体的表面，此时，激光场的电场强度和磁场强度的边界条件可以用以下式子表示：

利用牛顿经典方程，μ子在混合体内（x＞0）与激光接触后，产生的速度在X轴和Y轴的分量分别为（这里采用单位：me=c=e=1，其中me为电子的质量，c为光速，e为电子的电量）。

其中 k=mμ/me≈207，δ=c/ωp=1/ωp为深入等离子内部的距离。假设x=0代表靶的表面。μ子的运动在磁场方向上没有分量，即μ子的运动不沿着Z轴方向。除此之外，μ子彼此间的碰撞在这里也不考虑，那么，利用初始条件方程（4）就可以进行数值求解，初始条件为

2 数值计算

经过（4）式和（5）式的计算可知，μ子的运动仅由 f=2F/ω和ωp/ω两个参数决定。其中参数f=1代表激光电场的峰值强度为5×1017W/cm2（激光光子的能量ћω=1.5eV）。为了计算的方便，设置参数 ωp/ω =7，ωτ/2π =30，脉冲周期τ=83 fs，电子密度为 ne=8× 1022cm-3。

基于上述的参数设定，（4）式的求解结果如图1所示，这里笔者选择的参数 f=100（激光电场的峰值强度为5×1021W/cm2），纵坐标的单位为光速c。与图2相比较，可以很明显看到，在激光脉冲的能量达到最大之前（当ωt=-250处），μ子在X轴上的速度分量已经不再增加，即停止了加速，而由于等离子体的厚度，即x的值很小，所以基本肯定在激光脉冲的能量达到最大之前，μ子已经到达等离子体的最深处，完成了自由状态的转变，并且，由于激光脉冲的绝热性，当μ子离开表层时，它的速度趋于0。

图1 μ子在X轴、Y轴上的速度分量随激光相位的变化

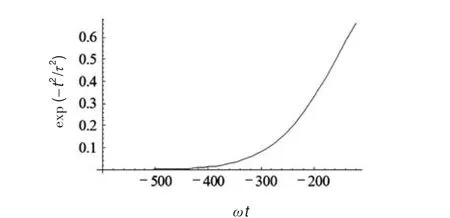
图2 激光的电场强度随相位的变化

为了更进一步说明μ子在等离子体内的自由穿越，依据（4）式的解，做出了 μ子在激光作用下的轨迹图，图3表示激光参数 f=100时，μ子在等离子体内部的轨迹，其中坐标轴 X和Y以传播深度δ为单位，从图3可以明显看出，μ子在Y轴上发生振荡，振幅为0.0025δ，而 μ子在 X轴上有约0.4δ的移动距离，可以说，μ子在Y轴上振荡的振幅远远小于漂移运动，而漂移运动恰恰指的是 μ子在 X轴方向上发生移动，此方向也是脉冲激光的传播方向。因此，可以得出结论，在激光脉冲的峰值达到最大之前，μ子已经穿过等离子体的表面，达到深处，直至变成自由状态。

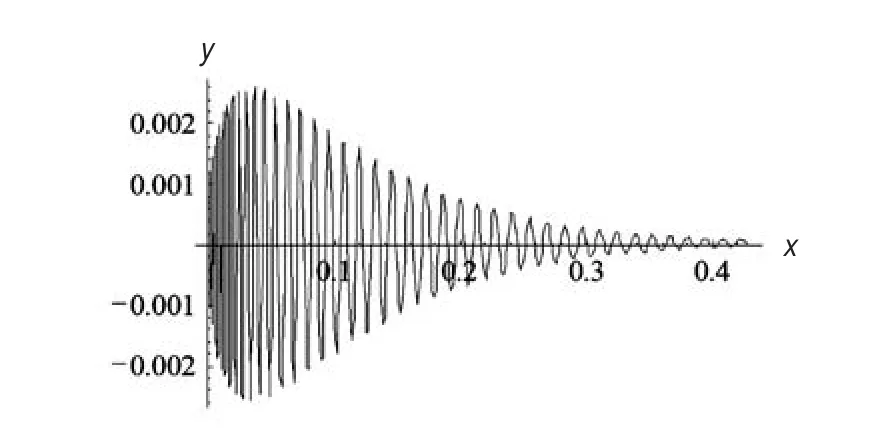
图3 μ子的轨迹

3 结果与讨论

最后定量描述一下笔者得到的结论，假设μ子沿着激光传播方向的漂移速度为vx=va，其中va是μ子漂移的平均速度，时间tp为穿透等离子体表面进入内部深度为 x（x=xmax）所用的时间，这样，我们可以近似的表示为

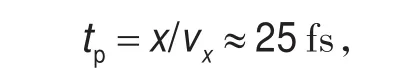
tp≈25fs＜τ，也就是说，μ子从完成第一轮的催化反应后，存在于聚变产物中，由于激光场的介入，它脱离了α粒子束缚，按照激光的照射方向，变成自由粒子，而从聚核产物的出现到μ子穿透稠密等离子体变成自由粒子所需的时间远远少于激光的脉冲周期，因此可以说，合适激光场的作用，使得μ子可以快速的变成自由状态，重新进行下一轮的催化聚变。

另外，由于激光的介入，也必须考虑激光对稠密等离子体中除μ子外其他带电粒子的影响。基于相似的方法，笔者讨论了其他带电粒子的轨迹，当然，均是在相同的激光参数进行的数值计算，即取 f=100。结果表明，由于其他粒子具有不同的初速度，但是这个初速度非常小，甚至可以忽略不计，因此，激光对它们的影响自然也是很小的。也就是说，与 μ子相比，在激光场中，这些粒子的运动也是很小的。更进一步说，激光的周期如此短暂，以至于它不会给 μCF的反应带来不利，却可以避免α粒子对 μ子的粘合。

总之，基于脉冲激光场中μ子轨迹的分析发现，μ子在激光的介入下，从混合层的一侧穿到另一侧，即从混合产物组成的稠密等离子体中脱离出来，所需的时间远远小于激光的脉冲周期τ。因此，在 μCF（d-d）反应完成之时，加入适当的激光场，在 μ子尚未被α粒子捕获时，它就会随着激光的传播方向发生较大的漂移，且时间极短，穿透等离子体，变成自由粒子，重新进行下一轮的聚变催化，且不影响整个反应的发生，一定程度上提高了催化效率。

［1］Gershteǐn S S，Petrov Y V，Ponomarev L I.Muon catal⁃ysis and nuclear breeding［J］.Sov Phys Usp，1990，33（8）：591-615.

［2］Alexander S A，Froelich P，Monkhorst H J.Nuclear fu⁃sion rates of muonic molecular ions［J］.Phys Rev A，1990，41（5）：2854-2857.

［3］Gheisari R.An optimized hydrogen target for muon cata⁃lyzed fusion［J］.Nuclear Instruments and Methods in Physics Research Section A：Accelerators，Spectrome⁃ters，Detectors and Associated Equipment，2011，634（1）：1-4.

［4］Kawamura N，Ishida K，Matsuzaki T，et al.Muonic molecule formation in muon-catalyzed fusion［J］.Jour⁃nal of Physics：Conference Series，2010，225（1）：012025.

［5］许声毓.“氧核冷裂变”或可改变世界的新能源技术革命［J］.中国科技财富，2010（11）：12-20.

［6］Nagamine K，Ponomarev L.Recent progress in muon catalyzed fusion［J］.Nuclear Physics A，2003，721：C863-C866.

［7］Ishida K，Nagamine K，Matsuzaki T，et al.Muon cata⁃lyzed fusion［J］.NuclearPhysicsB，2005，149：348-350.

［8］何景棠.和2002年诺贝尔物理学奖有关的一段史实［J］.物理，2003，32（8）：560-562.

［9］Rastunkov V S，Krainov V P.Electron stochastic heat⁃ing in the interaction of a short laser pulse with over⁃dense plasma［J］.Laser Physics， 2005，15（2）：262-267.